Механизм мономолекулярных реакций по теории активных столкновений (схема Линдемана)

Формальная кинетика предполагает, что порядок реакции зависит от молекулярности самой медленной стадии. Согласно теории активных столкновений химическая реакция начинается с соударения двух (значительно реже - трех) молекул. Так как большая часть реакций имеет первый порядок, то это означает, что реакция не ограничивается только столкновением двух частиц.

Механизм реакции, объясняющий появление первого порядка при столкновении двух молекул, был предложен Линдеманом в 1922 г. и называется схемой Линдемана.

Согласно этой схеме столкновение двух молекул не приводит к мгновенному химическому превращению, а его результатом является перераспределение энергии молекул в момент удара и образование частицы с избыточной энергией А*:

k₁

А + А ¾® А* + А. (I)

Частица с избыточной энергией А* (ее можно также называть возбужденной молекулой) способна претерпевать дальнейшее превращение до продукта В:

k₂

А* ¾® В. (II)

Кроме того, сталкиваясь с другими частицами, активная частица А* может вернуть избыток энергии и вернуться в исходное состояние:

k _-1

А* + А ¾® А + А. (III)

Всю совокупность реакций можно представить следующим образом: k₁

А + А D А* + А. (IV)

k _-1 ¯ k₂

В

Скорость накопления активных частиц в соответствии с этой схемой описывается уравнением:

(12 - 20)

Зависимость концентрации активных частиц от времени с начала реакции показана на рис. 12 - 2.

Как видно из рис. 12 - 2, вначале концентрация активных частиц в течение короткого времени очень быстро возрастает, затем в течение длительного времени медленно уменьшается. Производная концентрации по времени до точки максимума по абсолютной величине может во много раз превышать производную концентрации по времени после точки максимума. В связи с этим, сравнивая производную после достижения максимума с производной на начальном участке кривой, можно для убывающей части кривой принять:

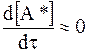. (а)

Условие (а) называется квазистационарным состоянием.

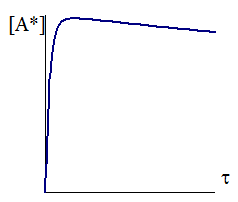Рис. 12 - 2. Изменение концентра­ции промежуточного вещества со временем.

При квазистационарном состоянии уравнение (12 - 20) принимает следующий вид:

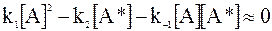. (12 - 21)

Решение уравнения (12 - 21) относительно концентрации активных частиц дает:

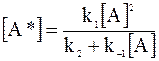. (12 - 22)

Скорость образования вещества В характеризуется уравнением:

или

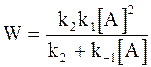. (12 - 23)

Если константа скорости k₂ окажется достаточно большой, чтобы выполнялось условие k₂ >> k₋₁[A], то уравнение (12 - 23) превращается в уравнение скорости реакции второго порядка:

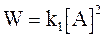. (12 - 24)

В случае очень малой константы k₂ выполняется условие: k₂ << k₋₁[A], а уравнение (12 - 23) превращается в уравнение скорости реакции первого порядка:

. (12 - 25)

Полученные результаты легко объяснимы.

Если скорость превращения активной частицы очень велика, то она существует крайне непродолжительное время и не успевает сталкиваться с другими частицами. В этом случае скорость реакции определяется только стадией (I) и реакция является бимолекулярной.

Если частица, не превращаясь, существует в течение длительного времени, то велика вероятность ее столкновения с другими частицами. В этом случае скорость реакции возрастает вместе с увеличением скорости накопления промежуточных активных частиц и скорости их превращения в продукты реакции и убывает с ростом скорости превращения активных частиц в исходные неактивные.

Схема Линдемана подтверждается данными, полученными при изучении реакций в газовых фазах.

При очень низких давлениях газа столкновения активных частиц с другими молекулами происходят редко и они успевают превратиться в продукты реакции. В этом случае следует ожидать второй порядок реакции. При высоких давлениях частота столкновений возрастает и полностью выполняется условие: k₂ << k₋₁[A], а реакция описывается уравнением (12 - 15). Опыт показал, что проводя реакцию от давлений в несколько сотых мм рт. ст. (от нескольких Па) до десятков атмосфер (несколько МПа), можно наблюдать переход от кинетики реакции второго порядка до реакции первого порядка.