Закони розподілу випадкових похибок.

Рівномірний розподіл. Якщо похибка вимірювання може мати з однаковою ймовірністю які завгодно значення, що не виходять за деякі межі ± Δ_n, то така похибка описується рівномірним законом розподілу. При цьому щільність ймовірності похибки р(Δ) є постійною всередині цього інтервалу і дорівнює нулю поза ним.

Рівномірний розподіл результатів спостереження х показаний на рис. 5.

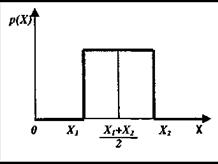
Рис. 5 Рівномірний розподіл випадкової величини

Для нього щільність ймовірностей аналітично можна записати так:

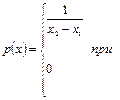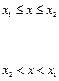
(3.19)

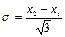Рівномірний розподіл є безмодальним, тобто не має моди, його дисперсія і середньоквадратичне відхилення , а четвертий момент 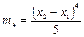та контрексцес

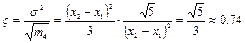
З таким законом розподілу добре узгоджуються похибки від тертя в опорах електромеханічних приладів, невилучені залишки систематичних похибок, похибка дискретності в цифрових приладах, похибки розмірів в межах однієї групи сортування при селективному збиранні, похибки параметрів виробів, відібраних у вужчих, ніж технологічний допуск, межах.

Закон трикутного розподілу (закон Сімпсона). Вигляд кривої трикутного розподілу маємо на рис. 6. За таким законом розподілені похибки суми (різниці) двох рівномірно розподілених величин.

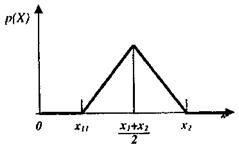
Рис. 6 Диференційна функція трикутного розподілу

Щільність ймовірностей має такий аналітичний вираз:

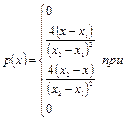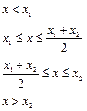
(3.20)

Трапецієподібний закон розподілу. Вигляд цього розподілу показаний на рис. 7. Похибка має такий закон розподілу, якщо вона утворюється з двох незалежних складових, кожна із яких має рівномірний закон розподілу, але з різною шириною своїх інтервалів. При послідовному з'єднанні двох вимірювальних перетворювачів, один із котрих має похибку, рівномірно розподілену в інтервалі ±Δх₁, а інший – похибку, рівномірно розподілену в інтервалі ±Δх₂, загальна похибка перетворення буде опи­суватись трапецієподібним законом розподілу. Трикутний закон розподілу є частковим випадком трапецієподібного, коли Δх₁ = Δх₂.

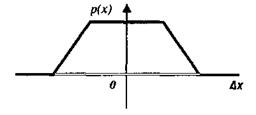
Рис. 7 Диференційна функція трапецієподібного закону

розподілу похибок

Ці три закони розподілу мають обмежене застосування при оцінюванні ре­зультатів вимірювань, оскільки переважно похибки виникають через вплив великої кількості причин. У таких умовах розподіл похибок найкраще узгоджується з нормальним законом розподілу.

Нормальний закон розподілу (закон розподілу Гаусса). Цей закон є одним із найпоширеніших законів розподілу похибок, що пояснюється центральною граничною теоремою теорії ймовірностей, яка твердить, що розподіл випадкових похибок буде близьким до нормального, якщо результати спостереження формуються під впливом великої кількості незалежних факторів впливу, кожний із котрих створює лише незначну дію порівняно з сумарною дією всієї решти.

Нормальний закон має такий вираз для диференційної функції розподілу:

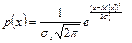
(3.21)

із рівняння можна зробити висновок:

1. Густина ймовірностей має максимум при х = М[х];

2. Із збільшенням похибки Δ = х – М[х] незалежно від знака (функція парна) густина ймовірності прямує до нуля;

3. Із збільшенням середнього квадратичного відхилення ймовірність більших відхилень зростає, тобто розміри розсіюються в ширшому інтервалі.

Необхідно зауважити, що незважаючи на широке застосування нормального розпо­ділу, він все-таки є лише моделлю реальних розподілів. До речі, він відмінний від нуля вздовж всієї нескінченності осі. Тому нормально розподілена випадкова величина, хоч із малими ймовірностями, але може приймати які завгодно великі значення. Хоча очевидно, що всі вимірювані фізичні величини завжди обмежені за абсолютним значенням.

Графічно ця функція показана на рис. 8 для різних значень середнього квадратичного відхилення (σ₁ < σ₂).

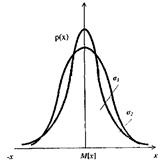
Рис. 8 Диференційна функція нормального розподілу похибок

Функція розподілу нормальної випадкової величини має такий вигляд:

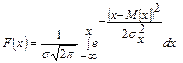
(3.22)

Крива розподілу буде змінюватись залежно від середнього квадратичного відхилення. Але якщо виразити похибку деяким числом і середніх квадратичних відхилень, то отримаємо криву нормованого розподілу з аргументом

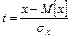
(3.23)

яка описується таким виразом:

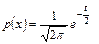
(3.24)

Як відомо, цей вираз нормованої функції отриманий за умови, що .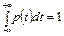

Інтегральна функція нормального нормованого розподілу має такий вигляд:

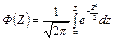
(3.25)

де аргумент z визначається, як і для t, діленням відхилення випадкової величини від математичного сподівання на середнє квадратичне відхилення

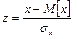
(3.26)

Вигляд інтегральної функції нормального розподілу показано на рис. 9.

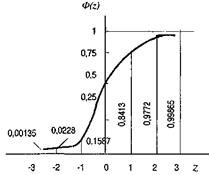
Рис. 9 Інтегральна функція нормального розподілу

Значення Ф(І) визначаються із таблиці (додаток ..., табл. ...).

Розподіл Релея. Цей розподіл має модуль двовимірного вектора, координати котрого розподілені нормально відносно нульових математичних сподівань і однако­вих дисперсій

(3.27)

Розподіл Релея зручний для апроксимації розподілу контрольованих показників, котрі можуть бути лише з однаковим знаком. Наприклад, при контролі відхилення форми і розміщення осей та поверхонь деталей, як овальність, конусність, радіальне биття, відхилення від співосності, паралельності, перпендикулярності тощо можна описати тільки таким розподілом.