Вимірювання
Визначення статистичних параметрів розподілу на підставі побудови гістограми. У звичайних умовах параметри розподілу визначаються за допомогою математичного опрацювання обмеженої кількості результатів спостережень, званої вибіркою. Множина результатів спостережень, з котрих зроблено вибірку, називається генеральною сукупністю результатів спостережень. При атестації засобів вимірювання виконують обмежену кількість вимірювань одного і того ж розміру, котру також називають вибіркою. Генеральною сукупністю в цьому випадку буде множина розмірів, які можна було б отримати даним вимірювальним засобом при дотриманні умов вимірювання, вказаних в інструкції з експлуатації засобу вимірювання.
Розглянемо як будуються емпіричні криві розподілу. Нехай об'єм вибірки становить п, найменший розмір хтіп, найбільший – хмах. Для побудови емпіричних кривих розподілу необхідно розбити весь отриманий діапазон хтах - хтіп на r інтервалів.
Кількість інтервалів при великих вибірках доцільно брати округленим 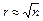 . При великих вибірках кількість інтервалів встановлюють залежно від кількості спостережень за такими рекомендаціями:
. При великих вибірках кількість інтервалів встановлюють залежно від кількості спостережень за такими рекомендаціями:
| п | r |
| 40-100 | 7-9 |
| 100-500 | 8-12 |
| 5000-10000 | 10-16 |
Довжину інтервалів зручніше вибрати однаковою. Але якщо розподіл має раптові стрибки в сусідніх інтервалах, то в області максимальної концентрації результатів спостережень належить вибирати вужчі інтервали. Ширина інтервалу має бути зручною для графічних робіт відносно поділок вздовж осі х. Нижню межу першого інтервалу не варто брати такою, як xmіп якщо вона не відповідає зручному положенню на осі х. При опрацюванні результатів потрібно надати перевагу відхиленням розмірів, а не розмірам (для зменшення помилок при обчисленнях). Особливо великі помилки виникають при обчисленні моментів другого та вищих порядків.
Кількість розмірів т, що попали в заданий і-й інтервал за умовою
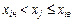
| (5.1) |
називається абсолютною частотою. У нерівності (5.1) хj є результатом j-го спостереження вибірки, в якій 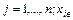 – верхня межа i-го інтервалу; хін – нижня межа і-го інтервалу, яка дорівнює верхній межі (і - 1)-го інтервалу. Необхідно звернути увагу на те, що сума частот ті має дорівнювати кількості п, тобто
– верхня межа i-го інтервалу; хін – нижня межа і-го інтервалу, яка дорівнює верхній межі (і - 1)-го інтервалу. Необхідно звернути увагу на те, що сума частот ті має дорівнювати кількості п, тобто
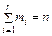
| (5.2) |
Відношення абсолютної частоти ті до загальної кількості спостережень п називають відносною частотою і позначають
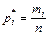
| (5.3) |
Відносна частота становить емпіричну оцінку ймовірності попадання результатів спостереження хj в j-й інтервал. Очевидно, що
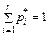
| (5.4) |
Для наочності емпіричний розподіл подають графічно у вигляді полігона, гістограми розподілу або ступінчастої функції розподілу.
Полігон будується так: на осі абсцис відкладають інтервали значень вимірюваної величини, в середині кожного із інтервалів відзначають ординати, пропорційні до частот і ординати з'єднують прямими лініями. Вибираючи масштаби вздовж осей абсцис та ординат дотримуються співвідношення ≈5:8, яке є найпоширенішим при зображенні кривих розподілу.
Гістограму будують так: над кожним інтервалом вздовж осі абсцис будують прямокутник, площа котрого пропорційна до відносної частоти 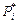 в цьому інтервалі, а висота буде пропорційною до абсолютної частоти при однакових інтервалах. При різних значеннях Δх висота прямокутника буде пропорційною до емпіричної щільності ймовірностей
в цьому інтервалі, а висота буде пропорційною до абсолютної частоти при однакових інтервалах. При різних значеннях Δх висота прямокутника буде пропорційною до емпіричної щільності ймовірностей

| (5.5) |
Ступінчасту функцію розподілу будують так: в середині кожного інтервалу вздовж осі абсцис ордината зростає стрибком на значення, що відповідає 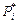 , і звідти проводять горизонтальну пряму до середини наступного інтервалу, де ордината знову зростає. Висота ординати в кожній точці відповідає емпіричній інтегральній функції розподілу.
, і звідти проводять горизонтальну пряму до середини наступного інтервалу, де ордината знову зростає. Висота ординати в кожній точці відповідає емпіричній інтегральній функції розподілу.
Виявлення грубих похибок. Відомо, що грубими похибками називаються похибки, які значно переважають похибки, обґрунтовані умовами експерименту. Вважаємо, що всі результати спостереження мають однакову дисперсію. Проте окремі результати можуть видатися експериментатору підозрілими. Необдумане відкидання цих результатів може спотворити оцінку параметрів дійсного розподілу. Якщо експериментатор зауважив результат, що видався йому неправильним, і, крім того, знайшов причину промаху (помилкова дія, відчитування тощо), то він може відкинути цей результат і провести додаткові вимірювання. Якщо причина не вияснена, то додаткові вимірювання належить провести, але відкидати підозрілий результат без перевірки статистичними методами не можна.
В такому разі припускають, що результат спостереження хі не містить грубої похибки, тобто є одним із значень випадкової величини х, розподіленої за законом 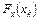 , параметри якого попередньо визначені.
, параметри якого попередньо визначені.
Підозрілими можуть бути або хтіп, або хтах із всієї низки спостережень, тому для перевірки гіпотези визначають величину v.
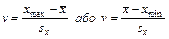
| (5.6) |
Розподіли цих величин наведені в табл. Д.5 (додаток 12). [1]. За цією таблицею можна визначити граничне значення va, котре при заданій вірогідності a і даній кількості спостережень, випадкова величина v може прийняти випадково. Якщо обчислене за дослідними даними значення v виявиться меншим, ніж va, то гіпотеза приймається. В іншому випадку гіпотеза відхиляється, результат спостереження розглядається як такий, що містить грубу похибку і відкидається. Природно, що при цьому можливими є помилки першого і другого видів, оскільки припущення перевіряється при деякому рівні значущості 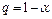 .
.
Критерій нехтовних похибок. Правила округлень. При опрацюванні результатів спостережень всі проміжні обчислення треба виконувати, зберігаючи необхідну кількість значущих цифр і правильно округлювати результати і похибки вимірювань. Похибка результату вимірювання має бути виражена однією або двома значущими цифрами. Найменші розряди числових значень результату і похибки вимірювання мають бути одні і ті ж самі. Двома значущими цифрами похибка виражається: при точних вимірюваннях і коли в старшому розряді її числового значення стоїть цифра, не більша за три.
Похибку проміжних обчислень треба виражати не більше ніж трьома значущими цифрами. Значущих цифр у результатах проміжних обчислень має бути на одну-дві більше ніж у числовому значенні результату вимірювання. При такій умові похибки обчислень не спотворять числового значення результату вимірювання більше, ніж на половину одиниці найменшого розряду.
Результат вимірювання треба округлювати за такими правилами.
1. Найменший розряд числового значення округленого результату вимірювання повинен бути той самий, що й останній розряд числового значення похибки вимірювання. Наприклад, 53,0138 при числовому значенні похибки 0,05 округлюється до 53,01.
2. Якщо перша (зліва направо) із цифр, що замінюються нулями (цілі числа) або відкидаються (десятковий дріб), менша за 5, то збережені цифри залишають без зміни. Наприклад, якщо треба зберегти три значущих цифри, то 123429 округлюється до 123×103, а 12,3429 – до 12,3.
3. Якщо перша із цифр, що замінюється нулями або відкидається, менша за 5, то роблять округлення до парного числа (якщо остання цифра парна, то вона залишається без зміни, а якщо непарна, то збільшується на одиницю). Наприклад, якщо треба зберегти три значущі цифри, то 35450 округлюється до 354×102, а 145,5 – до 146.
4. Якщо перша із цифр, що замінюються нулями або відкидаються, не менша за 5 і після неї йдуть цифри, відмінні від нуля, то останню цифру збільшують на одиницю. Наприклад, якщо треба зберегти три значущі цифри, то 12560 округлюється до 126×102, а 30,651 – до 30,7.
Отже, найбільша відмінність в двох значущих цифрах, яка може бути при округленні, становить 5%.
При визначенні сумарної похибки випадкових похибок результат отримується за формулою
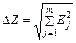
| (5.7) |
Якщо при цьому одна із часткових похибок дає величину 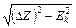 , для котрої справедливим є
, для котрої справедливим є
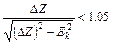
| (5.8) |
то такою похибкою можна знехтувати, бо отримана відмінність при округленні губиться, оскільки число 1,0499 приймається як 1. Звідси витікає умова
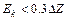
| (5.9) |
Ця формула називається критерієм нехтовних похибок, а самі похибки називаються нехтовними чи нехтовно малими. При великій кількості похибок за критерієм нехтовних похибок оцінюються суми квадратів часткових похибок
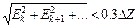
| (5.10) |
Використання критерію нехтовних похибок при аналізі часткових похибок дає можливість виділити ті величини, які суттєво впливають на похибку результату. Підвищення точності вимірювання цих величин дозволить зменшити сумарну похибку. Крім цього, можна навіть знизити точність тих вимірювань, похибки котрих мізерні, але, річ ясна, тільки тоді, коли це економічно доцільно.
Дата добавления: 2015-08-26; просмотров: 1229;
