Засоби вимірювань та їх метрологічні характеристики. Класифікація засобів вимірювань. Статистичний аналіз і оцінка похибок вимірювань.

Поняття і види засобів вимірювальної техніки. Основою технічної бази метрологічного забезпечення є засоби вимірювальної техніки. Засобами вимірювальної техніки називають технічні засоби, які викорис­товуються при вимірюваннях і мають нормовані метрологічні характеристики. Метрологічними називаються ті характеристики ЗВТ, від яких залежить точність ре­зультатів, одержаних за їх допомогою. Нормування метрологічних характеристик полягає в законодавчому регламентуванні їх складу і норм значень.

Під видами ЗВТ розуміємо: міри, їх набори і магазини, вимірювальні пере­творювачі, прилади, установки і системи.

Міра – ЗВТ, що призначені для відтворення ФВ заданого розміру (однозначна міра) або ряду розмірів (багатозначна міра).

Набір мір – це спеціально підібраний комплекс конструктивно відокремлених мір, які можна використовувати не тільки окремо, але й у різних комбінаціях для відтворення ряду розмірів даної ФВ, наприклад набір гир, вимірювальних резисторів, конденсаторів, Набір мір, конструктивно об'єднаних в одне ціле з пристроєм для вмикання їх у різних комбінаціях, називається магазином мір. Наприклад, магазин опору, ємності, індуктивності.

Вимірювальний перетворювач – ЗВТ, що призначений для перетворення вхідного вимірювального сигналу на вихідний сигнал, який зручний для подальшого пере­творення, обробки, зберігання чи передавання вимірювальної інформації, але не для безпосереднього сприймання спостерігачем. Наприклад, калібрований шунт, вимірю­вальний трансформатор, атестована термопара.

Вимірювальний прилад – ЗВТ, вихідний сигнал якого придатний для без­посереднього сприймання вимірювальної інформації спостерігачем, завдяки наявності відлікового пристрою (шкала з вказівником, цифрове табло). Наприклад: вольтметр, ватметр, термометр. Вимірювальні перетворювачі і прилади об'єднують спільною назвою – вимірювальні пристрої.

Вимірювальна установка – сукупність функціонально об'єднаних ЗВТ (мір, вимірювальних пристроїв) і допоміжних технічних засобів (стабілізуючих, перемикаючих), розташована в одному місці і призначена для одержання вимірювальних сигналів, придатних для безпосереднього сприймання вимірювальної інформації спостерігачем. Наприклад, установка для випробувань феромагнітних матеріалів, для вимірювання питомого електричного опору електротехнічних матеріалів.

Вимірювальна система – сукупність ЗВТ і допоміжних пристроїв, що з'єднані каналами зв'язку, призначена для вироблення сигналів у формі, придатній для автоматичної обробки, передавання і (або) використання вимірювальної інформації в автоматизованих системах управління. Вимірювальні системи є різновидом інфор­маційно-вимірювальних систем (ІВС), до яких належать також системи автоматичного контролю, технічної діагностики, розпізнавання образів. ІВС входять до складу автоматизованих систем управління.

Класифікація вимірювальних приладів. Серед усіх видів ЗВТ найбільшого поширення набули вимірювальні прилади. Вони різноманітні за призначенням, принципом дії, метрологічними та експлуатаційними характеристиками. Тому їх можна класифікувати за багатьма ознаками, але з погляду подальшого викладу доцільно обмежитись розглядом найзагальніших класифікацій­них ознак.

За формою вимірювальної інформації, що міститься в інформативному параметрі вихідного сигналу, вимірювальні прилади поділяються на аналогові та цифрові. Аналоговим називається прилад, інформативний параметр вихідного сигналу якого є фізичним аналогом вимірюваної величини – інформативного параметра вхідного сигналу. Наприклад, переміщення рухомої частини електродинамічного вольтметра –аналог середнього квадратичного значення вимірювальної напруги.

Цифровим називається прилад, вихідний сигнал якого цифровий, тобто містить інформацію про значення вимірюваної величини, закодовану в цифровому коді. Покази аналогових приладів також цифрові, але їх аналогові вихідні сигнали квантує і кодує у цифровому коді сам спостерігач (експериментатор) під час відліку показів, а в цифровому приладі - операції виконуються автоматично.

Вимірювальний прилад, що допускає тільки відлік показів, називається пока­зуючим, а прилад, в якому передбачена автоматична фіксація вимірювальної інфор­мації, – реєструючим. Залежно від виду фіксації реєструючі прилади поділяються на самописні та друкуючі. Самописний прилад (самописець) записує вимірювальну інформацію в аналоговій формі у вигляді діаграми, а друкуючий друкує вимірювальну інформацію в цифровій формі.

Залежно від виду значення вимірюваної величини, тобто інформативного параметра вхідного сигналу, відрізняють прилади миттєвих та інтегральних (середнє за модулем, середнє квадратичне) значень, а також інтегруючі та підсумовуючі прилади. Інтегруючий прилад інтегрує вхідний сигнал за часом або іншою незалежною змінною. Наприклад, лічильник електричної енергії інтегрує миттєву потужність за часом. Підсумовуючим називається прилад, покази якого функціонально пов'язані з сумою двох або декількох величин, що підводяться до нього різними каналами, наприклад ватметр для вимірювання потужності декількох генераторів.

Класифікаційними ознаками вимірювальних приладів служать вимірювана ве­личина або її одиниця, що відображаються в назві вимірювального приладу, наприклад, вологомір або гігрометр, висотомір або альтметр, частотомір або герцметр, вольтметр, мілівольтметр тощо.

Електровимірювальні прилади, що дозволяють вимірювати дві і більше різних за фізичною природою величини, називають комбінованими приладами або мультиметрами, а прилади, що придатні для вимірювань у колах постійного і змінного струмів – універсальними приладами.

Похибки вимірювань та їх види. Кількісний вміст властивості, що відображається фізичною величиною, визначається розміром фізичної величини. Ще до вимірювання існує деякий розмір фізичної величини, котрий можна би було оцінити відповідним числовим значенням. Це значення називають істинним.

Істинне значення фізичної величини – це значення, що ідеально відображає властивості даного об'єкта як кількісно, так і якісно. Воно є об'єктивним і не залежить ні від нашої свідомості, ні від технічних засобів, що застосовуються при експери­ментальному його визначенні. При експериментальному визначенні значення фізичної величини завжди будемо отримувати значення величини, відмінне від істинного, бо завжди існує похибка вимірювання.

Абсолютною похибкою вимірювання Δ називають відхилення результату вимі­рювання від істинного значення вимірюваної величини

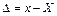
(3.1)

Абсолютна похибка не може служити мірою точності, бо, наприклад Δ = 0,5 мм при х = 100 мм є достатньо малою, але при х = 1.0 мм – вона дуже велика. Тому вводиться поняття відносної похибки:

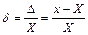
(3.2)

де х – результат вимірювання; X – істинне значення вимірюваної величини.

Дійсне значення вимірюваної величини це є її значення отримане експери­ментально, і настільки наближене до істинного, що для даної мети його можна використати замість нього.

Оскільки істинне значення вимірюваної величини невідоме, то практично знаходять наближені значення абсолютної і відносної похибок вимірювання:

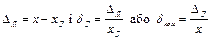
де х_Д – дійсне значення вимірюваної величини (має бути відоме з похибкою, що в кілька разів менша за похибку Δ_Д).

Зрозуміло, що легше знайти похибку d_ном, яка називається номінальною від­носною похибкою і, якщо вона невелика, то мало відрізняється від d_д.

Похибка вимірювання зумовлена, переважно, наявністю похибок засобів вимі­рювання і є результуючою похибкою багатьох складових, кожна з яких викликана певною причиною. Розрізняють чотири групи похибок.

Інструментальні – похибки, зумовлені недосконалістю засобів вимірювань.

Похибки установлення – це похибки, спричинені неправильним установленням засобу вимірювань, впливом відхилень умов виконання вимірювального експерименту від тих, що були при градуюванні засобу вимірювань.

Похибки методу вимірювання – спричинені недосконалістю цього методу, не­достатньою обґрунтованістю його теорії, застосуванням наближених формул для спрощення розрахунків тощо.

Особисті похибки – виникають переважно при відлічуванні показів. Причини їх ви­никнення: недосконалість зору оператора, втомленість, схильність занижувати або зави­щувати відлік, округляти до парних або непарних цифр тощо.

Похибки трьох перших груп називають об'єктивними, а похибки четвертої групи – суб'єктивними. Об'єктивні похибки можуть виникати на довільній стадії вимірювальних пере­творень, а суб'єктивні – тільки при відчитуванні показів експериментатором.

У реальних умовах усім величинам, зокрема й похибкам, властива певна невизначеність, мірою якої характеризується їх випадковість. Залежно від закономірності проявлення похибки ділять на систематичні, випадкові і грубі.

Систематичною похибкою – називається складова похибки вимірювання, яка залишається сталою або закономірно змінюється при повторенні вимірювань однієї і тієї самої величини.

Випадкова похибка – це та складова похибки, яка при повторенні вимірювань величини з незмінним розміром змінюється випадково.

Груба похибка – це похибка вимірювання, яка істотно перевищує сподівану за даних умов вимірювання похибку.

Чим менші систематичні і випадкові похибки, тим вища точність вимірювання. Тому точність вимірювання є характеристикою їх якості і показує близькість результатів вимірювання до істинного значення вимірюваної величини.

Кількісною оцінкою точності вимірювань є число, обернене до відносної похибки (запропоновано у 1955 р. Соловйовим М.М.)

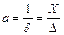
(3.3)

Характеристикою якості вимірювання, яка відображає близькість систематичної похибки до нуля, є правильність вимірювання. Коли систематична похибка відома, то результат можна виправити введенням поправки.

Поправка – значення абсолютної похибки, взятої з протилежним знаком. Вона додається до результату вимірювання, щоб вилучити систематичну похибку.

Систематичні і випадкові похибки. Систематичні похибки можуть бути сталими і змінними. Змінні систематичні похибки поділяють на прогресуючі, періодичні і такі, що змінюються за складним законом.

Прогресуючими називають такі систематичні похибки, які постійно зростають або зменшуються.

Періодичними вважають систематичні похибки, знак і значення яких періодично змінюються.

Систематичні похибки, що змінюються за складним законом, можна виразити графічно або аналітично. Якщо це дуже складно, то їх доцільніше зарахувати до випадкових похибок.

Одним із завдань вимірювального експерименту є виявлення систематичних похибок. Важливість його полягає в тому, що така невиявлена похибка набагато не безпечна, ніж випадкова, бо вона постійно спотворює результат вимірювання.

Кінцевою метою виявлення систематичних похибок є їх вилучення і врахування. Під вилученням систематичних похибок розуміють зменшення їх значень до рівня окремих невеликих складових випадкової похибки. Не вилучені залишки систематичних похибок трактуються як випадкові.

Універсального способу вилучення систематичних похибок немає. Серед відомих способів найпоширенішими є такі:

- вилучення джерел похибок, переважно похибок установлення;

- попереднє визначення похибок і їх урахування шляхом введення поправок, знайдених при перевірці засобів вимірювання, включаючи поправки на додаткові похибки.

До спеціальних способів вилучення систематичних похибок належать: спосіб заміщення, спосіб компенсації похибки за знаком, спосіб протиставлення, спосіб симетричних спостережень.

Спосіб заміщення полягає в тому, що спочатку на вхід вимірювального приладу подають вимірювану величину, а потім замінюють її величиною з таким відомим зна­ченням х_Д, при якому показ приладу залишається попереднім. Отже, невідоме значення вимірюваної величини X знаходять за відомим значенням х_Д , відтвореним мірою при заміщенні.

Спосіб компенсації похибки за знаком полягає в тому, що дану величину вимірюють двічі, але умови вимірювання змінюють так, щоб стала систематична похибка, яка підлягає вилученню (відома за походженням, але невідома за значенням), входила в результати вимірювань з протилежними знаками. Тоді середнє арифметичне результатів стає вільним від цієї похибки.

Спосіб компенсації похибки можна використати для вилучення похибок, джерела яких мають направлену дію. Однак, якщо похибка така, що прогресує, то цей спосіб забезпечує тільки часткове її вилучення.

Спосіб протиставлення полягає в тому, що вимірювана величина двічі порівнюється з величиною, яка відтворюється мірою, причому перед другим порівнянням вони взаємно міняються місцями у вимірювальному колі. Результат вимірювання у вигляді середнього пропорційного між значеннями міри при першому і другому порівняннях зовсім не залежить від коефіцієнта передачі вимірювальної схеми. Тому стала систематична похибка цього коефіцієнта, яка існує при одноразовому вимірюванні, повністю вилучається.

Випадкові похибки. Випадкові похибки виникають внаслідок випадкових та не­передбачених змін властивостей засобів і умов вимірювання та властивостей органів чуття спостерігача. Вони можуть бути зумовлені недосконалістю методу вимірювання, тобто недостатньою обґрунтованістю його теорії або допущеними спрощеннями, внаслідок чого не тільки значення, але й знаки похибок залишаються невідомими, випадковими є невизначені за своєю величиною або недостатньо вивчені похибки, в появі різних значень яких нам не вдається встановити закономірності. Вони визначаються складною сукупністю причин, які трудно проаналізувати, їх значення не можуть бути передбачені, а для всього їх загалу можна встановити закономірність лише для частоти появи їх різних значень. Присутність випадкових похибок (на відміну від систематичних) легко виявляється при повторних вимірюваннях, як деякий роз­кид результатів. Переважно поява випадкових похибок є стаціонарним випадко­вим процесом.

Якщо значення, які може набувати випадкова величина, утворюють дискретний (скінченний або нескінченний) ряд чисел, то така випадкова величина називається дискретною. Якщо ж значення випадкової величини заповнюють цілий проміжок (скінченний або нескінченний), то випадкову величину називають неперервною.

Кожному значенню випадкової величини х_n дискретного типу відповідає певна ймовірність р_п її появи. Кожному проміжку (а, b) із області значень випадкової величини неперервного типу також відповідає певна ймовірність р(а < х < b) того, що значення випадкової величини буде в певному проміжку.

Співвідношення, які встановлюють зв'язок між можливими значеннями ви­падкових величин і їх ймовірностями, називають законом розподілу випадкової вели­чини. Закон розподілу дискретної випадкової величини задається рядом розподілу. Тому різноманітність величин випадкових похибок характеризують вказуванням закону розподілу їх ймовірностей або вказуванням параметрів цього закону, розвинутих в теорії ймовірностей і в теорії інформації.

Випадкові похибки описуються функціями розподілу: інтегральною і диференційною.

Інтегральною функцією розподілу результатів спостережень називають за­лежність ймовірності того, що результат спостережень х_і в і-му досліді виявиться меншим, ніж деяке біжуче значення х від самої величини X:

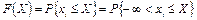
(3.4)

де Р – символ імовірності події, вказаної у фігурних дужках.

Значення інтегральної функції в точці X числове дорівнює імовірності того, що випадкова величина х_і внаслідок і-го спостереження виявиться лівіше від точки X. При переміщенні точки X вздовж осі ОХ ця ймовірність буде, напевно, змінюватись, але зменшитися при переміщенні вправо вона не може. Тому інтегральна функція розподілу є неспадною функцією аргументу. Загалом її значення при переміщенні точки X із "–" в "+" змінюється від 0 до 1. Теоретична інтегральна функція неперервна, тобто результат спостереження може мати яке завгодно наперед вибране значення з нульовою ймовірністю. Практично роздільча властивість вимірювальних засобів ділить всю область значень вимірюваної величини на відрізки, в котрих спостерігач не відрізняє зміни вимірюваної величини. Тому в межах кожного відрізка інтегральна функція розподілу зберігає постійне значення і стрибкоподібно змінюється при переході границі до якогось кінцевого значення. В цифрових вимірювальних системах ці сходинки конкретно відповідають одиницям останнього розряду, а в аналогових – якійсь часточці ціни поділки.

Але переважно згадані вище обставини не забороняють вважати інтегральну функцію розподілу результатів спостережень безперервною функцією і це спрощує аналіз випадкових похибок.

Похибку Δ можна розглядати також як випадкову величину, що набуває в різних дослідах різного значення Δ_і. Початок координат для похибок Δ відповідає значенню Х = х. Інтегральна функція розподілу похибок відповідає інтегральній функції розподілу результатів спостережень х_і

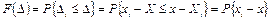
(3.5)

У метрології при розгляданні випадкових похибок вимірювання частіше засто­совують диференціальну функцію розподілу, котра є функцією, похідною від інтегральної за своїм аргументом

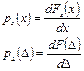
(3.6)

Диференціальну функцію розподілу р_х(х) часто називають щільністю ймовір­ностей, а її графічну форму – кривою розподілу. Найчастіше ця крива має форму дзвона (рис. 2).

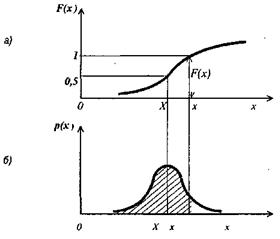
Рис. 2. Функції розподілу: а – інтегральна; б – диференціальна

Інтегруванням диференційної функції розподілу легко отримати інтегральну функцію

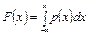
(3.7)

Для щільності ймовірностей мають виконуватись такі умови:

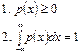
Другу умову називають умовою нормування щільності ймовірностей. Це значить, що площа під кривою розподілу в межах -∞ ... +∞ дорівнює одиниці, або інакше кажучи – ймовірність появи результату спостереження у вказаному інтервалі є вірогідною подією. Розмірність щільності ймовірності випадкової величини х виражається як х^-1. Добуток р(х)dх називається елементом ймовірності і він дорівнює ймовірності того, що випадкова величина х буде мати значення в інтервалі dх. Якщо крива розподілу р(х) відома, то можна визначити ймовірність попадання результату спостереження в будь-який заданий інтервал х₁, х₂

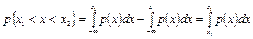
(3.8)

Знаючи інтегральну функцію розподілу, ймовірність попадання результату спостереження х у вказаний інтервал визначають за різницею значень функції розподілу на межах цього інтервалу

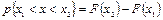
(3.9)

Ймовірність попадання результатів спостережень в заданий інтервал х₂ – х₁ можна визначати графічним способом за інтегральною функцією розподілу (рис. 3, а) і за кривою розподілу щільності ймовірності (рис. 3, б).

У першому випадку шукана ймовірність визначається різницею значень ординат, що відповідають аргументам х₁ і х₂, а в другому випадку – площею під кривою розподілу, що обмежена вздовж осі х значеннями х₁ та х₂. Отже, за кривою розподілу можна довідатись, які інтервали значень випадкових похибок більш ймовірні, а які менш ймовірні. За кривою розподілу випадкових розмірів х (рис. 3, б) можна твердити, що ймовірності зростають при наближенні до деякої частини кривої, котра виглядає як середня, а потім зменшуються, прямуючи до нуля. При повторних вимірюваннях одної і тої ж фізичної величини X максимальна ймовірність припадає на значення, близькі до істинного X. Для значень х, що дуже відрізняються від X, ймовірність зменшується при збільшенні цієї різниці х-Х, тобто більшим похибкам відповідає менша ймовірність їх появи. Якщо припустити, що причини, які спричиняють похибки вимірювання, проявляють себе випадково, то нема підстав твердити що якісь похибки (додатні або від'ємні) мають більшу імовірність. Тому можливим є прийняти за оцінку істинного значення вимірюваної величини таке значення, що відповідає центру ваги площі фігури, обмеженої кривою розподілу та віссю абсцис. Координата, що відповідає центру ваги, називається математичним сподіванням.

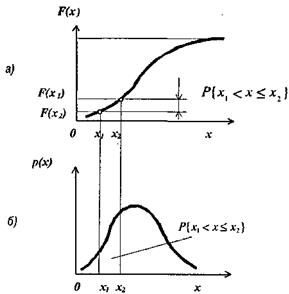
Рис. 3. Ймовірність попадання результатів спостережень

в заданий інтервал

Математичне сподівання визначається як початковий момент першого порядку кривої розподілу

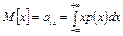
(3.10)

Отже, математичне сподівання випадкової величини х є деяким постійним чис­лом, що є параметром розподілу. Числове значення вимірюваної величини, що від­повідає математичному сподіванню, приймають за оцінку істинного значення X, тобто

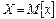
(3.11)

Але при визначенні емпіричної кривої розподілу математичне сподівання переважно не збігається з істинним значенням вимірюваної величини.

Розподіл випадкової величини для загального випадку показаний на рис. 4.

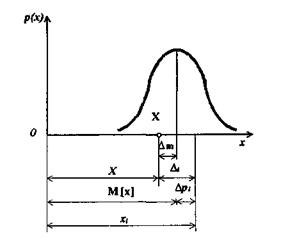
Рис. 4. Характеристики випадкової похибки

З рис. 4 видно, що оцінка істинного значення м[х] відрізняється від істинного значення X на деяку Δ_т, котра є математичним сподіванням похибки вимірювання. Знайдемо математичне сподівання похибки вимірювання

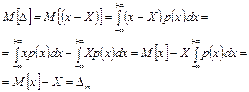
(3.12)

Математичне сподівання похибки вимірювання становить деяку середню постійну похибку, котра повторюється в кожному і-му спостереженні. Цю похибку позначимо Δ_т, і назвемо систематичною похибкою. Дослідження процесів вимірювання показує, що систематична похибка інколи не залишається постійною, а змінюється плавно за якимось законом. Виникнення систематичної похибки є наслідком дії одної або декількох причин, що мають постійний або дещо змінний характер. Наприклад, неправильне настроювання нуля вимірювального приладу призводить до систематичної похибки, яка буде присутня в результаті кожного окремого спостереження.

Строгіше систематична похибка визначається як відхилення математичного сподівання результатів спостережень від істинного значення вимірюваної величини

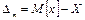
(3.13)

а випадкова похибка – як різниця між результатом одноразового спостереження і математичним сподіванням результатів

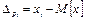
(3.14)

Отже, кожну похибку одноразового спостереження можна представити сумою систематичної та випадкової похибок

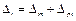
(3.15)

Такий стан проілюстровано на рис. 4.

При застосуванні цих умовних позначень істинне значення вимірюваної величини визначається так:

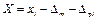
(3.16)

Якщо врахувати, що систематична похибка є постійною для деякої сукупності результатів вимірювання, а випадкова змінюється і за значенням і за знаком для кожного одноразового спостереження, то істинне значення визначається так:

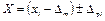
(3.17)

Значення х_і – Δ_т називається виправленим результатом, якщо Δ_т вдається визначити, аналізуючи експеримент. Випадкова похибка Δ_рі залишається невідомою і вимагає чіткішого обмеження, (з врахуванням ймовірно-статистичних законів розпо­ділу). Взагалі, при одноразовому спостереженні невідомими є обидві складові похибки вимірювання, і тому результат можна подати тільки в такому вигляді:

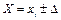
(3.18)

де Δ – межа похибки вимірювання (максимальне значення суми Δ_т і Δ_р за модулем).