ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ СОЕДИНЕНИЙ ЗВЕНЬЕВ
Последовательное соединение звеньев. Последовательным называется такое соединение звеньев, при котором выход каждого предыдущего связан со входом последующего звена (рис. 73). В образованной разомкнутой цепи воздействия передаются последовательно от одного звена к другому.
При последовательном соединении n звеньев с передаточными функциями W1 (p), W2 (p), ..., Wn (p) уравнения связи в операторной форме имеют вид
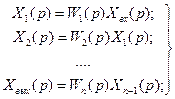
Исключив из данных уравнений все промежуточные переменные, кроме входной и выходной величин, получим
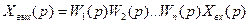

Рис. 73. Схема последовательного соединения звеньев.
Из этой зависимости определяем, что цепочку из последовательно соединенных звеньев можно заменить одним сложным звеном с передаточной функцией
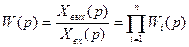 (70)
(70)
Следовательно, получаем правило 1:
передаточная функция системы последовательно соединенных звеньев равна произведению передаточных функций всех звеньев, входящих в соединение.
Коэффициент передачи k цепи последовательно соединенных звеньев равен также произведению коэффициентов передачи всех звеньев:
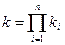 (71)
(71)
Произведя в выражении (70) замену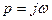 , получим комплексную передаточную функцию, или амплитудно-фазовую частотную характеристику (АФЧХ),
, получим комплексную передаточную функцию, или амплитудно-фазовую частотную характеристику (АФЧХ),
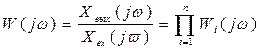 (72)
(72)
Таким образом, комплексная передаточная функция последовательно соединенных звеньев равна произведению комплексных передаточных функций всех звеньев, входящих в соединение.
Представляя АФЧХ i-гo звена в виде
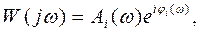 (73)
(73)
где 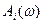 и
и 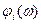 —соответственно амплитудная и фазовая частотные характеристики 1-го звена, из формулы (72) получаем
—соответственно амплитудная и фазовая частотные характеристики 1-го звена, из формулы (72) получаем
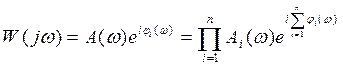 (74)
(74)
На основании данной формулы записываем выражения для амплитудной и фазовой частотных характеристик последовательного соединения звеньев:
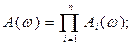 (75)
(75)
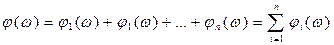 (76)
(76)
При последовательном соединении устойчивых звеньев полученная система будет минимально-фазовой, т. е. ее передаточная функция в правой полуплоскости р не будет иметь ни нулей, ни полюсов. Если хотя бы одно из последовательно соединенных звеньев неустойчиво, то и вся разомкнутая система будет неустойчивой (неминимально-фазовой).
Рассмотрим пример последовательного соединения звеньев.
Пример 1. Пусть требуется исследовать динамические свойства схемы (рис 74 а), состоящей из последова- тельно соединенных RC-цепи и операционного усилителя в режиме интегратора. Параметры схемы известны: 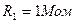 ;
; 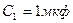 ;
; 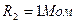 ;
; 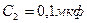 .
.
Так как входное сопротивление усилителя велико, то RС-цепь практически можно считать ненагруженной. В случае необходимости нагрузку можно учесть. По своим динамическим свойствам рассматриваемая цепь эквивалентна апериодическому звену с передаточной функцией
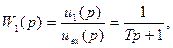
где 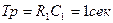 .
.
Операционный усилитель в режиме интегратора имеет передаточную функцию
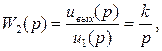
где
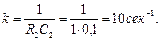 |
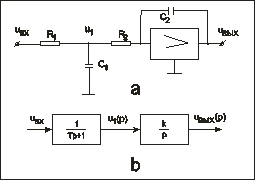
Рис. 74. Принципиальная (а) и структурная (б) схемы RC-цепи и операционного
усилителя.
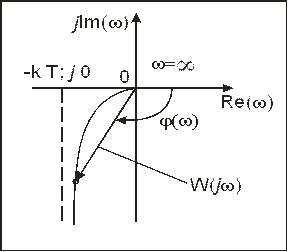
Рис. 75. Амплитудно-фазовая характеристика
последовательно соединенных звеньев.
В соответствии с принципиальной схемой (рис. 74, а) и полученными выше передаточными функциями звеньев на рис. 74, б изображена структурная схема исследуемого устройства.
Передаточная функция двух последовательно соединенных звеньев
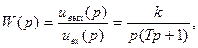
а комплексная передаточная функция системы
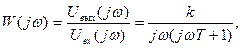 (77)
(77)
Построим годограф, описываемый концом вектора  при
при 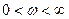 , путем выделения действительной и мнимой частей в выражении (77):
, путем выделения действительной и мнимой частей в выражении (77):
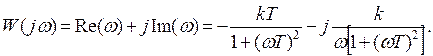 Вертикальная прямая, проходящая через точку (—kT; j0), является асимптотой для рассматриваемого годографа при убывании со к нулю (рис. 75).
Вертикальная прямая, проходящая через точку (—kT; j0), является асимптотой для рассматриваемого годографа при убывании со к нулю (рис. 75).
Параллельное соединение звеньев. Параллельным (согласным) называется
такое соединение звеньев, при котором входные воздействия всех звеньев одинаковы,
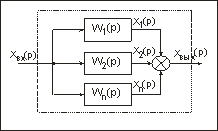
Рис. 76. Схема параллельного соединения
звеньев.
а их реакции алгебраически, суммируются (рис. 76).
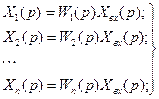 По определению, для каждого звена получим:
По определению, для каждого звена получим:
Реакция системы равна сумме реакций всех звеньев:
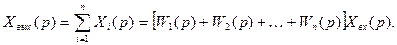

Поэтому группу параллельно соединенных звеньев можно заменить одним эквивалентным звеном (системой), передаточная функция которого равна сумме передаточных функций всех звеньев:
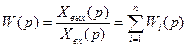
(78)
Следовательно, получаем правило 2:
передаточная функция параллельно (согласно) соединенных звеньев равна сумме передаточных функций всех звеньев, входящих в соединение.
В частном случае, при параллельном соединении только усилительных звеньев коэффициент передачи равен сумме коэффициентов передачи отдельных звеньев:
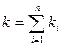
(79)
При параллельном соединении дифференцирующего и усилительного звеньев (рис. 77, а) передаточная функция
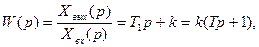
где 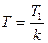 - постоянная времени форсирующего звена.
- постоянная времени форсирующего звена.
Очевидно, этому соединению соответствует эквивалентная схема последовательного соединения усилительного и форсирующего звеньев (рис. 77, б).
Параллельное соединение интегрирующего и усилительного звеньев
(рис. 78, а) описывается передаточной функцией
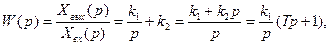
где  - постоянная времени форсирующего звена.
- постоянная времени форсирующего звена.
Полученная формула показывает, что схеме (рис. 78) соответствует эквивалентная схема последовательного соединения интегрирующего и форсирующего звеньев (рис. 78, б).
Из рассмотренных примеров видно, что параллельное соединение позволяет получить различные законы управления в автоматических системах: введение интеграла, форсировки и т. п. Построение частотных характеристик данного типа соединения звеньев связано с некоторыми трудностями. Комплексная
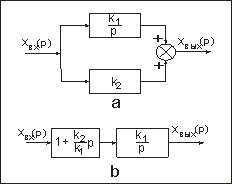
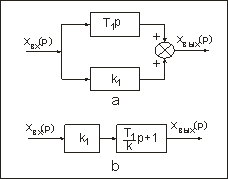
Рис. 77. Структурная {а) я эквивалентная (б) схемы параллельного соединения дифференцирующего и усилительного звеньев.
Рис. 78. Структурная (а) и эквивалентная (6) схемы параллельного соединения интегрирующего и усилительного звеньев.
передаточная функция определяется аналогично формуле (78) как сумма
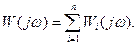
При построении годографа АФЧХ по этой формуле каждая точка получается геометрическим суммированием векторов 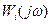 на одинаковых частотах.
на одинаковых частотах.
Обратная связь. Понятие обратная связь имеет фундаментальное значение в теории управления. Любая автоматическая система, построенная в соответствии с принципом управления по отклонению, имеет основную отрицательную обратную связь. Кроме основной обратной связи, системы могут иметь дополнительные, предназначенные для коррекции динамических свойств отдельных звеньев и системы в целом. Дополнительные связи могут быть отрицательными или положительными в зависимости от их назначения.
Обратной связью называется цепь передачи воздействий с выхода системы (звена) на ее вход.
Как видно из рис. 79, при наличии обратной связи образуется замкнутый контур передачи воздействий от одного звена к другому. Выходной сигнал первого звена (реакция системы в целом) подается на вход второго, а выходной сигнал второго звена Хо.с. с соответствующим знаком («—» или «+») суммируется со входным сигналом системы Хвх. В результате на вход первого звена, стоящего
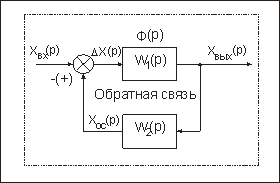 в прямой цепи системы, подается сигнал
в прямой цепи системы, подается сигнал
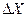 , равный алгебраической сумме:
, равный алгебраической сумме:
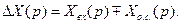 (80)
(80)
Данное выражение называют уравнением замыкания системы (контура). Оно записано в операторном виде и является основным признаком наличия обратной связи в системе. Если в правой части уравнения (80) будет знак «—» то обратная связь называется отрицательной и соответствует
Рис- 79, структурная схема системы с обратной связью, состоящей из двух звеньев с передаточными функциями 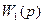 и
и 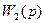
принципу управления по отклонению, если знак «+», то имеем положительную обратную связь.
Кроме уравнения замыкания, система с обратной связью описывается уравнением прямой цепи
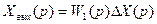 (81)
(81)
и уравнением цепи обратной связи
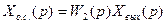 (82)
(82)
Рассматривая совместно уравнения (80) — (82), получаем
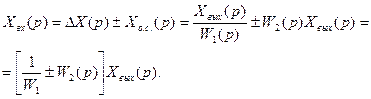 (83)
(83)
Согласно общему определению искомая передаточная функция системы с обратной связью Ф (р) равна отношению изображения выходного сигнала к изображению входного сигнала по Лапласу при нулевых начальных условиях:

(84)
где знак «+» — для отрицательной обратной связи; знак «—» - для положительной обратной связи.
Таким образом, получаем правило 3:
передаточная функция звена (системы), охваченного обратной связью, равна частному, в числителе которого стоит передаточная функция охватываемого звена, а в знаменателе — сумма (разность) единицы и произведения передаточной функции охватываемого звена на передаточную функцию звена обратной связи.
В теории управления чаще встречаются отрицательные обратные связи, поэтому пользуются передаточной функцией
 (85)
(85)
Так как передаточные функции звеньев, включенных в замкнутый контур, обычно являются дробно-рациональными функциями
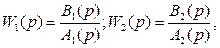
то уравнение (85) запишем в виде
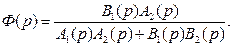 (86)
(86)
Из рассмотрения уравнений (84) и (86) видно, что обратные связи открывают большие возможности для синтеза автоматических систем с требуемыми динамическими свойствами. Так, например, из уравнения (86) вытекает, что нули Ф (р) совпадают с нулями W1 (p) и полюсами W2 (р). Однако полюсы передаточной функции замкнутой системы отличаются от полюсов функций W1 (p) и W2 (р).Это приводит к тому, что устойчивые звенья, включенные в замкнутый контур, могут образовать неустойчивую систему. И наоборот, замкнутый контур, составленный из звеньев, среди которых имеются неустойчивые, может оказаться устойчивым.
Общее выражение для комплексной передаточной функции системы с обратной связью (контура), определяемое при гармонических сигналах, в соот-

| 
|
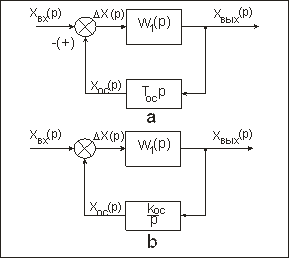
Рис 80. Структурные схемы системы с ЖОС Рис. 81. Структурные схемы систем с ГОС(о)
(а) и ЕООС (б). и ИООС (б).
ветствии с формулой (85) можно записать так:
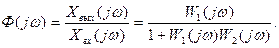 (87)
(87)
По этой формуле производится расчет частотных характеристик систем с обратными связями.
Кроме разделения обратных связей на отрицательные и положительные, их можно классифицировать по другим признакам. В частности, по виду передаточной функции W2(p) звена обратной связи (рис. 79) различают жесткую обратную связь (ЖОС), гибкую обратную связь (ГОС) и интегрирующую обратную связь (ИОС).
Если в цепь обратной связи включено усилительное звено с передаточной функцией kоc., то такая связь называется жесткой обратной связью (рис. 80, а). В соответствии с выражением (84) передаточная функция такой системы (контура)
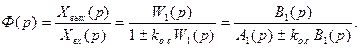
В весьма распространенном в следящих системах случае применяется единичная отрицательная обратная связь (ЕООС) (рис. 80, б), при которой
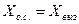 ,так как kоc = 1 и W1 (р). = W (р). Передаточная функция замкнутой следящей системы
,так как kоc = 1 и W1 (р). = W (р). Передаточная функция замкнутой следящей системы
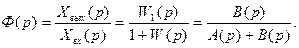 (88)
(88)
в режиме вынужденных установившихся гармонических колебаний частотные свойства замкнутой системы с ЕООС определяются комплексной передаточной Функцией
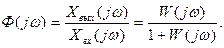 (89)
(89)
Если в цепь обратной связи включено дифференцирующее звено с переданной функцией W2 (р) = Тоср, то такая связь называется гибкой (дифференцирующей) обратной связью (рис. 81, а). При этом сигнал обратной связи

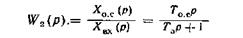
|
пропорционален производной от выходного сигнала. Такую связь обычно применяют для того, чтобы замкнутый контур обладал свойствами интегратора, а также с целью стабилизации систем. Особенность гибких обратных связей заключается в том, что воздействия передаются через них на вход системы только при изменении сигнала Xвых (t) во времени.
 Включение в цепь обратной связи реального дифференцирующего звена с передаточной функцией Включение в цепь обратной связи реального дифференцирующего звена с передаточной функцией
|
| Рис. 82. Принципиальная (а) и структурная (б) схемы электронного усилителя с обратной связью. |
также приводит к гибкой обратной связи. Однако она будет инерционной в связи с наличием апериодического звена с постоянной времени Та. Такая связь получила название изодромной* обратной связи. Впервые изодромные обратные связи применялись для стабилизации скорости вращения паровых машин. Так как такие регуляторы обеспечивали постоянную скорость вращения независимо от нагрузки, то их и стали называть равнобегущими.
Обратная связь называется интегрирующей, если в ее цепь включен интегратор. Как и рассмотренные выше связи, она может быть отрицательной или положительной. На рис. 81, б изображена структурная схема системы с интегрирующей отрицательной связью (ИООС). Обычно такая связь применяется при необходимости дифференцирования задающего воздействия. Передаточные функции системы с дифференцирующими и интегрирующими обратными связями легко получить по формуле (84) при соответствующих значениях операторов W2 (p).
Итак, приведенные правила 1, 2 и 3 в сочетании с подбором передаточных функций звеньев позволяют получить любую структуру. В частности, с их помощью можно получить многие звенья, пользуясь всего лишь несколькими элементарными. Покажем это на примерах.
Пример 2.Усилительное звено охвачено жесткой отрицательной обратной связью (рис. 82).
В разомкнутом состоянии усилитель имеет коэффициент усиления  .
.
 На вход первого каскада усилителя поступает напряжение Напряжение обратной связи иол снимается с потенциометра па выходе усилителя:
На вход первого каскада усилителя поступает напряжение Напряжение обратной связи иол снимается с потенциометра па выходе усилителя:
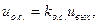
где 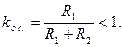
Коэффициент усиления k усилителя, охваченного обратной связью,можно определить по формуле (84), которая в рассматриваемом случае принимаетвид

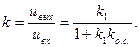
* Слово изодром греческого происхождения и означает равнобегусций.
 При При 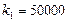 и и 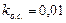 получим получим
|
На первый взгляд может показаться, что обратная связь ничего не дает, кроме резкого уменьшения коэффициента усиления. Однако это не так.
| Рис. 83. Структурные схемы интегратора с жесткой (а) и гибкой (б) отрицательными обрати ими связями. |
Действительно, у реальных усилителей коэффициент &х не является постоянным и может изменяться в широких пределах. Предположим, что это изменение составляет ± 20% от номинального значения. Это значит, что k1 может изменяться от 40 000 до 60 000. Определим соответствующие минимальное kmin и максимальное kmax значения коэффициента усиления усилителя с обратной связью:

Как видно из этих выражений, значение коэффициента k практически не изменяется.
Таким образом, при koc = const, что достигается применением высококачественного
потенциометра, отрицательная обратная связь обеспечивает стабилизацию коэффициента усиления усилителя.
Пример 3. Интегрирующее звено охвачено жесткой отрицательной обратной связью (рис. 83, а). Передаточная функция такой системы

Дата добавления: 2015-07-14; просмотров: 7719;
