Характеристики типовых звеньев автоматических систем
| Передаточная функция | ||
Пропорциональное
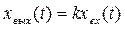
| 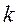
| 
|
Апериодическое
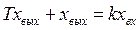
| 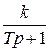
| 
|
Колебательное
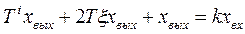
| 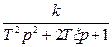
| 
|
Интегрирующее
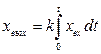
| 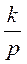
| 
|
Дифференцирующее
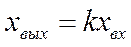
| 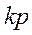
| 
|
Запаздывающее
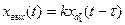
| 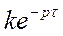
| 
|
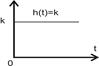
Таким образом, пропорциональное звено мгновенно копирует входной сигнал, изменяя его масштаб в k раз. Переходной процесс отсутствует. Следовательно, пропорциональное звено является безинерционным.
Выясгим частотные свойства пропорционального звена. Из уравнения (48) следует, что при входном сигнале xвх = Авк sin ωt выходной сигнал
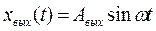
где Aвых — амплитуда выходного сигнала.
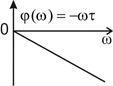
Таким образом, в пропорциональном звене выходной и входной сигналы находятся в фазе. Кроме того, амплитуда выходного сигнала в k раз отличается от амплитуды входного. Следовательно, фазовая частотная характеристика
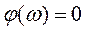 (51)
(51)
| Частотные характеристики | ||
| амплитудная | фазовая | логарифмические |
| 
| 
|
| 
| 
|
| 
| 
|
| 
| 
|

| 
| 
|

| 
| 
|
и амплитудная частотная характеристика
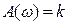 (52)
(52)
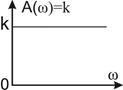
Подчеркнем, что частотные характеристики пропорционального звена не зависят от частоты.
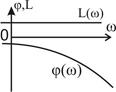
В инженерной практике широко применяются логарифмические частотные характеристики (ЛЧХ). Какой они имеют вид для пропорционального звена и как их построить? Фазовая характеристика φ(ω), как обычная, так и логарифмическая, равна нулю. А вот логарифмическая амплитудная частотная характеристика (ЛАЧХ) L (ω) имеет особенности. Ее уравнение
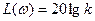 (53)
(53)
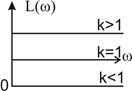
Следовательно, ЛАЧХ является прямой, проведенной на уровне 20 lg k. При усилении сигнала (к > 1) ЛАЧХ расположена выше оси частот, а при ослаблении (к < 1) — ниже оси частот. Если k = 1, то L (ω) = 0, т. е. ЛАЧХ проходит по оси частот.
Апериодическое звено. Звено называется апериодическим, если его дифференциальное уравнение имеет вид
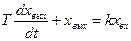 (54)
(54)
где Т — постоянная времени; k — коэффициент передачи.
Передаточная функция
 (55)
(55)
Примерами апериодического звена являются рассмотренные во второй беседе магнитный и электромашинные усилители, электрические двигатели и т. д.
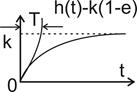
Переходная функция апериодического звена достигает своего установившегося значения k не сразу, а постепенно по экспоненциальному (апериодическому) закону, из-за чего звено и получило свое наименование. Тем самым апериодическое звено отражает инерционность изучаемого процесса, и поэтому его иногда называют инерционным звеном. Однако мы откажемся от этого наименования, так как и некоторые другие звенья, содержащие множитель Тр  1 в знаменателе передаточной функции, являются инерционными. Апериодичность же переходного процесса присуща только этому типовому звену, причем мерой инерционности является постоянная времени Т: переходной процесс заканчивается при t = (3
1 в знаменателе передаточной функции, являются инерционными. Апериодичность же переходного процесса присуща только этому типовому звену, причем мерой инерционности является постоянная времени Т: переходной процесс заканчивается при t = (3  4) T. Чем меньше Т, тем апериодическое звено ближе по своим динамическим свойствам к пропорциональному. Например, постоянная времени электронных усилителей АС равна 10 -4— 10 -6 сек. Поэтому эти усилители рассматривают как пропорциональные звенья.
4) T. Чем меньше Т, тем апериодическое звено ближе по своим динамическим свойствам к пропорциональному. Например, постоянная времени электронных усилителей АС равна 10 -4— 10 -6 сек. Поэтому эти усилители рассматривают как пропорциональные звенья.
Элемент АС может быть отображен апериодическим звеном, если он содержит хотя бы одну емкость энергии. Такими емкостями в электрических цепях являются конденсатор С и индуктивность L: в конденсаторе накапливается энергия электрического поля, а в индуктивности - магнитного. Емкостями энергии в механических системах являются движущиеся массы, пружины и т. д. Накопление и рассеивание энергии в апериодическом звене происходит не мгновенно, а постепенно, что и является причиной инерционности физических явлений.
Частотные характеристики апериодического звена можно получить из уравнения (54), найдя его частное решение. Однако эти характеристики легче найти следующим образом.
Вначале найдем амплитудно-фазовую характеристику
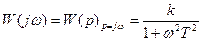 (56)
(56)
Выделим из выражения (56) действительную и мнимую части и тем самым найдем вещественную
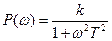 (57)
(57)
и мнимую
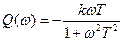 (58)
(58)
частотные характеристики.
Теперь определим амплитудную
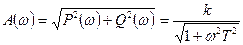 (59)
(59)
и фазовую
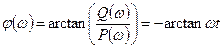 (60)
(60)
частотные характеристики, которыми наглядно отображаются частотные свойства звена.
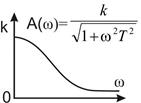
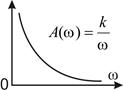
Из анализа амплитудной частотной характеристики А (ω) следует, что апериодическое звено обладает свойством фильтра: хорошо пропускает сигналы малых частот и плохо — больших, поскольку А (ω) с ростом частоты убывает, и следовательно, убывает амплитуда выходного сигнала.
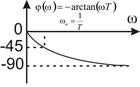
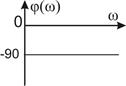
Из анализа фазовой частотной характеристики φ(ω) следует, что выходные колебания отстают по фазе от входных. Это отставание изменяется в пределах от 0° до -90°. На частоте 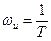
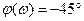 . Как будет показано в дальнейших беседах, вносимый апериодическим звеном отрицательный сдвиг фаз неблагоприятно сказывается на устойчивости АС.
. Как будет показано в дальнейших беседах, вносимый апериодическим звеном отрицательный сдвиг фаз неблагоприятно сказывается на устойчивости АС.
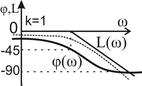
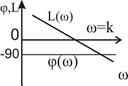
Точная ЛАЧХ апериодического звена L(ω) представляет собой кривую (пунктирная линия в табл. 1). Однако в инженерной практике точную ЛАЧХ заменяют ломаной, образованной двумя асимптотами, которые сопрягаются на частоте излома 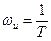 . В области больших частот (ω> ωи) асимптота имеет наклон — 20 дб/дек. Максимальная ошибка (З дб) при замене точной ЛАЧХ асимптотической будет на частоте излома ω.
. В области больших частот (ω> ωи) асимптота имеет наклон — 20 дб/дек. Максимальная ошибка (З дб) при замене точной ЛАЧХ асимптотической будет на частоте излома ω.
По сравнению с обычными, логарифмические частотные характеристики апериодического звена имеют ряд существенных достоинств. В самом деле, при изменении параметров звена k и Т обычные характеристики деформируются, а логарифмические — нет, они только перемещаются вдоль осей координат. Это обстоятельство позволяет при построении ЛЧХ применять шаблоны. Кроме того, асимптотическая ЛАЧХ представляет собой ломаную, которую весьма просто построить.
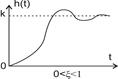
Колебательное звено. Элемент автоматической системы может быть отражен колебательным звеном, если он содержит как минимум две емкости различных видов энергии; в одной емкости накапливается потенциальная, а в другой — кинетическая энергия. Канал, по которому емкости обмениваются энергией, обладает сопротивлением. На нем происходят безвозвратные для элемента потери энергии. Мерой этих потерь является коэффициент затухания ξ: чем больше ξ, тем больше потери энергии. При 0 < ξ < 1 переходный процесс колебательный, причем чем меньше ξ, тем колебания более интенсивны. В идеальном случае ξ =0, Это значит, что потери энергии отсутствуют, и элемент сохраняет неизменным первоначальный запас энергии, ввиду чего звено называется консервативным. Тогда переходный процесс будет незатухающим. Если ξ ≥ 1, то потери энергии настолько велики, что переходный процесс перестает быть колебательным. В этом случае звено иногда называют апериодическим второго порядка, и его можно заменить двумя последовательно соединенными апериодическими звеньями.
Примерами колебательного звена являются рассмотренные ранее электрическая цепь и механическая система (рис. 65). В электрической цепи емкость С накапливает энергию электрического поля (потенциальная энергия), а индуктивность L — энергию электромагнитного поля (кинетическая энергия). Безвозвратные потери происходят на сопротивлении R. Если сопротивление R невелико, то контур будет колебательным. В механической системе движущая
масса накапливает кинетическую, а пружина — потенциальную энергию. Потери энергии происходят в демпфере.
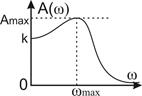
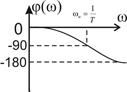
Амплитудная частотная характеристика колебательного звена А (ω) имеет максимум Аmax на резонансной частоте ωmax.Чем меньше ξ, тем больше Аmax. Колебательное звено создает отрицательный сдвиг фаз, который изменяется от 0° при ω = 0 до —180° при ω = ∞. На частоте 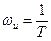
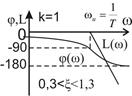
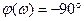 . Логарифмическую амплитудную частотную характеристику L (о) при 0,35 < ξ < 1,3 обычно заменяют асимптотической, которая в области больших частот (ω > ωи) имеет наклон — 40 дб/дек. Частотные характеристики колебательного звена также, как и переходная функция, зависят от коэффициента затухания ξ.
. Логарифмическую амплитудную частотную характеристику L (о) при 0,35 < ξ < 1,3 обычно заменяют асимптотической, которая в области больших частот (ω > ωи) имеет наклон — 40 дб/дек. Частотные характеристики колебательного звена также, как и переходная функция, зависят от коэффициента затухания ξ.
Интегрирующее звено. Интегрирующим называется такое звено, выходная величина которого пропорциональна интегралу по времени от входной величины:
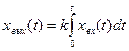 (61)
(61)
Продифференцируем левую и правую части этого уравнения:
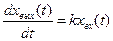 (62)
(62)
Из формулы (62) видно, что скорость изменения выходной величины интегрирующего звена пропорциональна входной величине. При этом коэффициент передачи k численно равен скорости изменения выходной величины при единичном значении входной величины. Поэтому его называют коэффициентом передачи по скорости. Если входная и выходная величины имеют одинаковые размерности, например являются напряжением, то размерность k равна ceк-1. В этом случае удобно применять не коэффициент передачи, а постоянную времени интегрирующего звена
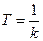
Тогда уравнение звена примет вид
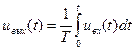 (63)
(63)
или
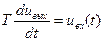 (64)
(64)
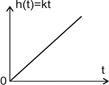
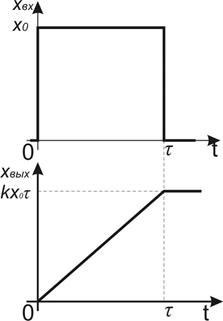
При постоянном (ступенчатом) входном сигнале выходной сигнал интегрирующего звена изменяется с постоянной скоростью, поэтому его переходная функция непрерывно возрастает по линейному закону.
Отличительным свойством интегрирующего звена является то, что после прекращения действия входного сигнала выходной сигнал звена остается на том уровне, на котором он был в момент исчезновения входного сигнала. Иначе говоря, интегрирующее звено обладает свойством «запоминать», т. е. удерживать последнее значение выходной величины (рис. 67). Благодаря «памяти» интегрирующего звена достигается астатизм автоматической системы.
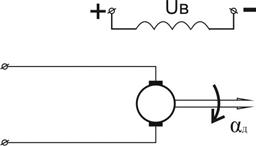
Примером интегрирующего звена является безынерционный электродвигатель, который как интегрирующее звено обладает бесконечной «памятью» (рис. 68). Действительно, если прекратить подачу входного напряжения, то вал двигателя остановится и будет сохранять то угловое положение, которое было достигнуто к моменту исчезновения входного напряжения.
|
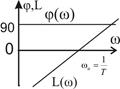
Амплитудная частотная характеристика интегрирующего звена с ростом частоты ω убывает. Следовательно, уменьшается и амплитуда выходной величины. Звено вносит отрицательный сдвиг фаз, который не зависит от частоты вынужденных колебаний и равен —90°. Логарифмическая амплитудная частотная характеристика, которая представляет собой прямую с наклоном — 20 дб/дек, пересекает ось абсцисс в точке ω =k и при частоте ω = 1 сек-1 имеет ординату 20 lg k.
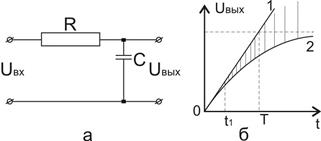
Апериодическое звено как интегратор. При определенных условиях апериодическое звено может быть интегратором. Действительно, рассмотрим электрическую цепь RC, которая является апериодическим звеном (рис. 69,a). Ее дифференциальное уравнение и передаточная функция соответственно имеют вид:
| Рис. 67. К реакции интегрирующего звена на прямоугольный импульс- |
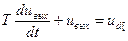 (65)
(65)
|
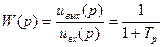 (66)
(66)
где Т = RC — постоянная времени.
| Рис. 68. Принципиальная схема безынерционного электродвигателя. |
Переходную функцию 2 цепи RC на интервале 0 < t < t1 приближенно можно заменить касательной к экспоненте (рис. 69, б). Это значит, что цепь RC является интегрирующим звеном. Максимальное время интегрирования t1 должно быть значительно меньше постоянной времени Т. Чем больше постоянная времени, тем большим можно допустить интервал интегрирования без существенных погрешностей.
|
Рассмотренная цепь RC широко применяется в технике для интегрирования кратковременных импульсов. Ее недостаток — небольшая величина выходного напряжения. Поэтому выходное напряжение цепи необходимо Усиливать.
| Рис. 69. Схема интегрирующей цени RC (а) и ее переходная функция (б). |
Дифференцирующее звено. В соответствии с наименованием звена его выходная величина пропорциональна производной по времени от входной:
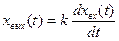 (67)
(67)
Другими словами, выходная величина дифференцирующего звена пропорциональна скорости изменения входной величины.
Если входная и выходная величины звена имеют одинаковую размерность, например являются напряжением, то размерность k равна сек. Тогда уравнение звена удобно записывать в виде
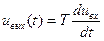 (68)
(68)
где Т — постоянная времени дифференцирующего звена.
Примером дифференцирующего звена является тахогенератор, так как вырабатываемое им напряжение пропорционально скорости вращения его якоря, которая является производной по времени от угла поворота.
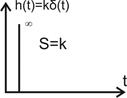
Дифференцирующее звено не пропускает постоянного по величине сигнала. Однако при подаче на его вход ступенчатого сигнала на выходе будет импульс типа дельта-функции.
Возрастающий характер амплитудной частотной характеристики дифференцирующего звена указывает на то, что с увеличением частоты вынужденных колебаний увеличивается и амплитуда выходного сигнала. Таким образом, дифференцирующее звено хорошо пропускает сигналы больших частот и плохо малых. В связи с этим дифференцирующее звено чувствительно к помехам, которые обычно являются высокочастотными. Звено вносит опережение по фазе, равное + 90° и не зависящее от частоты- Логарифмическая амплитудная частотная характеристика дифференцирующего звена представляет собой прямую с наклоном + 20 дб/дек, которая пересекает ось абсцисс при. 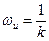 На частоте ω = 1 сек-1 L (ω) = 20 lg k.
На частоте ω = 1 сек-1 L (ω) = 20 lg k.
К типовым звеньям иногда относят и так называемые форсирующие звенья. Различают форсирующие звенья первого и второго порядка. Форсирующие звенья можно сформировать из дифференцирующих и усилительных. Например, форсирующее звено первого порядка имеет дифференциальное уравнение
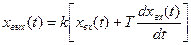
Это звено можно получить путем параллельного соединения дифференцирующего и усилительного звеньев.
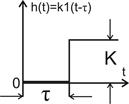
Запаздывающее звено. Звено, которое передает сигнал без искажений, но при этом выходной сигнал по отношению ко входному запаздывает на постоянную величину τ, называется запаздывающим. Такими свойствами обладают длинные электрические линии и трубопроводы. Релейный усилитель также является запаздывающим звеном, причем запаздывание определяется временем срабатывания реле.
Переходная функция запаздывающего звена подобна переходной функции усилительного, но смещена по времени на τ. По частотным свойствам запаздывающее звено также близко к усилительному. Амплитудные характеристики этих звеньев одинаковы, а фазовые — различны.
Запаздывающее звено создает отрицательный сдвиг фаз, который линейно зависит от частоты вынужденных колебаний.
Дата добавления: 2015-07-14; просмотров: 3290;
