СТРУКТУРНАЯ СХЕМА АВТОМАТИЧЕСКОЙ СИСТЕМЫ

Каждая автоматическая система состоит из ряда элементов или функцио­нальных блоков, которые определенным образом взаимодействуют между собой. Динамические свойства элементов системы, как уже известно, можно описать передаточными функциями типовых звеньев направленного действия.

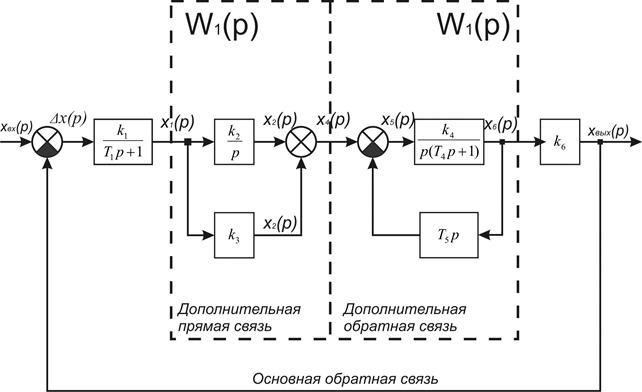
Рис. 72. Структурная схема автоматической системы.

Изучение динамики системы обычно начинают с составления ее структурной схемы. Графическое изображение, показывающее, из каких динамических звеньев состоит система и как они соединены между собой, называется структурной схемой данной системы.

Структурная схема, в отличие от функциональной и принципиальной схем, отображает динамические свойства системы и, по существу, является, графическим условным изображением системы дифференциальных уравнений линейной стационарной системы, отражающих динамику и записанных в операторной форме по Лапласу при нулевых начальных условиях. Структурную схему можно получить из функциональной схемы, если известны передаточные функции и параметры отдельных элементов, образующих систему.

На примере обобщенной структурной схемы автоматической системы с одной регулируемой величиной (рис. 72) определим основные элементы структурной схемы:

1. динамические звенья направленного действия с известными передаточными функциями; они изображаются прямоугольниками, внутри которых записываются операторы преобразования сигналов;

2. связи (соединения звеньев) обозначаются линиями со стрелками, указывающими направление передачи воздействий; различают прямые и обратные связи;

3. сумматоры, в которых складываются или вычитаются воздействия (если воздействия вычитаются, то сектор внутри кружка зачернен);

4. узлы разветвления, в которых воздействие расходится на два или на несколько направлений; они обозначаются зачерненными точками.

На структурной схеме все воздействия (сигналы) надписывают в изображениях по Лапласу. Однако иногда в целях упрощения их записывают сокращенно, например вместо Х_вх (р) пишут х_вх.

Непосредственно по структурной схеме (рис. 72) можно получить уравнения системы и, наоборот, по уравнениям системы можно построить структуру ную схему. Уравнения системы могут быть представлены в различной форме: операторной или дифференциальной. Для представления их в дифференциальной форме следует выполнить переход от X(р) к х(t), а операторы р и 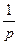соответственно заменить знаками производной и интегралом:

i

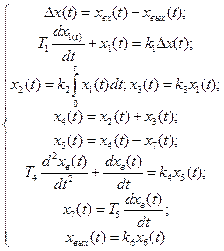
Исключением переменных можно разрешить систему уравнений (69) относительно любой переменной и обратным переходом получить передаточную функцию. Решение данной задачи будет гораздо проще, если применить непосредственно к структурной схеме правила образования передаточных функций типовых соединений звеньев, которые составляют основу структурного анализа.

Основными типами соединений звеньев в автоматических системах являются последовательное соединение, параллельное соединение и обратная связь. Все эти типы соединений звеньев показаны на структурной схеме, изображенной на рис. 72. Действительно, второе и третье звенья (интегратор и усилительное звено) соединены параллельно, а четвертое звено охвачено дополнительной обратной связью, в цепи которой включено пятое звено. Все звенья системы охвачены основной отрицательной обратной связью, что является признаком применения в системе принципа управления по отклонению. Очевидно, что при любых видах соединений линейных звеньев полученная в результате соединений система будет линейной.