Правила преобразования структурных схем н линейных систем

Операция	Исходная схема	Эквивалентная схема
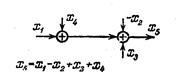
Перестановка сумматоров или элементов сравнения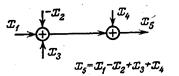
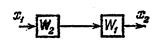
Перестановка звеньев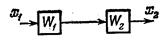
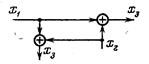
Перенос узла с выхода на вход сумматора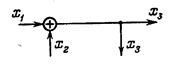
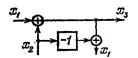
Перенос узла с входа на выход сумматора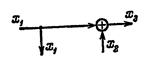
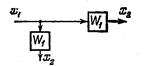
Перенос узла с выхода на вход звена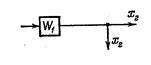
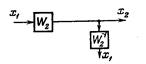
Перенос узла с входа на выход звена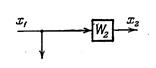
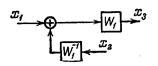
Перенос сумматора с выхода на вход звена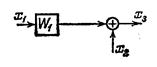
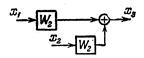
Перенос сумматора с входа на выход звена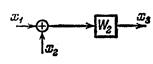
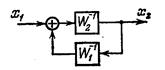
Замена звеньев прямой и обратной цепей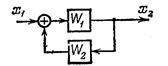
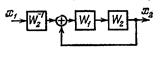
Переход к единичной обратной связи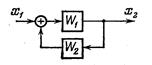

передаточные функции, определяемые выражениями

,

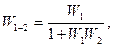
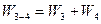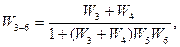
Полученная в результате преобразования схема (рис. 5.9, в) уже относится к простейшим.

Использование графов. Подобно структурным схемам графы прохождения сигналов используются для наглядного изображения математических зависимостей в системах регулирования. Графом (рис. 5.10, б) называется множество вершин и ребер. Каждому ребру соответствуют две вершины — начало и конец ребра. Вершине и ребру могут быть сопоставлены или некоторые величины, или операторы, например передаточные функции.

Основные свойства графов прохождения сигналов следующие.

1. Каждая вершина, отмеченная на графе кружком или точкой, соответствует некоторой переменной (координате) рассматриваемой системы.

2. Каждое ребро графа, изображаемое в виде линии со стрелкой, указывающей направление прохождения сигнала, имеет вершину-начало (входную величину) и вершину-конец (выходную величину). Если из вершины выходит несколько ребер, то все они имеют одинаковую входную величину.

3. Выходная величина ребра получается как результат преобразования, осуществляемого соответствующим ребру оператором, входной величины ребра.

4. Если к одной вершине подходит несколько ребер, то величина, соответствующая этой вершине, получается алгебраическим суммированием выходных величин этих ребер.

Между структурной схемой и графом прохождения сигналов имеется прямое соответствие: прямоугольник структурной схемы соответствует ребру, а линия передачи сигнала — вершине графа.

На рис. 5.10 для сравнения изображены одновременно структурная схема (а) и граф прохождения сигналов (б) одной и той же системы.

Правила преобразования графов подобны правилам преобразования структурных схем линейных систем. Эти правила изображены на рис. 5.11 В виде исходных (первый столбец) и эквивалентных (второй столбец) схем.

В дальнейшем изложении будут использоваться более удобные структурные схемы.

3. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ

РАЗОМКНУТОЙ И ЗАМКНУТОЙ АВТОМАТИЧЕСКИХ СИСТЕМ

Конечной целью структурного анализа является получение необходимых передаточных функций для последующего исследования динамики системы.

Рассмотрим структурную схему следящей системы (см. рис. 72) с единичной отрицательной связью, все звенья которой включены в прямую цепь. Структуру данной системы можно представить в виде одноконтурной (см. рис. 80, б). Для этого необходимо, в первую очередь, определить передаточную функцию разомкнутой системы по формуле последовательного соединения звеньев:

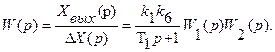
Очевидно, передаточная функция двух параллельно соединенных звеньев

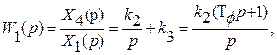
где 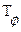= 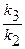- постоянная времени форсирующего звена.

Далее, необходимо определить передаточную функцию контура местнойобратной связи

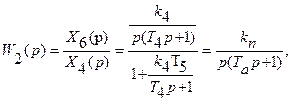
где 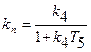- коэффициент передачи сек ^-1; 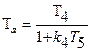— постоянная времени эквивалентного апериодического звена, сек.

Передаточная функция разомкнутой системы

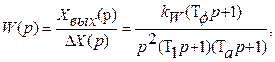(90)

где 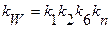— общий коэффициент передачи разомкнутой системы, сек ^-2.

В соответствии с выражением (90) на рис. 84 изображена структурная схе­ма исследуемой следящей системы, приведенная к одноконтурной.

Передаточную функцию замкнутой системы можно найти из формулы (88):

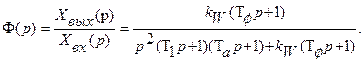
В общем случае передаточную функцию разомкнутой системы можно пред­ставить в виде отношения двух полиномов

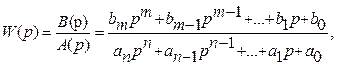(91)

причем по условию физической осуществимости системы всегда должно выпол­няться соотношение m <= п.

Передаточная функция замкнутой системы с единичной отрицательной об­ратной связью в соответствии с формулами (88) и (91)

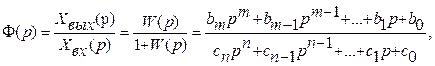
где c_i = a_i + b_i — коэффициенты характеристического полинома замкнутой системы.

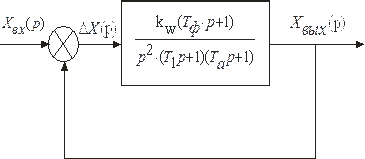Рис. 84. Структурная схема следящей системы.

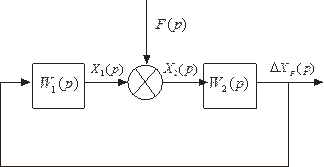Рис. 85. Структурная схема автоматической системы при действии возмущения.

Для оценки точности АС в установившихся процессах необходимо знать пе­редаточную функцию ошибки, устанавливающую связь между ошибкой и за­дающим воздействием,

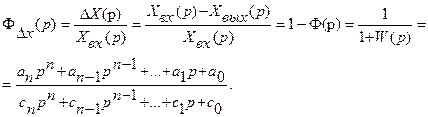(92)

Изображение ошибки

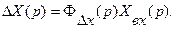
Таким образом, между передаточными функциями W (р), Ф (р) и 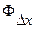(р) существуют определенные соотношения. Зная передаточную функцию разомк­нутой системы, можно определить две другие функции.

Нередко автоматические системы находятся под воздействием возмущения F (р) (рис. 85). При этом предполагается, что другие воздействия отсутствуют. Реакция на выходе системы 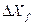(p) в этом случае является отклонением регули­руемой величины от требуемого значения — ошибкой влияния возмущения. Связь между возмущением F (р) и вызванной им ошибкой 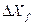(р) устанавлива­ется через передаточную функцию по возмущению, которая в соответствии с рис. 85 равна

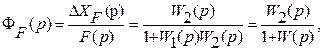(93)

где W₂ (p) — передаточная функция части системы между точкой приложения возмущения и выходом системы.

Знаменатель передаточной функции Ф_F (p) такой же, как и знаменатель других передаточных функций замкнутой системы. Если возмущение F (р) при­ложить к другой точке системы, то изменится только числитель передаточной Функции, который всегда представляет передаточную функцию соединения звеньев, заключенных между точкой приложения возмущения и выходом системы.

При действии на систему нескольких возмущений, приложенных в разных точках, реакцию системы можно найти как сумму реакций от каждого возму­щения, определенных отдельно по соответствующим формулам.