Использование структурных схем и графов

Составление основных уравнений системы автоматического регулирования (5.15) и (5.16) во многих случаях может быть значительно облегчено использованием понятия динамических звеньев. Динамические звенья были подробно рассмотрены в главе 4.

Часто систему автоматического регулирования можно рассматривать как комбинацию динамических звеньев с определенными типовыми или не типовыми передаточными функциями. Изображение системы регулирования в виде совокупности динамических звеньев с указанием связей между ними носит название структурной схемы. Структурная схема может быть составлена на основе известных уравнений системы, и, наоборот, уравнения системы могут быть получены из структурной схемы. Однако первая задача может иметь различные варианты решения (различные структурные схемы), тогда как вторая задача имеет всегда единственное решение.

Элементы структурных схем приведены в табл. 5.1.

Таблица 5.1

Наименование	Обозначение	Наименование	Обозначение
Звено с одним входом		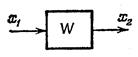Сумматор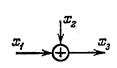
Звено с двумя входами		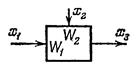Элемент сравнения (для отрицательных обратных связей)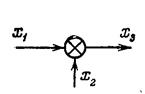
Узел (разветвление)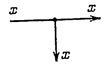

Рассмотрим вначале простейшие сочетания звеньев.

Последовательное соединение звеньев. Такое соединение показано на рис. 5.3.

Нетрудно показать, что результирующая передаточная функция равна произведению передаточных функций отдельных звеньев:

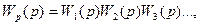(5.56)

или

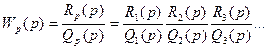(5.57)

Следует подчеркнуть, что это справедливо только в том случае, есл№ соединение выхода предыдущего звена со входом последующего не меняет-исходных уравнений каждого звена и, следовательно, его передаточной функции. В подобной последовательной цепи звеньев сигнал проходит только» в одном направлении, и она называется детектирующей цепью.

Если при соединении двух звеньев наблюдается влияние одного звена на другое, в результате которого меняются исходные уравнения какого-либо звена, то такое соединение двух звеньев должно рассматриваться как новое самостоятельное звено со своей передаточной функцией.

Параллельное соединение звеньев. Такое соединение звеньев изображено на рис. 5.4.

Так как сигналы на выходе всех звеньев складываются, то результирующая передаточная функция равна сумме передаточных функций:

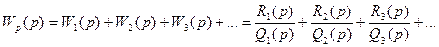(5.58)

Здесь остаются справедливыми замечания, сделанные выше относительна взаимного влияния звеньев.

Обратные связи. Такое соединение звеньев изображено на рис. 5.5. Обратная связь может быть положительной, если сигнал х₃, снимаемый с выхода второго звена, суммируется с сигналом х₁. на входе, и отрицательной, если х₃ вычитается.

Для определения результирующей передаточной функции такой комбинации звеньев запишем следующие очевидные соотношения:

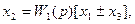
где знак плюс относится к положительной, а знак-минус — к отрицательной .обратной связи. Решая

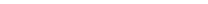эти уравнения совместно относительно х₂, можно найти результирующую»

передаточную функцию:

(5.59)

или

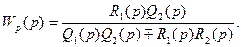(5.60)

Здесь знак минус относится к положительной, а знак плюс — к отрицательной обратной связи.

Обратные связи будут рассмотрены подробно в главе, посвященной, методам улучшения динамических свойств системы автоматического регулирования.

При использовании динамических звеньев обычно наиболее просто находится передаточная функция разомкнутой системы (рис. 5.1). Затем по формулам, приведенным в §5.2, легко находятся все уравнения системы автоматического регулирования.

При анализе системы автоматического регулирования необходимо составить ее так называемую структурную схему, представляющую собой совокупность динамических звеньев со связями между звеньями. Такая структурная схема часто является весьма простой и ее составление не представляет особого труда. Однако в некоторых случаях составление структурной схемы сопряжено с большими трудностями и может быть сделано только на основании детального анализа исходных дифференциальных уравнений системы регулирования. В этом случае структурная схема не облегчает нахождения основных уравнений системы; однако и в этом случае она остается весьма ценной, так как на ней в наглядной форме представлены все узлы исследуемой системы и все существующие между ними связи. Это может оказаться полезным во всех дальнейших исследованиях.

На рис. 5.6 в качестве примера приведена структурная схема разомкнутой системы регулирования в том случае, когда цепь регулирования представляет собой простую цепь последовательно включенных звеньев. В этом слулае передаточная функция разомкнутой системы

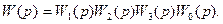(5.61)

Здесь 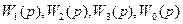представляют собой заданные передаточные функции объекта регулирования и отдельных звеньев, входящих в систему регулирования.

Нетрудно видеть, что для нахождения передаточной функции разомкнутой системы можно разомкнуть систему не обязательно так, как это показано на рис. 5.6, а в произвольном месте.

На рис. 5.7 изображен более сложный пример системы автоматического регулирования. Передаточная функция разомкнутой системй в этом случае

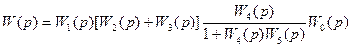(5.62)

И в этом случае для нахождения передаточной функции разомнкутой системы можно разомкнуть систему в другом месте, например в точках a, b, c или d.

Для рассмотренных на рис. 5.6 и 5.7 систем, зная передаточную функцию разомкнутой системы W(р), легко найти по формулам (5.15) и (5.16) дифференциальные уравнения для регулируемой величины и ошибки, записанные в символической форме:

,

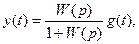
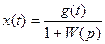где g(t) — задающее воздействие.

На рис. 5.8 изображена структурная схема системы стабилизации. В этом случае задающее воздействие g(t)=const представляет собой настройку регулятора.

Определив передаточную функцию разомкнутой системы

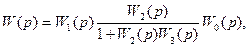(5.63)

можно по формулам (5.15) и (5.16) получить символические записи дифференциальных уравнений для регулируемой величины:

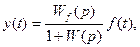
и ошибки:

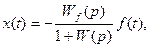
где f(t) — возмущение, действую-щее на объект, а 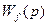— передаточная функция регулируемого объекта по возмущению.

В тех случаях, когда структурная схема оказывается сложной и содержит много различных перекрестных связей, можно попытаться ее упростить и свести к простейшему виду, например к изображенной на рис. 5.6. Преобразование структурных схем линейных систем делается на основе некоторых .правил, которые даны в табл. 5.2.

На рис. 5.9 изображены этапы упрощения сложной структурной (Схемы на основе приведенных выше правил. При упрощении введены дополнительные

Таблица 5.2