Уточнення корней

Після того, як знайдено приблизне значення корня чи визначени кордони його разположення, численними методами можна обчислити корінь з різною ступінню приближення до точного рішення. Розглянемо деякі з цих методів.

1.2.1. Метод ділення відрізка наполовину

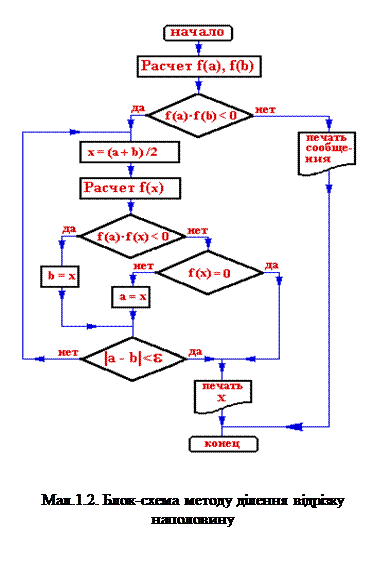
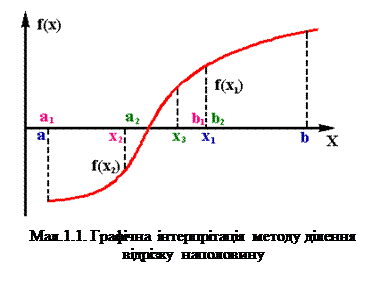Простійшим та надійним алгоритмом уточнення корня на відрізку |a,b|, якщо f(x) - неприривна функція та f(a)*f(b) < 0 , з'являється метод ділення відрізку пополам. Графічна інтерпрітація та блок-схема методу ділення відрізку наполовину доведені на мал.1.1 та 1.2. Дійсно, що середина відрізка служіть приближенням до кореня рівняння (1.1) точністю Є <(b-a)/2. У середені відрізка X₁=(a+b)/2 визначається знак функції f(X₁), потім вибираємо ту половину відрізку , на кінцях якої функція f(x) приймає значення різних знаків, та ділення повто-рюється. Якщо потрібно знайти корінь з точністю Є, то ділення відрізка наполовину продовжується до той пори, поки довжина відрізку не стане меньше 2Є. Тоді середина останього відрізку дає значення корня з потребуємою точністю.

Цей метод володіє відносно невисокою швидкістю сходження і при обчислюванні корня з високою точністю потребує значного об'єму обчислювань.Тому він частіше усього використовується для відділення корней , тобто грубого шукання, для уточнення корней приймається більш ефективні методи.

ПРИКЛАД: Методом ділення відрізка наполовину уточнити корінь рівняння

f(x)=x⁴+x²-x-0.6=0, який знаходиться у інтервалі[0.5;1.3], з точністю Є=0.15. Визначимо значення функції f(x) на кінцях інтервалу:f(0.5)=-0.79; f(1.3)=5.35. Тоді f(0.5)*f(1.3)<0; отже корінь рівняння знаходіться у цьому інтервалі.

Поділимо відрізок наполовину X₁=(0.5+1.3)/2=0.9 і визначимо значення функції у знайденої точці - f(0.9)=0.61. Так як f(0.5)*f(0.9)<0, тоді вибираємо інтервал [0.5;0.9].

Поділив новий інтервал наполовину, отримаєм X₂=0.7 і f(0.7)=-0.4. Отже корінь рівняння знаходіться у інтервалі [0.7;0.9]. Так як довжина відрізка меньш 2Є, то середина дає значення корня - x = 0.8