Метод Ньютона (доточних)
Метод Ньютона вживають до рішення рівняння f(x)=0, де f(x) безперервно-диференціьована функція. Для початку обчислювань потребується завдання начального приближення x0. Слідуючі приближення обчислюються по формулі
XN+1=XN- f(XN)/ f '(XN) ,  f '(XN)
f '(XN) 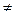 0, n=0,1,2,3... (1.2)
0, n=0,1,2,3... (1.2)
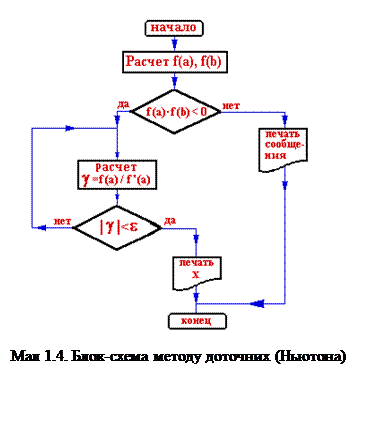
Геометрично XN+1 являється значенням абсциси точки перехрещення доточної до кривої у=f(х) у точці (xN;f(xN)) з осью абсцис, тому метод Ньютону називають також методом дотичних. Графічна інтерпрітація та блок-схема методу доточних (Ньютона) доведені на мал 1.3 та 1.4.
 У якості навчального приближення треба вибирати ту кордонну точку інтервалу, для якої знак f(x) збігається зі знаком другої похидної. У противному виподку у якості наступного приближення можна получити значення аргументу, разтошоване за межою інтервалу [а;в], та може відбутися, що процес не буде сходящим.
У якості навчального приближення треба вибирати ту кордонну точку інтервалу, для якої знак f(x) збігається зі знаком другої похидної. У противному виподку у якості наступного приближення можна получити значення аргументу, разтошоване за межою інтервалу [а;в], та може відбутися, що процес не буде сходящим.
ПРИКЛАД:
При розрахунку апарату однократно випаровування для розрахунку потребуємої температури необхідно визначити наступне рівняння:
0.01*Т3-4*Т2+180*Т+8160=0.
 З фізичних зображень виходе, що іскома температура (корінь рівняння) знаходиться у інтервалі 330-360К. Визначити ії методом Ньютону з точністю Є=0.5К
З фізичних зображень виходе, що іскома температура (корінь рівняння) знаходиться у інтервалі 330-360К. Визначити ії методом Ньютону з точністю Є=0.5К
Для розрахунку по (1.2) необхідно знайти першу похидну. Воно поравнена f '(x)=0.03*Т2-8*Т+180. Для вибору початкого приближення перевіримо знаки функції та її другої похидної. В точці x =360 f(x)=21120 >0, f ''(x) = 0.06*Т-8 = 3.6>0; відповідно, цю точку можна використовувати у якості навчального приближення.
Використовую(1.2) послідовно обчислюємо
x1=x0-(f(x0)/f '(x0))=360-(21120/1188)=342.22
x2=x1-(f(x1)/f '(x1))=342.22-(2093/955.7)=340.03 |x2-x1|>Є
x3=x2-(f(x2)/f '(x2))=340.03-(2909/928.4)=340 |x3-x2|<Є
відповідь: Т=340К
1.2.3. Метод хорд (сікучих)
У методі Ньютона на кожному кроці треба обчислювати значення функції та похидної. На практиці частіше використовують методи, які потребують обчислювання тільки значення функцій. Одним з таких методів являється метод хорд.
Цей метод заснован на допущені, що на досить малому відрізкі функція y=f(x) змінюється лінійно. Тоді криву y=f(x) на цьому відрізкі можна змінити хордою та у якості приближного значення корню прийняти точку перехрещення хорди з осью абсцис.
Графічна інтерпрітація та блок-схема методу доведені на мал. 1.5 та 1.6.
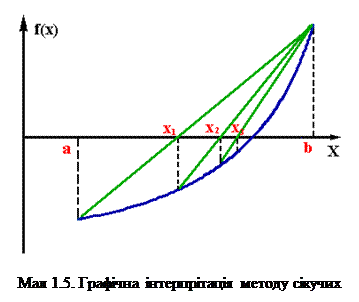
Проведемо пряму крізь точку з координатами (a, f(a) і b, f(b)), (де а та в –- конці інтервалу, які содержать корінь), знайдемо точку перехрещення цієї прямої з осью абсцис.
x1=a-(f(a)/(f(b)-f(a))*(b-a)) (1.3)
Знайдене значення х1 можна приймати за нову (ліву чі праву — в залежності від знаку f(x1) кордону скорочуванного інтервалу. Знайшовши значення f(x1) приближення відзначається виразом |xN+1-xN| <Є,
де Є - задана точність.
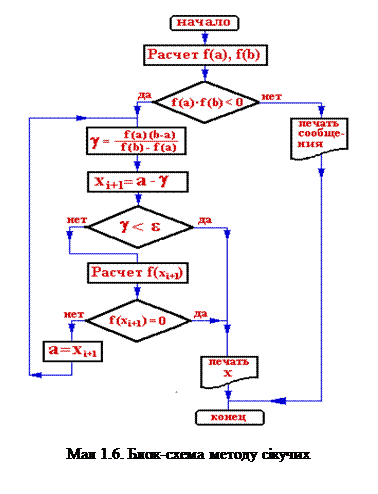 Формула (1.3) описує метод сікучих в особливості для функцій, мающих невилику кривизну.
Формула (1.3) описує метод сікучих в особливості для функцій, мающих невилику кривизну.
ПРИКЛАД.
Для визначення концентрацій компоненту на тарілці ректифікаційної колони необхідно вирішити наступне рівняння:
х3 - 0.4*x2 + 0.9*x - 0.36 = 0
Іскома величина лежить у інтервалі (0.2;0.5). Визначити її з точністю Є=0.0005.
Обчислимо значення функції на кінцях інтервалу: f(0.2) = -0.188; f(0.5) = 0.115
По формулі (1.3) знайдемо значення х:
x1=0.2 - 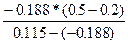 = 0.386
= 0.386 

Потім визначимо f(x). Так як f(x1) = -0.015, то корінь рівняння лежить у інтервалі |0.386;0.5|. Знайдемо наступне приближення х2:
x2=0.386- 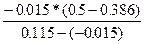 = 0.399
= 0.399
Так як |х2-х1|>Є, то повторимо процедуру. Значення f(x2)=-0.0011 та x3=0.4.
Оскільки |х3-х2|<Є,то рішення знайдене. Відповід : х=0.4
1.2.4. Метод ітеграцій (метод послідовніх приближень)
Одним з найбільш разповсюджених методів уточнення корней рівняння при рішенні завдання хімічної технології являється ітераційний метод чи метод послідовних приближень.
Метод простої ітерації використовується для рішення нелінійного рівняння з виділиним лінійним членом вигляду
x=U(x) (1.4)
та полягає у побудуванні послідовності х , починая з деякого заданого навчального значення х, за правилом
xn+1=U(Xn) , n = 0,1,2,3.... (1.5)
Якщо U(x) - непреривна функція, а Xn- сходяща послідовність, то значення
x*=lim (xn)
n 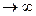
являється рішенням рівняння (1.4)
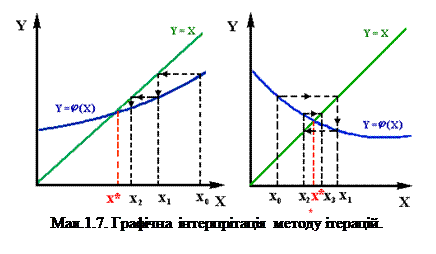
Побудування декільких послідовних приближень по (1.5) доведено на
мал. 1.7
Перетворення рівняння з метою виділення лінійного члена можна провести різними шляхами. Наприклад, якщо f(x)=x2-c=0, то можна:
а) додати до правоі чи лівої частини х: x=x2+x-c
б) поділити усе вираження на х: х=с/х і т.п.
Умови збіжності. Якщо |U'(x)|<1 , то процес сходиться, якщо ж |U'(x)|>1,
то розходиться. Нерівність треба виконувати для усіх х, обчіслюванних у ході рішення завдань.
Збіжність методу ітерацій залежить від вибору вигляда рівняння з виділе-ним лінійним членом. При невдачному виборі можна получити розходящий процес.
ПРИКЛАД:
Для визначення оптимальної концентрації компоненту у реакторі необхідно вирішити рівняння: x3+x=1000. З дослідних даних маємо, що іскома величина знаходиться у межах [9;10]. Уточнити корінь рівняння з точністю Є=Е-4.
Вихідне рівняння можна записати у вигляді:
x3=1000-x (a) чи x=(1000-x)1/3 (б).
Проналізуємо отримане рівняння. Рівняння (а) не підходить, т.я. |U’(x)| = |-2x 3| > 1. Для рівняння (б)
U'(x)= 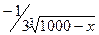
 < 1
< 1
Обчислюємо послідовні приближення Xn по формулі
Yn = 1000 - Xn ; Xn+1= (Yn) 1/3 (n=0,1,2,3...).
Знайдені значення (обчисленні з одним запасним знаком) доведені у табл.
| n | Xn | Yn |
| 9.96655 | 990.03345 | |
| 9.96666 | 990.03334 | |
| 9.96667 |
Виходячи з того, що |X3-X2|<Є , можна прийняти х = 9.96667
2. ЧИСЛЕННЕ РІШЕННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАІЧНИХ РІВНЯНЬ
Хай дана система N лінійних алгебраічних рівнянь з N невідомими
a11*x1 + a12*x2 +.....+ a1N*xN = b1
(2.1)
a21*x1 + a22*x2 +.....+ a2N*xN = b2
...................................
aN1*x1 + aN2*x2 +.....+ aNN*xN = bNN
чи у матричному вигляді
AX=b (2.2)
де
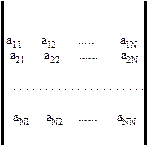
|
А = (aij) = - матриця коефіцієнтів,

 ,
, 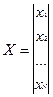 - стовпець вільних членів та стовпець невідомих відповідно.
- стовпець вільних членів та стовпець невідомих відповідно.
Коефіцієнти системи (2.1) характеризуються двома індексами. Перший індекс – і визначає номер строки, другий – j – номер стовпця.
Рішення системи (2.1) визначає знаходження таких значень невідомих, при підстановці яких у ісходну систему кожне з рівнянь перетворюється у тотожність.
Якщо матриця A неособлива , то
¦ a11 a12 .....a1N¦
¦ ¦
¦ a21 a22 .....a2N¦
detA = ¦ ................... ¦ 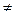 0
0
¦ aN1 aN2.....aNN¦
то система (2.1) має одиничне рішення.
Способи рішення систем лінійних рівнянь (СЛУ) у основному ділять ся на дві групи .
1. Точні методи, які уявляють собою кінцеві алгоритми для обчислюван ня корней системи (правило Крамера, метод Гауса, метод головних елементів, метод квадратних корней та інші ).
2. Ітераційні методи, які дозволяють одержувати корні системи з заданою точністю шляхом сходящих безконечних процесів (метод ітерацій, метод Зейделя, метод релаксаціє).
Дата добавления: 2015-08-26; просмотров: 809;
