Метод Гаусса.

Найбільш розповсюдженим методом рішення систем алгебраічних рівнянь являється метод Гаусса, у основі якого лежить ідея послідовного виключення невідомих. Існують різні обчислюванні схеми, реалізующі цей метод.Розглянемо одну з них – схему єдиного ділення.

Хай задана система лінійних рівнянь n-го порядку, детермінант якоє відмітний від нуля. Припустимо, що матриця коєфіцієнтів не має нульових діагональних елементів. Якщо такі маються, то відповідною перестановкою рядка їх завжди можна зробити ненульовими.

Метод Гаусса заключається у наступному:

1. З усіх рівнянь, крім першого, виключаються члени, які содержать x₁. Для цього з другого, третього,....., n-го рівнянь системи почленно, включая праві частини, віднімаються перше рівняння, діленне на а₁₁ та помножене відповідно на а₂₁, а₂₂, а₂₃,....., а_n1. У результаті цієї операції порядок усіх рівнянь, за виключенням першого, понижується на одиницю.

2. Знову полученне друге рівняння ділиться на а₂₂ та аналогичним способом, починая з третього рівняння, виключаються усі елементи, які містять х₂.

3. Повторюємо цю процедуру n-1 раз, тобто кожен раз виключая невідомі з нижчерозташованих рівнянь, можна получити у результаті ступенчату трикутникову систему рівнянь, еквівалентну першоначальноє, останнє рівняння якої отримує тільки одну невідому.

4. Рішення ступенчатої системи рівнянь здійснюється шляхом послідовного обчислювання невідомих, починая з останього рівняння.

ПРІКЛАД:

Для визначення змісту компонентів начальної суміші необхідно визначити наступну систему рівнянь :

2.0*x₁+1.0*x₂-0.1*x₃= 3.7

0.4*x₁+0.5*x₂-4.0*x₃=13.4

0.3*x₁-1.0*x₂+1.0*x₃= 1.3

Для рішення системи використовуємо метод Гаусса. З другого та третього рівняння виключимо члени, які містять х₁. Для цього спочатку поділимо перше рівняння на а₁₁ = 2.0. Отримаємо:

х₁+0.5*x₂-0.05*x₃=1.85

Потім, помножимо отримане рівняння на а₂₁ та а₃₁, віднимимо з друго го та третього рівняннь відповідно. Таким чином отримаємо систему з двома невідомими:

0.3*x₂+4.02*x₃=12.66

-1.15*x₂+1.015*x₃=0.745

Поділив перше рівняння отриманої системи на а₂₂ та помножив його на а₃₂, вичтемо з другого рівняння цієї системи.

16.425*x₃=49.275

Таким чином,еквівалентна система має вигляд:

x₁ + 0.5*x₂ - 0.05*x₃ = 1.85

x₂+ 13.4*x₃ = 42.2

16.425*x₃ = 49.275

З отриманої еквівалентної системи послідовно знайдемо:

x₃ = 3.0

x₂ = 42.2 - 13.4*3.0 = 2.0

x₁ = 1.85- 0.5*2.0 + 0.05*0.3 = 1.0

Процес побудування еквівалентної трикутної системи називається прямим ходом, а процес знаходження значень невідомих – оберненим ходом.

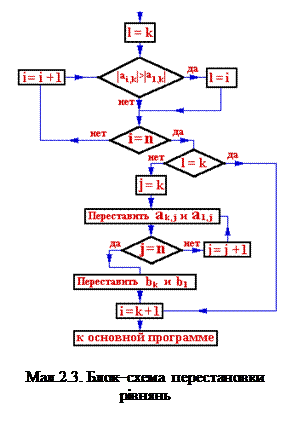
2.3 Блок-схема програми для рішення систем лінійних рівнянь методом Гаусса

Блок-схему програми можна поділити умовно на три частини. Перша – реалізує алгоритм виключення невідомих; друга - оберненой підстановки; третя - визначає найбільший коефіцієнт при Х та перестановці рівняння при необхідності.

У блок-схемі усі множники обозначаються одним та тим же символом m. Якщо обчислювання у програмі вірно організовані, то кожному етапі обчислювань не потребує більш одного множника.

При аналізі блок – схеми треба чітко представити зміст індексів i,j,k.

k – визначає номер того рівняння, яке віднімається з останніх, а також номер того невідомого, яке виключається з останніх n – k рівнянь.

i – означає номер рівняння, з якого у цю мить виключається невідомі.

j – означає номер стовпця.

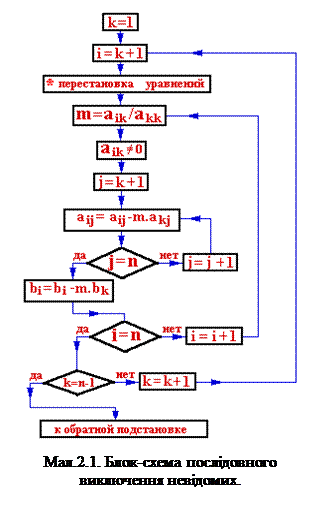Блок-схема послідовного виключення невідомих доведена на мал.2.1.

Зворотня підставлення для находження значення невідомих задається наступними формулами:

x _N = b ^N-1_N / a ^N-1_NN

x_N-1=[ b ^N-2_N-1 - a ^N-2_N-1,N * x_N ] / a ^N-2_N-1.N-1

.....................................

x_j = [b ^j-1_j - a ^j-1_jn * x_n -...- a^j-1_j,j+1 *x_j+1] / a ^j-1_jj

для j = n-2, n-3, ..., 1.

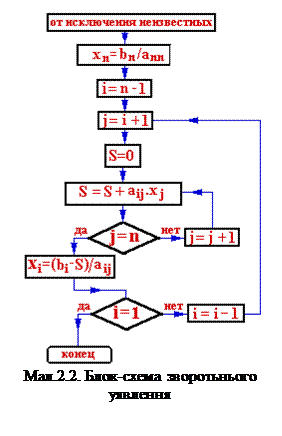
Блок-схема зворотьнього уявлення доведена на мал.2.2. Помітимо, що у блок–схемі (мал.2.1) усі індекси у процесі обчислювання збільшуються, а у блок-схемі (2.2) один з індексів, а саме i, зміньшується.

Розглянемо третью блок-схему перестановки рівняння (2.3) яка входить у блок–схему (2.1). Завдання знаходження найбільшого коефіцієнта при x_k та перестановці рівнянь при необхідності зв'язана з зменшенням помилки округлення, яка виникає при обчислюванні з числами з плаваючою комою. По–перше, перестановка може бути потрібна, щоб a_kk 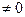– щоб ухилитися від ділення на 0. А також, використовувая перестановку, можливо зменшення помилки округлення. Спочатку розглянемо числовий приклад. Розв'яжемо систему методом включення підставних:

3.241*10²*x₁+1.600*10²*x₂=1.632*10²

1.020*10⁴*x₁+1.540*10³*x₂=1.174*10⁴

Точне рішення ціє системи наступне:

x₁=1.000*10⁰ ; x₂=1.000*10⁰ ;

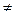Рішив це рівняння метод виключення у тому порядку,у якому вони записані, використовуя при обчисленні числа з 4 значними цифрами у мантісе. Так як а ₁₁ 0, то можна рішити по відомой схемі.

Перший та єдиний множник:

1.020*10⁴

m = --------------- = 3.147*10³

3.241*10⁰

Перетворене друге рішення має вигляд:

5.730*10^-1*x₁-5.020*10⁵*x₂ = -5.019*10⁵

Коефіцієнт при х₁ повинен був бути = 0, але помилка округлення не дозволяє

отримати точний результат.Так як цей коефіцієнтів нікуди не входе у подальшому обчислюванні,то приймаємо його равним 0 та утворюємо зворотню підстановку:

-5.019*10⁵

x₂ = --------------- = 9.998*10^-1

-5.020*10⁵

З першого одержуємо : x₁ = 9.873*10^-1

Зараз підставим рівняння так, щоб максимальний по модулю елемент попав на

головну діагональ:

1.020*10⁴*x₁+1.540*10³*x₂=1.174*10⁴

3.241*10⁰*x₁+1.600*10²*x₂=1.632*10²

Зараз множник

3.241*10⁰

m = --------------- = 3.177*10^-4

1.020*10⁴

Перетворенне друге рівняння: 0.000*x₁+1.595*10²*x₂=1.595*10²

Звідки x₂ = 1.000*10⁰ ; x₁=1.000*10⁰

У цьому прикладі коефіцієнти дуже відрізняються по величині, але частіше ці різниці не так великі. Однак при рішенні великої системи рівнянь помилки округлення можуть накоплюватися та відповіді можуть не містить ні одної вірної цифри. Тому при рішенні СЛР на ЕОМ методом виключення повинно передбачити можливість перестановки рівнянь.

Отже, завдання зводиться до перестановки n-k+1 останніх рівнянь, так щоб найбільший по модулю коефіцієнт при x_k попав на головну діагональ.

Описаний спосіб рішення СЛР називають методом головного елементу.

При розгляденні блок–схеми необхідно пам'ятати, що при переході до даного етапу обчислюваний індекс k має деяке визначене значення, а i = k+1.

1. Спочатку у програму вводиться допоміжний індекс l , якому присвовується значення k.

2. Перше порівняння виробляєтьса між а_к,l елементом, який лежить на головній діагоналі, та наступним за ним a_i,k. Якщо |a_i,k|>|a_l,k|, то індексу l присвоювають значення i та подальше порівняння виконується з другим елементом.

Тому індекс lявляється номером елементу, який з'явився при порівнянні більш других по модулю. Індекс і пробігає по ходу програми значення від k+1 до n включно, та у кінці цього циклу індекс lвизначає номер найбільшого по модулю елементу у k-ому стовпці. При перестановці рівняння цей коефіцієнт повинен попасти на головну діагональ.

Може статися так, що значення а_і,к вже являється найбільшим по модулю елементом. Тому така можливість відразу перевяється і у тому випадку перестановка не проводиться.

Фактично процес полягає у перестановці коефіцієнтів, один з яких утримується у рівнянні k, а другий - у рівнянні l, яким би не було значення l.

Перестановку можна провести за допомогою трьохступеневого процесу. Цю перестановку необхідно виробити для усіх пар коефіцієнтів двох рівнянь:

DO j=k TO N; TEMP=A(k,j); A(k,j)=A(l,j); A(l,j)=TEMP; END;

Аналогічно для в.

Перед поверненням до основного процесу обчислювань необхідно відновити первісне значення індексу і, який був використован при порівнянні. Так як перед початком процесу індекс і мав значення k+1, то наприкінці блоку йому присвоюєтся попереднє значення i=k+1.

2.4. Метод простій ітерації

При великому числі невідомих лінійної системи схема метода Гаусса, яка дає вірне рішення, становиться дуже громіздкой. У цьому випадку для знаходження корней системи іноді краще користуватися приближеними обчислюваними методами - ітераційними. Пріваблівім у Ітераційних методах є іх властивість самовиправляємости та простота реалізації на ЕОМ.

Хай дана система лінійних алгебраічних рівнянь.

А*X=b (2.3)

з неособливою матрицею. Щоб використувати до неї метод ітерацій, необхідно довести її до вигляду

X=C*X+f (2.4)

де С - деяка матриця, а f - вектор-стовпець.

Ітераційний процес для початку обчислювання потребує завдання навчальних умов. Виходя з довільного вектора Х

x⁰₁

x ⁰ = x⁰₂

....

x⁰_N

будуємо ітераційний процес:

X^(к+1) = c*X ^(к) + f (k=0,1,2,....) (2.5)

Зробивши ітераціі, отримаємо послідовність векторів x⁽¹⁾, x⁽²⁾, х ⁽³⁾,..., x^(к) .

Якщо послідовність приближення має межу, то ця межа є рішенням системи (2.3)

lim ( x^(к+1) )=c * x^(к) + f (2.6)

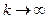
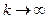
Процес ітерації закінчується, коли |x ^(к+1) - x^(к) | < Є, де Є - дана точність рішення.

Процес ітерацій (2.5) добре зходиться (тобто чісло приближення, необхідне для отрімання корнів системи (2.3) з заданою точністю невелико), якщо елементи матриці А малі по абсолютній величині. Іншими словами для успішного використовування методу ітерацій модулі діагональних коефіцієнтів системи (2.3) повинні бути більш суми модулів

останніх коефіцієнтів рівняння (вільние члені не враховується). Ця умова являється умовою сходження.

Відмітимо одну з важливих особливостей методу ітерацій. Сходячийся процес ітерації обладає властивостями самовиправлення, тобто окрема помилка в обчисленнях не відображується на кінцевому результаті, так як помилкове приближення можна розглядати як нове навчальне приближення.

Начальний вектор x може бути вибран довільно. Іноді беруть x⁽⁰⁾ = f ⁽⁰⁾ . Найбільш доцільно як компоненту начального вектора увзяти приближенне значення невідомих, отриманих грубою прикидкою. Ніж ближче початкове приближення до значення корней системи, тим швидкіше зійдеться ітераційний процес .

Якщо матриця А неособлива, то систему (2.3) за допомогою сукупності елементарних перетворень завжди можна привести до вигляду (2.4).

До елементарного переворення матриць відносяться :

а) заміна рядків (стовпців);

б) множення усіх елементів якого-небудь рядка (стовпця) на одне і те ж число, відмінне від нуля;

в) додання до елементів якого-небудь рядка (стовпця), відповідних елементів другого рядка (стовпця), множенних на одне і те ж число.

Практично діють наступним чином. З заданой системи виділяють рівняння з коефіцієнтами, модулі яких більше суми останніх коефіцієнтів рівняння. Кожне віділене рівняння виписують у такий рядок нової системи, щоб найбільший по модулю коефіцієнт опинився діагональним. Потім, використючи елементарні перетворення, складають останні рівняння нової системи. При цьому необхідно, щоб були викорисовані у тому чи іншому сполученні усі рівняння початкової системи.

ПРИКЛАД:

Для знаходження коефіцієнтів емпирічної залежності необхідно визначити наступну систему рівняння

2*x₁-0.5*x₂+4*x₃=22 (A)

3*x₁+3.5*x₂+3*x₃=35 (Б)

x₁+0.5*x₂-x₃=-1 (B)

У рівнянні (А) коефіцієнт при х₃ по модулю більш суми модулей останніх коефіцієнтів, тому можна приймати це рівняння за третє рівняння нової системи. Щоб отримати друге рівняння з максимальному по модулю коефіцієнтом при х₂, достатньо скласти разність (Б)-(А):

х₁+4*x₂-x₃=13

При перетворенні початкової системи до вигляду (2.4) були використані рівняння (А) та (Б). Отже, у перше рівнняня обов'язково повинно увійти рівняння (В), наприклад, використовуючи наступне перетворення

(А)+4*(В): 6*x₁+1.5*x₂+0*x₃=18.

Таким чином, отримана еквівалентна система рівнянь,котра задовольняє умовам сходження:

6*x₁+1.5*x₂=18 (А1)

x₁+4*x₂-x₃=13 (Б1)

2*x₁-0.5*x2+4*x₃=22 (В1)

Вирішуя перше рівняння відносно х₁, друге - відносно х₂, третє - відносно х₃, отримаємо

x₁=3-0.25*x₂

x₂=3.25-0.25*x₁+0.25*x₃ (2.7)

x₃=5.5-0.5*x₁+0.125*x₂

Як навчальний вектор x⁽⁰⁾ візьмемо елементи стовбця вільних членів, округляючи їх значення до одного знаку після коми:

x⁽⁰⁾₁= 3; x⁽⁰ ₂ = 3.3; x⁽⁰⁾₃ = 5.5.

Точність обчислювання Є=0.01

Послідовно обчислюємо:

при k=1:

x⁽¹⁾₁ = 3 - 0.25*3.3 = 2.175

x⁽¹⁾₂ = 3.25 - 0.25*3 + 0.25*5.5 = 3.875

x⁽¹⁾₃ = 5.5 - 0.5*3 + 0.125*3.3 = 4.413

при k=2:

x⁽²⁾₁ = 3 - 0.25*3.875 = 2.031

x⁽²⁾₂ = 3.25 - 0.25*2.175 + 0.25*4.413 = 3.810

x⁽²⁾₃ = 5.5 - 0.5*2.175 + 0.125*3.875 = 4.897

та т.д.

Результати подальших обчислювань доведені у таблиці.

-----------------------------------------------------------------------

k | 0 | 1 | 2 | 3 | 4 | 5 | 6

-----------------------------------------------------------------------

x1 3 2.175 2.031 2.048 2.009 2.006 2.002

x2 3.3 3.875 3.810 3.966 3.978 3.991 3.997

x3 5.5 4.13 4.897 4.961 4.972 4.993 4.996

-----------------------------------------------------------------------

Так як модулі разностей значень Х^(к) при k=5 і k=6

| x⁽⁶⁾₁ - x⁽⁵⁾₁ | = 0.004; | x⁽⁶⁾₂ - x⁽⁵⁾₂ | = 0.006; | x⁽⁶⁾₃ - x⁽⁵⁾₃ | = 0.003;

меньш заданої точності Є, то як рішення приймаємо:

х₁ = 2.002 ; х₂ = 3.997 ; х₃ = 4.9967.

Для порівняння точні значення невідомих: х₁ = 2; х₂ = 4; х₃ = 5.