Тема 34 Определение скорости и расхода при истечении жидкости из малого незатопленного отверстия в тонкой стенке при постоянном напоре

Малым называется отверстие, в разных точках которого геометрический напор Н[1] практически одинаковый. При выполнении этого условия скорости на верхней и нижней границах вытекающей из отверстия струи можно считать одинаковыми. Для малого отверстия, расположенного в вертикальной плоскости наибольший вертикальный размер S не превышает 0,1 Н (S £ 0,1 Н).

Тонкой называют стенку, если её толщина не влияет на условия истечения. Вытекающая жидкость касается только кромки отверстия. Струя, вытекающая из отверстия, преодолевает лишь местные сопротивления. Это может быть обеспечено либо при толщине стенки d £ (0,2…0,5)×d, либо срезом кромок под острым углом (при d < 3d). У тонкой стенки отверстие имеет острую кромку.

Рассмотрим истечение жидкости плотностью r из резервуара через малое незатопленное отверстие диаметром d. Глубина погружения центр тяжести отверстия под уровень свободной поверхности (напор) равна Н.

Истечение происходит при постоянном напоре. При постоянном напоре скорости истечения будут неизменны во времени, то есть движение будет установившимся.

Пусть свободная поверхность жидкости в резервуаре находится под давлением р₀. истечение происходит в газовую среду с давлением р_с через незатопленное отверстие с острой кромкой (рис. 58).

Траектории частиц при приближении к отверстию искривляются. Действующая центробежная сила направлена внутрь формирующейся струи. Сечения струи постепенно уменьшаются. Сжатие продолжается и на некотором расстоянии от плоской стенки после выхода струи из резервуара. Движение жидкости на этом участке вблизи стенки неравномерно. Живые сечения потока на этом участке криволинейные, постоянно уменьшающиеся. По мере удаления от отверстия кривизна линий тока уменьшается, и на некотором расстоянии от стенки движение приближается к плавно изменяющемуся.

Рисунок 58

Ближайшее к отверстию сечение струи, в котором движение может быть принято плавно изменяющимся (течение приобретает почти параллельно-струйный характер) называется сжатым сечением. Для круглых отверстий сжатое сечение (сечение С-С) находится на расстоянии примерно [l » (0,5…1)×d] от внутренней поверхности стенки резервуара.

Скорости во всех точках сжатого живого сечения С-С можно считать параллельными и в силу малости отверстия одинаковыми, равными v_c.

Коэффициент сжатия струи есть отношение площади сжатого живого сечения w_с к площади отверстия w:

e = 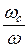(34.1)

Ниже сжатого сечения площади живых сечений струй изменяются слабо, и жидкость движется в виде компактной струи. На достаточно большом расстоянии от отверстия в связи с насыщением струи воздухом (аэрация) струя начинает дробиться и теряет компактность.

Чтобы получить формулы для определения скорости и расхода, составим уравнение Бернулли для сечений А-А и С-С (в резервуаре и сжатом сечении струи соответственно). Горизонтальную плоскость сравнения проведём через центр сжатого сечения. Тогда

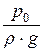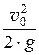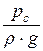Н + + a₀ × = 0 + + a_с × 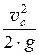+ h_пот. (34.2)

Потери удельной энергии (в данном случае потери на острой кромке) выразим как

h_пот = z_ос × ,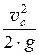

где z_ос – коэффициент сопротивления при истечении из отверстия в тонкой стенке с острой кромкой.

Перенеся известные величины в левую часть уравнения (34.2), получим

Н + 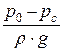= 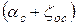× 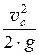- a₀ × .

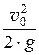Учитывая, что по уравнению неразрывности v_c ´ w_с = v₀ ´ w₀ или, с учётом уравнения (34.1) v_c × e × w = v₀ × w₀ (w₀ – площадь сечения резервуара А-А), имеем

Н + = × .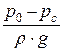

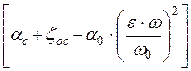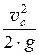Отсюда в общем случае средняя скорость истечения (в сжатом сечении) равна:

v_c = × .

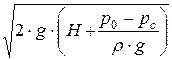или

v_c = j₀ × 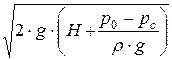. (34.3)

где j₀ - коэффициент скорости.

j₀ = . (34.4)

Коэффициент скорости j₀ отражает влияние распределения скоростей в сжатом сечении (коэффициент Кориолиса a_с), потерь напора (коэффициент z_ос) и соотношение площадей в сжатом сечении w_с и в сечении резервуара А-А w₀ .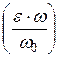

Определим расход истекающей жидкости с учётом выражения (34.1)

Q = w_с × v_c = e × w × v_c.

Используя выражение (34.3), получаем

Q = e × w × j₀ × .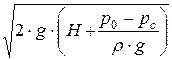

Произведение коэффициента сжатия e и коэффициента скорости j₀ называется коэффициентом расхода m₀:

m₀ = e × j₀. (34.5)

Окончательно имеем

Q = m₀ × w × 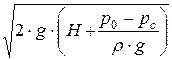. (34.6)

В большинстве случаев на практике происходит истечение в атмосферу (р_с = р_бар) из сосудов или резервуаров, на свободной поверхности которых р₀ = р_бар, то есть р_с = р₀ = р_бар.

При р_с = р₀ формулу для средней скорости в сжатом сечении (истечения) (34.3)

получают в виде

v_c = j × 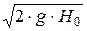, (34.7)

где Н₀ = Н + a₀ × 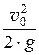- напор с учётом скоростиподходаv₀;

j - коэффициент скорости.

j = 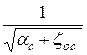. (34.8)

Коэффициент скорости j отражает влияние распределения скоростей в сжатом сечении (коэффициент Кориолиса a_с) и потерь напора (коэффициент z_ос).

Для расхода запишем

Q = w_с × v_c.

С учётом формул (34.1) и (34.7) имеем

Q = e × w × j × .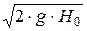

Коэффициент расхода m равен произведению коэффициента сжатия e и коэффициента скорости j:

m = e × j. (34.9)

Получаем выражение для расхода истекающей жидкости:

Q = m × w × 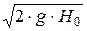. (34.10)

В невязкой (идеальной) жидкости сопротивления отсутствуют: h_пот = 0; z_ос = 0; a_с = 1; j = 1. При движении вязкой жидкости имеются потери удельной энергии: h_пот ¹ 0; z_ос > 0; a_с > 1; j < 1. Обычно условно принимается a_с = 1, хотя распределение скоростей в пределах сжатого сечения, строго говоря, неравномерное.

В тех случаях, когда можно пренебречь влиянием соотношения площадей w_с = e × w к w₀ или влиянием скоростного напора a₀ × 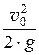, в расчётах используется только коэффициент скорости j (формула 34.8) и коэффициент расхода m (формула 34.9). Тогда основные расчётные формулы принимают вид

v_c = j × 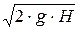; (34.11)

Q = m × w × 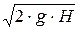. (34.12)

Коэффициент скорости j характеризует уменьшение скорости истечения реальной жидкости по сравнению со скоростью истечения в таких же условиях идеальной жидкости. Уменьшение скорости происходит вследствие потерь напора при прохождении жидкости через отверстие, а также вследствие потерь напора, имеющих место при расширении сжатой струи. Численно коэффициент скорости определяется как отношение действительной скорости истечения реальной жидкости к теоретической скорости (максимально возможной) v_max = 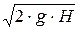, характеризующей истечение идеальной жидкости

j = 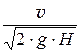= 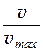, (34.13)

где v_max – максимальная (теоретическая) скорость истечения идеальной жидкости.

v_max = 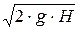. (34.14)

Коэффициент расхода m характеризует уменьшение расхода реальной жидкости по сравнению с расходом в таких же условиях идеальной жидкости.

Коэффициент расхода равен отношению действительного расхода, соответствующего истечению реальной жидкости, к теоретическому (максимальному) расходу истечения в таких же условиях идеальной жидкости

m = 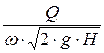= 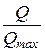. (34.15)