Тема 37 ИСТЕЧЕНИЕ ЧЕРЕЗ МАЛОЕ ЗАТОПЛЕННОЕ ОТВЕРСТИЕ
При истечении через отверстие под уровень жидкости отверстие называется затопленным. Рассмотрим истечение через затопленное отверстие (рис. 1) при условии, что положение свободных поверхностей жидкости по обе стороны от отверстия не изменяются во времени, давление на свободной поверхности до отверстия и за ним атмосферное рбар.
Запишем уравнение Бернулли для сечений А-А и В-В, совпадающих со свободной поверхностью до отверстия и за ним:

z1+ 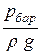 + a1
+ a1 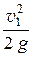 = = z2 +
= = z2 + 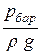 + a2
+ a2 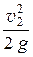 + Dhпот.
+ Dhпот.
Плоскость сравнения 0-0 проведем через центр отверстия. Пренебрегая скоростными напорами в сечениях А-А и В-В вследствие их малости получим
z1 = z2 + Dhпот
или
z = Dhпот,
где z – разность (перепад) уровней жидкости до отверстия и за ним. z = z1 - z2;
Dhпот = åz 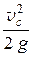 ,
,
где vc – средняя скорость в сжатом сечении С-С затопленной струи.
Между сечениями А-А и В-В должны быть учтены потери напора:
а) потери между сечениями А-А и С-С, аналогичные потерям при истечении в атмосферу через малое отверстие с острой кромкой:
hо.к. = zо.к. 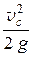 ;
;
б) потери между сечениями С-С и В-В, связанные с внезапным расширением струи от сжатого сечения до сечения во втором резервуаре, равные:
hв.р. = aс 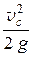 ;
;
Соответственно скорость в сжатом сечении равна:
vc = 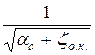
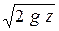
или
vc = j 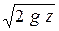 ,
,
где j - коэффициент скорости.
Так как площадь струи в сжатом сечении равна wс = e w, то расход, проходящий через затопленное отверстие равен:
Q = e j w 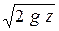
или
Q = m w 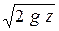 ,
,
где e - коэффициент сжатия струи;
w - площадь отверстия;
m - коэффициент расхода.
Опыты показывают, что коэффициент расхода m при истечении через затопленное отверстие может приниматься равным коэффициенту m для незатопленного отверстия.
Дата добавления: 2015-08-26; просмотров: 1090;
