Тема 45 ТЕПЛОВОЕ СОПЛО
Рассмотрим цилиндрическую трубу (площадь поперечного сечения w = const) с теплопроницаемыми стенками (Qт ¹ const), по которой движется газ с постоянным массовым расходом (Qm = const).
Для получения уравнения, связывающего изменение теплового потока Qт по длине сопла и изменение скорости v воспользуемся уравнением состояния:
р = r×R×T,
где r – плотность газа, кг/м3;
R – газовая постоянная;
Т– абсолютная температура газа;
р – абсолютное давление газа.
Дифференцируем это уравнение по x
 = R×r×
= R×r× 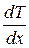 + R×T×
+ R×T× 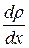 . (45.1)
. (45.1)
Изменение давления по длине по длине выразим из уравнения Эйлера v× 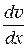 =
= 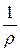 ×
×  .
.
 = - r ×v×
= - r ×v× 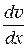 . (45.2)
. (45.2)
Уравнение неразрывности запишется 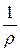 ×
× 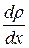 +
+ 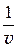 ×
× 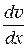 = 0. Отсюда выразим
= 0. Отсюда выразим 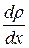 :
:
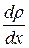 = -
= - 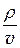 ×
× 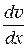 . (45.3)
. (45.3)
Введём в уравнение состояния по длине (45.1) полученные выражения (45.2) и (45.3) для  и
и 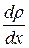
- r ×v× 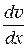 = R×r×
= R×r× 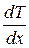 -
- 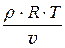 ×
× 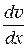 . (45.4)
. (45.4)
Преобразуем выражение
v×  ×
× 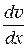 = v×
= v× 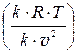 ×
× 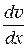 = v×
= v× 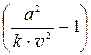 ×
× 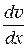 = v×
= v× 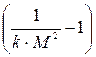 ×
× 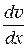 =
=
= R× 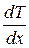 , (45.5)
, (45.5)
где k – показатель адиабаты;
а – скорость звука. a = k×R×Т;
М – число Маха. М = 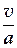 .
.
На основании первого закона термодинамики имеем
R× 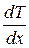 =
= 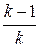 ×
× 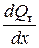 -
- 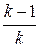 ×v×
×v× 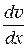 . (45.6)
. (45.6)
Подставив эти значения в уравнение состояния получим
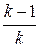 ×
× 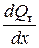 -
- 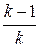 ×v×
×v× 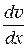 = v×
= v× 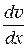 ×
× 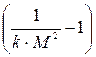 .
.
Умножив на k получим окончательную формулу
(k - 1) × 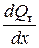 = v ×
= v × 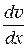 ×
× 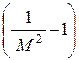 . (45.7)
. (45.7)
Так как (k - 1) всегда положителен, то:
1) Скорость потока в дозвуковой области (М < 1) будет расти, если приход тепла будет возрастать.
2) В сверхзвуковой области (М > 1), когда 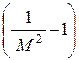 < 0, скорость будет расти при отводе тепла.
< 0, скорость будет расти при отводе тепла.
3) В критическом сечении, где М = 1, 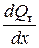 = 0.
= 0.
 Для трансформации дозвуковых скоростей в сверхзвуковые, необходимо подвод тепла осуществлять на начальном участке сопла. Тогда в некотором критическом сечении может быть создана скорость газа, равная звуковой. Если за этим сечением осуществить отвод тепла, будет получена сверхзвуковая скорость (рис. 76).
Для трансформации дозвуковых скоростей в сверхзвуковые, необходимо подвод тепла осуществлять на начальном участке сопла. Тогда в некотором критическом сечении может быть создана скорость газа, равная звуковой. Если за этим сечением осуществить отвод тепла, будет получена сверхзвуковая скорость (рис. 76).
Рисунок 76 – Схема теплового сопла
[1] расстояние по вертикали от свободной поверхности жидкости до рассматриваемой точки отверстия
Дата добавления: 2015-08-26; просмотров: 2251;
