Критические параметры. Форма сопловых и рабочих каналов

Определим расход газа через сопло, считая процесс течения в сопловом канале изоэнтропийным. Из уравнений неразрывности имеем:

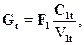
где G_t - теоретический расход через сопло;

F₁ - площадь выходного сечения сопла;

С_1t - теоретическая скорость в выходном сечении;

Vϑ_1t - удельный объем в конце изоэнтропийного процесса. Согласно уравнению (2.26)

.

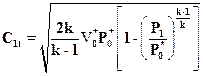При изоэнтропийном процессе:

Подставляя C_1t и V_1t в исходное уравнение, после преобразований получим:

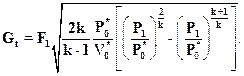(2.30)

Обозначая 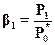имеем:

(2.31)

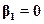Из формулы (2.31) следует, что при постоянных параметрах перед соплом расход G_t зависит от отношения давлений . При и 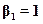расход равен нулю. Следовательно, функция 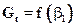имеет максимум.

Отношение давлений 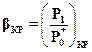при котором расход достигает наибольшего значения называется критическим. Все параметры (давление - Р_кр, скорость - С_кр, удельный объем - V_кр, температура - Т_кр), соответствующие критическому отношению давлений называются критическими.

Для определения критического отношения исследуем функцию 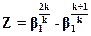, стоящую в скобках в формуле (2.31), на максимум.

Взяв первую производную и приравняв ее нулю, имеем

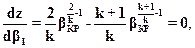
откуда критическое отношение давлений

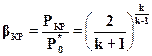. (2.32)

Из выражения (2.32) следует, что критическое отношение давлений зависит только от показателя изознтропии 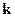и для данной рабочей среды есть величина постоянная.

Найдем максимальный расход пара G_tmax и критическую скорость С_кр. Для определения максимального расхода подставим в формулу (2.31) вместо критическое отношение давлений. Учитывая выражение (2.32), после преобразований получим

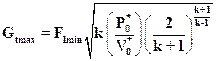, (2.33)

где F_1min - площадь минимального сечения сопла (площадь горла). Из формулы (2.33) следует, что при неизменной площади поперечного сечения сопла F_1min максимальный расход зависит только от начальных параметров и не зависит от давления за соплом.

Для определения критической скорости подставим критическое отношение давлений в формулу (2.26) и после преобразования получим

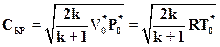. (2.34)

Выразим критическую скорость через критические параметры. Из уравнения состояния имеем

.

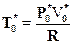При изоэнтропийном течении

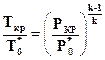
или, учитывая выражение (2.32)

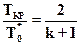. (2.35)

Подставляя в формулу (2.34) значение То*, вычисленное по формуле (2.35), получим

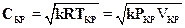. (2.36)

Скорость звука в сплошной среде определяется по выражению

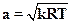. (2.37)

Из сравнения формул (2.36) и (2.37) следует, что при изоэнтропийном течении критическая скорость равна скорости звука в среде, имеющей температуру, равную критической (Т = Tкр).

На рис. 2.2 по формулам (2.31) и (2.26) и уравнению изоэнтропы построены кривые, показывающие характер изменения расхода G_1t, скорости истечения C_1t и удельного объема V_1t в выходном сечении сопла в зависимости от отношения давлений при неизменных начальных параметрах рабочего тела.

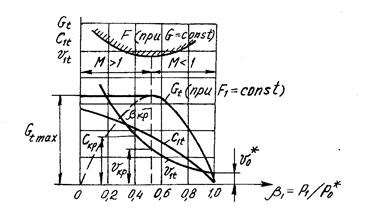
Рис. 2.2 Зависимость расхода через сопло, площади выходного сечения сопла, скорости и удельного объема е выходном сечении от отношения давлений

Из рисунка видно, что в области дозвукового истечения 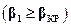при уменьшенииβ₁ (в случае уменьшения давления за соплом) расход возрастает. При критическом течении 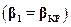расход становится максимальным. В области сверхзвукового истечения 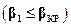согласно формуле (2.31) расход должен уменьшаться и при β1 = 0 расход должен быть равен нулю.

Опыты подтверждают увеличение расхода через сопло при уменьшении β₁ в дозвуковой области истечения, но не подтверждают снижение расхода в области сверхзвукового истечения. В действительности, достигнув наибольшего значения при критическом отношений давлений, расход через сопло в дальнейшем при всех значениях 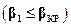остается неизменным и равным максимальному. Причина такого изменения расхода заключается в следующем. В сплошных средах скорость распространения малых возмущений равна местной скорости звука. Поэтому при понижении давления за соплом (это относится к малым возмущениям) в дозвуковом истечении происходит перераспределение давлений по длине всего сопла и в сужающейся части имеет место увеличение скорости потока. При сверхзвуковом режиме в самом узком месте сопла скорость потока становится равной местной скорости звука. Поэтому понижение давления за соплом не приводит к какому-либо перераспределению давлений по длине дозвуковой части сопла, так как малые возмущения не могут преодолеть скорость звука. При этом расход определяется площадью проходного сечения самого узкого места сопла и критическими параметрами в этом сечении. Согласно уравнению (2.7) при установившемся течении (G_1t = const)

.

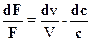Из рисунка 2.2 видно, что характерной особенностью дозвуковой области течения (М < 1.0) является более интенсивное нарастание скорости потока, чем удельного объема (dC/C > dV/V). В области сверхзвукового истечения (М > 1.0) наоборот dV/V > dC/C. По этой причине площадь проходного сечения сопла при М < 1.0 уменьшается от входа к выходу, а при М > 1.0 - увеличивается.

Из рисунка 2.2 следует, что форма сопла при дозвуковом и звуковом истечении (М < 1.0) должна быть сходящейся (суживающейся), при сверхзвуковом (М > 1.0) сходяще-расходящейся. В сходящейся части сходяще-расходящегося сопла поток расширяется от начального давления до критического, а в расходящейся - от критического до заданного давления P₁ < Р_кр.

Сходяще-расходящееся сопло называется соплом Лаваля, для краткости будем называть его в дальнейшем расходящимся (расширяющимся) соплом.

В расходящихся соплах выходное сечение не определяет расхода, так как последний зависит не от площади выходного сечения и параметров в этом сечении, а от площади и параметров узкого сечения.