Уравнение закона сохранения энергии

Рассмотрим объем газа между сечениями 0-0 и 1-1 в момент времени τ=0 (рис.2.1). Условимся записывать работу и теплоту со знаком плюс в случае их подвода к газу и со знаком минус в случае отвода. Теплота трения всегда подводится к газу. По истечении бесконечно малого отрезка времени газ займет новое положение . При этом, в общем случае, будет подведено или отведено количество теплоты dQ, внешние и внутренние силы совершат работу dL, изменятся внутренняя энергия U и внешняя энергия Е. В связи с небольшой длиной межлопаточных каналов турбомашин пренебрегаем изменением потенциальной энергии газа, тогда изменение внешней энергий будет равно изменению кинетической энергии рабочего тела.

По закону сохранения энергии сумма изменений внутренней и внешней энергий газа за время dτ должна быть равна сумме подведенного иди отведенного количества теплоты и совершенной работы:

(dU + dE) dτ = dQ dτ + dL dτ, (2.9)

или для 1 кг рабочего тела:

(du + de) dτ = dq dτ + dl dτ . (2.10)

Общие количество теплоты, входящее в эти уравнения складывается из внешнего тепла q_внеш, которое может быть со знаком плюс или минус, и внутреннего, эквивалентного работе сил трения

.

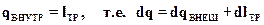Работа внешних и внутренних сил состоит из внешней работы 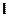внеш, отданной рабочим телом или подведенной к рабочему телу, работы сил трения l тр и работы гидродинамических сил в сечениях 0-0 и 1-1 (работы перемещения)

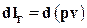
Следовательно, сумма работ всех сил составит

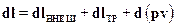(2.11)

Подставив (2.11) в (2.10) и предполагая, что процесс течения идет без трения 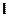тр= 0, и учитывая, что изменение кинетической энергии рабочего тела равно 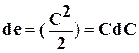, получил после сокращение на dτ

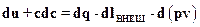(2.12)

Выражение (2.12) получено для турбины, когда работа отводится от газа и 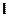имеет знак минус. Оно справедливо для течения без трения и с трением, хотя формально работа трения в выражении не входит. Последнее объясняется тем, что при наличии трения энергия газа уменьшается на величину dlтр и одновременно увеличивается на величину 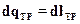, эквивалентную работе сил трения, так как работа трения переходит в теплоту и практически полностью идет на подогрев рабочего тела.

Учитывая, что du + d(pv) = di и проинтегрировав в пределах от сечения 0-0 до сечения 1-1, получим

(2.13)

Уравнение (2.12) и (2.13) можно применять для любого неподвижного канала (сопла, диффузора), для вращающейся решетки или колеса, для ступени турбомашин и для турбомашины в целом. При этом, параметры состояния и скорости газа во входном и выходном сечениях решетки, ступени или машины должны быть постоянными, или надлежащим образом осреднены.

В большинстве случаев процессы в турбомашинзх можно рассматривать как протекающие без теплообмена с окружающей средой, то есть адиабатные; при этом dq_внеш=0

Для неподвижного канала (dl_внеш = 0, ибо нет перемещения стенок канала. Тогда для изоэнтропийного (без трения) и адиабатного (с трением) процессов течения в неподвижных каналах из уравнения (2.13) получим, соответственно:

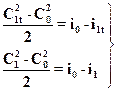(2.14)

Каждое из двух этих уравнений описывает три принципиально отличных процесса течения рабочего тела в неподвижном канале:

1. Процесс идет с ускорением (разгоном) потока С_1t > Со, i_1t < io (для действительного процесса С₁ > Со, i₁ < i₀). Газ расширяется в канале, его потенциальная энергия уменьшается, кинетическая - растет. Уравнение (2.14) показывает, что прирост кинетической энергии определяется уменьшением энтальпии рабочего тела.

2. Процесс идет с замедлением (торможением) рабочего тела С_1t<Сo, i_1t > i₀ (в действительном процессе C₁ < C₀, i₁ > io). Потенциальная энергия газа растет за счет его кинетической энергии, которая соответственно уменьшается. Такой процесс осуществляется в диффузоре.

3. Процесс дросселирования i_1t = io. При этом имеет место потеря работоспособности рабочего тела.