Понятие о законе обращения воздействия

Из уравнения непрерывности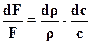

cкорость звука в сплошной среде определяется по выражению

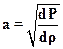, (2.38)

из этого выражения следует 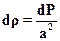. (2.39)

Согласно уравнению Бернулли для энергетически изолированного течения без трения можно записать

.

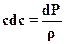Выразим из этого выражения dP, подставим его в уравнение (2.39) и полученное значение dρ/ρ подставим в уравнение неразрывности, в результате получим

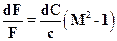. (2.40)

Форма потока в этой формуле определяется знаком dF.

Если требуется осуществить разгон (ускорение) потока, тогда dC>0.

В дозвуковой области М<1 и потому и dF<0, то есть площадь канала должна убывать в направлении течения. Если поток течет со сверхзвуковой скоростью, то М>1 и dF>0, то есть площадь канала должна возрастать. В точке потока, где скорость возрастая, достигает величины местной скорости звука, М=1 и потому dF=0.

Следовательно, для ускорения дозвукового потока требуются сопло сходящееся, разгон сверхзвукового потока возможен лишь в расходящемся сопле. Если дозвуковой поток должен быть разогнан до сверхзвуковой скорости, то сопло должно иметь сходяше-расходящуюся форму (сопло Лаваля). В самом узком месте сопла - горле осуществляется переход через скорость звука.

Если требуется затормозить поток, то dC<0 и форма потока и канала (диффузора) будет иметь обратный характер. При торможении дозвукового потока диффузор должен быть расходящейся формы. Торможение сверхзвукового требует канала сходящейся формы. Наконец, если сверхзвуковой поток потребуется замедлить так, чтобы скорость газа стала меньше звуковой, то диффузор должен иметь форму обращенного сопла Лаваля. В горле диффузора скорость, убывая, переходит через местное значение скорости звука с возникновением скачка.

Не меньший практический интерес представляет обратная задача, когда задана форма канала и как поведет себя дозвуковой или сверхзвуковой поток в этом канале? Ответ на этот вопрос можно получить анализируя уравнение (2.40).