Тема 41 Истечение газа под высоким давлением
41. 1 Основные теоретические сведения
Давление условно называется высоким, если при реализации соответствующей ему потенциальной энергии в энергию кинетическую плотность и температура газа, уменьшаясь, претерпевают существенные изменения.
В резервуаре или канале, из которого происходит истечение, давление, плотность, температура и скорость движения газа равны соответственно р1, r1, Т1, v1.
р, r, Т, v – те же самые параметры у выхода из отверстия (или на срезе сопла). Размеры сосуда настолько велики, что скорость газа внутри сосуда v1 » 0.
Скорость истечения газа равна:
v =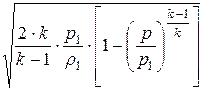 
, (41.1)
где k – показатель адиабаты.
Согласно уравнению состояния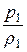 
= R × T1. Тогда скорость истечения может быть определена
v =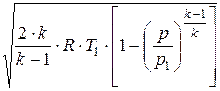 
.
Из формулы (41.1) следует, что с уменьшением давления вне сосуда, скорость истечения газа растёт, достигая максимального значения при истечении в вакуум (р = 0)
vmax =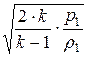 
. (41.2)
Скорость звука а – это скорость распространения упругих колебаний. Она связана с давлением и плотностью среды зависимостью а2 =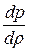 
.
Уравнение скорости истечения газа с учётом скорости распространения упругих колебаний запишется
v = а ×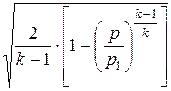 
. (41.1 а)
Максимальная скорость истечения при р = 0 будет равна
vmax = а ×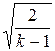 
. (41.2 а)
Поскольку скорость звука является конечной величиной, запишем уравнение энергии для двух сечений, в одном из которых скорость газа равна нулю, а во втором имеет конечное значение v:
+ 
= 
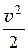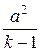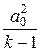. (41.3)
Отсюда следует, что максимально возможная, то есть предельная скорость газа достигается в том случае, если скорость звука в этом сечении равна нулю. Тогда
= 
, 
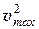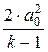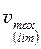= а0 × 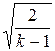. (41.4)
Из уравнения энергии определяем а2:
а2 =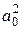 
- v2 × 
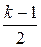. (41.3 а)
Отсюда следует, что с увеличение скорости движения газа v, скорость звука убывает. Следовательно, при достаточно большом перепаде давлений в сосуде и окружающей среде может быть достигнуто равенство скоростей потока и скорости звука в этом потоке.
Скорость потока, равная местной скорости звука, называется критической vкр, а соответствующая скорость звука акр.
Скорость движения потока по отношению к скорости распространения упругих колебаний (скорости звука) делится на дозвуковую (v < vкр) и сверхзвуковую (v > vкр). Вводится параметр, который характеризует область движения газа - число Маха М
М =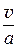 
. (41.5)
Это безразмерная скорость, которая показывает, во сколько раз скорость потока больше или меньше скорости звука. М > 1 – сверхзвуковая область движения газа, М < 1 – дозвуковая.
Критическая скорость движения газа при заданной температуре в резервуаре Т1 является постоянной величиной по ходу потока. Поэтому вводят в расчёт критерий скорости – приведенную скорость потока, которая является отношением скорости движения газа в данной точке к критической скорости
L =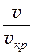 
= 
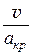. (41.6)
Приведенная скорость вдоль потока является постоянной в отличие от числа Маха.
Тема 42 Течение газа в конфузорах и диффузорах в одномерном приближении (движение газа в трубе переменного сечения)
Для анализа движения газа в каналах с переменным поперечным сечением воспользуемся уравнениями, выражающими закон сохранения массы и закон сохранения энергии. Закон сохранения массы представим в форме уравнения постоянства массового расхода вдоль потока:
Qm = r × v × w = const = C. (42.1)
Закон сохранения энергии используем в виде уравнения Бернулли для идеального газа в дифференциальной форме (пренебрегая величиной dz, то есть полагая dz = 0):
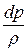+ v × dv = 0. (42.2)
Продифференцируем по x уравнение неразрывности (42.1):
= 
;
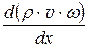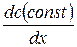r × v ×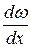 
+ r × w × 
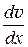+ v × w × 
= 0.
Разделив последнее уравнение на r ´ v ´ w получим:
× + 
× + 
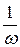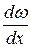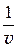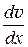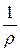× = 0.
Умножив полученное выражение на dx имеем:
+ 
+ 
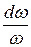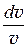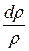= 0. (42.3)
Преобразуем первый член уравнения (42.2), использовав формулу скорости звука а2 = :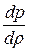
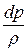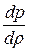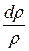= × = а2 × .
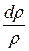Подставим полученное соотношение в уравнение (42.2):
а2 × 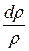+ v × dv = 0 или = - 
.
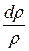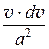Последнее равенство подставим в уравнение (42.3). Тогда
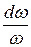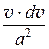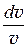- + = 0 или = - .
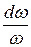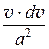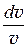В правой части уравнения вынесем за скобки 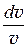. Получим
= 
× .
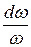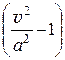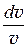Обозначим 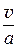= М – число Маха. Число Маха М – это безразмерная скорость, которая показывает, во сколько раз скорость потока v больше или меньше местной скорости звука а. Окончательно имеем уравнение Гюгонио:
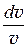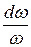× = . (42.4)
Следствия (анализ) уравнения Гюгонио
1. В дозвуковом потоке (v < а, М < 1) знак dv противоположен знаку dw. То есть при дозвуковом движении газа, так же, как и в случае несжимаемой жидкости, с возрастанием площади сечения трубы скорость движения уменьшается и наоборот.
Рисунок 72
2. В сверхзвуковом потоке (v > а, М > 1) знаки dv и dw одинаковы. Поэтому при уменьшении сечения м скорость движения снижается и наоборот.
Рисунок 73
Это объясняется тем, что произведение r × w из уравнения неразрывности r × v × w = const несмотря на увеличение w всё же уменьшается ввиду резкого уменьшения плотности газа r. И наоборот, произведение r × w увеличивается, несмотря на уменьшение w вследствие резкого увеличения плотности газа r. Если в дозвуковом потоке при изменении сечения трубы плотность газа изменяется незначительно по сравнению со скоростью, то при сверхзвуковом течении газа относительное изменение плотности превосходит по величине относительное изменение скорости. Возрастание скорости, таким образом, связано не только с изменением давления, но и с уменьшением плотности.
3. Если М = 1, то dw = 0 при w ¹ 0. Тогда соответствующее этому случаю сечение w будет критическим. Равенство dw = 0 означает наличие экстремума площади сечения. Причём этот экстремум означает минимальное сечение, так как при подходе к максимальному сечению дозвуковой поток замедляется и не может достигнуть М = 1, а сверхзвуковой ускоряется, что тоже не соответствует М = 1.
4. Если dw = 0 и сечение экстремально (максимальное или минимальное), то либо М = 1 и, следовательно, это сечение критическое, либо М ¹ 1, а dv =0, так как скорость принимает экстремальное значение. При дозвуковом потоке (М < 1) она максимальна в минимальном сечении и наоборот. В сверхзвуковом потоке (М > 1) она максимальна в максимальном сечении и минимальна в минимальном.
На основе анализа уравнения Гюгонио можно предложить способ получения сверхзвукового потока при истечении газа. К выходному сечению конфузорного насадка, в выходном сечении которого скорость газа равна скорости звука (М =1), присоединяют диффузорный насадок. В выходном сечении диффузора скорость газа может быть существенно больше скорости звука в этом сечении. По этому принципу рассчитывается сопло Лаваля.
Рисунок 74 – Сопло Лаваля
Дата добавления: 2015-08-26; просмотров: 4275;