Тема 35 Параметры, влияющие на коэффициенты сжатия, скорости и расхода при истечении жидкости из малого незатопленного отверстия в тонкой стенке при постоянном напоре

Для вычисления площади, скорости и расхода струи необходимо знать коэффициенты, характеризующие истечение: сжатия струи e, скорости j, и расхода m. Значения этих коэффициентов зависят от:

· формы и кромки отверстия;

· режима движения жидкости;

· поверхностного натяжения;

· положения отверстия относительно стенок резервуара.

Значение коэффициента сжатия e = 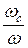для заданного отверстия зависит от степени сжатия струи.

Полное сжатие характеризуется тем, что струя вытекающей жидкости испытывает сжатие по всему периметру отверстия.

Неполное сжатие характеризуется тем, что струя подвергается сжатию только на некоторой части периметра.

Неполное сжатие может наблюдаться, например, когда отверстие в вертикальной или наклонной стенке резервуара примыкает непосредственно к дну (отсутствие сжатия по одной из сторон) или отверстие примыкает к дну и расположено в углу резервуара (отсутствует сжатие по двум сторонам) (рис. 59, а).

Рисунок 59 - Сжатие струи

В связи с этим при одинаковой площади отверстия и прочих равных условиях площадь сечения, сжатого на некоторой части периметра w_{с неп.}, больше, чем площадь сечения, сжатого по всему периметру w_{с пол.} (w_{с неп.} > w_{с пол.}). Отсюда получается, что при неполном сжатии коэффициент сжатия e_неп. больше, чем при полном сжатии e_пол. (e_неп. > e_пол.).

При полном сжатии различают совершенное и несовершенное сжатие.

Сжатие будет совершенным, если расстояния от любой грани отверстия до стенок и дна резервуара (сосуда) будут больше, чем утроенный соответствующий поперечный размер отверстия, то есть при l₁ > 3 b и l₂ > 3 S (рис. 59, б). Совершенное сжатие характеризуется наибольшей кривизной траекторий крайних струек вытекающей струи и соответственно, максимальным сжатием струи.

Несовершенное сжатие наблюдается, если расстояния от любой грани отверстия до стенок и дна резервуара (сосуда) будут меньше, чем утроенный соответствующий поперечный размер отверстия, то есть при l₁ < 3 b и l₂ < 3 S (рис. 59, в).

При несовершенном сжатии кривизна траекторий частиц вблизи отверстия меньше, чем при совершенном сжатии. В связи с этим сжатие по соответствующей стороне (близко расположенной к направляющей поток стенке или дну) уменьшается. Следовательно, площадь сжатого сечения при несовершенном сжатии w_{с нес.}, и при прочих равных условиях больше, чем при совершенном сжатии w_{с сов.} (w_{с нес.} > w_{с сов.}). Соответственно, коэффициент сжатия при несовершенном сжатии e_нес. больше, чем при совершенном сжатии e_сов. (e_нес. > e_сов.).

Неполнота и несовершенство сжатия приводят к увеличению коэффициента сжатия.

При неполном сжатии коэффициент расхода m_неп. больше, чем при полном сжатии m_пол.. При полном, но несовершенном сжатии коэффициент расхода m_нес. больше, чем при коэффициент расхода при совершенном сжатииm_сов.:

m_неп. > m_пол.;

m_нес. > m_сов..

В условиях совершенного сжатия процесс истечения происходит под действием сил тяжести, вязкости и поверхностного натяжения, которые определяются соответственно для круглого отверстия диаметром d:

числом Фруда Fr = ;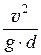

числом Рейнольдса Re = ;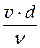

числом Вебера We= .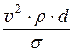

Коэффициенты расхода m при истечении через незатопленные круглые малые отверстия практически не зависят от влияния сил тяжести и поверхностного натяжения ( то есть наступает область, практически автомодельная относительно чисел Фруда и Вебера) при соблюдении условий

Fr = 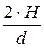> 10, то есть при 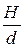> 5 и We = 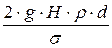> 2500.

Зависимости коэффициентов сжатия струи e, скорости j, и расхода m при совершенном сжатии от числа Рейнольдса представлены на рис. 60. Как видно, с увеличением Рейнольдса до 1×10⁵ коэффициент скорости j растёт, при дальнейшем увеличении Re значения j могут считаться постоянными и равными 0,97 (j_ос = 0,97).

Коэффициент сжатия струи e с ростом Re уменьшается, а при Re > 1×10⁵ коэффициент e также может считаться постоянным и приниматься равным 0,61…0,64.

Рисунок 60 – Зависимости коэффициентов сжатия струи e, скорости j, и расхода m при совершенном сжатии от числа Рейнольдса Re =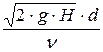

Зависимость коэффициента расхода m от Re достаточно сложная. Вначале при небольших значениях Re коэффициент m растёт, достигая максимума в пределах Re = 500…1000, а затем уменьшается. При Re > 3×10⁵ m перестаёт зависеть от числа Рейнольдса (наступает автомодельная область истечения относительно Re). В этих условиях m = 0,6…0,62.