Путем интегрирования уравнения изогнутой оси балки

В этом случае неизвестными функциями, определяющими положение точек поперечных сечений балки, являются z(x) и j (x) = a (x) (рис. 7.1). Совокупность значений этих параметров по длине балки образуют две функции от координаты х - функцию перемещений z(х) и функцию углов поворота j (х). Из геометрических построений (рис. 7.1) наглядно видно, что угол наклона касательной к оси х и угол поворота поперечных сечений при произвольном х равны между собой. В силу малости углов поворота можно записать

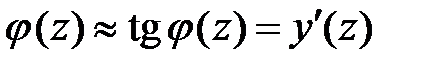. (7.1)

Из курса математического анализа известно, что кривизна плоской кривой z(х) выражается следующей формулой:

.

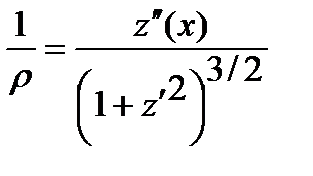Однако в связи с малостью величины 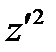по сравнению с единицей последнее выражение можно существенно упростить, и тогда

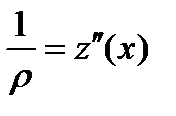. (7.2)

Учитывая выражение, полученное в предыдущей лекции, 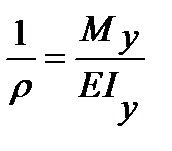, из (7.2) получим следующее важное дифференциальное соотношение:

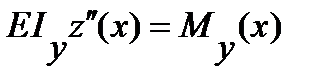, (7.3)

где I_у - момент инерции поперечного сечения балки относительно ее нейтральной оси; Е - модуль упругости материала; E I_у - изгибная жесткость балки.

Уравнение (7.3), строго говоря, справедливо для случая чистого изгиба балки, т.е. когда изгибающий момент M_у (х) имеет постоянное значение, а поперечная сила равна нулю. Однако это уравнение используется и в случае поперечного изгиба, что равносильно пренебрежению искривлениями поперечных сечений за счет сдвигов на основании гипотезы плоских сечений.

Введем еще одно упрощение, связанное с углом поворота поперечного сечения. Если изогнутая ось балки является достаточно пологой кривой, то углы поворота сечений с высокой степенью точности можно принимать равными первой производной от прогибов. Отсюда следует, что прогиб балки принимает экстремальные значения в тех сечениях, где поворот равен нулю.

В общем случае, для того чтобы найти функции прогибов z(х) и углов поворота j (х), необходимо решить уравнение (7.3) с учетом граничных условий между смежными участками.

Для балки, имеющей несколько участков, определение формы упругой линии является достаточно сложной задачей. Уравнение (7.3), записанное для каждого участка, после интегрирования содержит две произвольные постоянные.

На границах соседних участков прогибы и углы поворота являются непрерывными функциями. Данное обстоятельство позволяет определить необходимое число граничных условий для вычисления произвольных постоянных интегрирования.

Если балка имеет n - конечное число участков, из 2n числа граничных условий получим 2n алгебраических уравнений относительно 2n постоянных интегрирования.

Если момент и жесткость являются непрерывными по всей длине балки функциями M_у (х) и E I_у (х), то решение может быть получено как результат последовательного интегрирования уравнения (7.3) по всей длине балки:

интегрируя один раз, получаем закон изменения углов поворота:

,

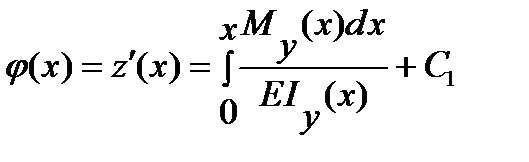интегрируя еще раз, получаем функцию прогибов:

.

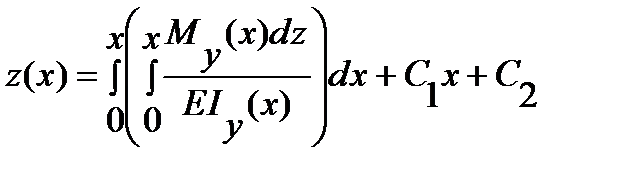Здесь C₁ и С₂ – произвольные постоянные интегрирования – должны быть определены из граничных условий.

Если балка имеет постоянное поперечное сечение по длине, то для определения функций прогибов и углов поворота удобно применить метод начальных параметров.