При прямом изгибе

В предыдущей лекции были рассмотрены вопросы, относящиеся к расчету балок на прочность. Однако в большинстве случаев практического расчета деталей, работающих на изгиб, необходимо также производить расчет их на жесткость.

Под расчетом на жесткость понимается оценка упругой податливости балки под действием нагрузок и подбор таких размеров поперечного сечения, при которых перемещения не будут превышать допускаемых величин. Для выполнения таких расчетов необходимо научиться вычислять перемещения попереч- ных сечений балки под действием любой внешней нагрузки. Кроме того, перемещения приходится определять и при расчете статически неопределимых конструкций (балок, рам, арок и т.д.).

В основе теории деформации при изгибе лежит гипотеза плоских сечений. Учитываются деформации только от изгибающего момента, деформациями от поперечной силы пренебрегают как малыми.

С учетом принятых допущений рассмотрим деформацию балки при прямом изгибе. Под действием внешних нагрузок, расположенных в одной из главных плоскостей балки, наблюдается искривление ее оси в той же плоскости, происходит так называемый прямой изгиб. Поперечные сечения при этом поворачиваются и одновременно получают поступательные перемещения (рис. 7.1).

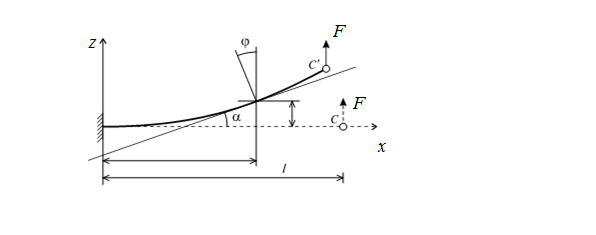
Рис. 7.1

Искривленная ось балки называется упругой линией.

Перемещение центра тяжести сечения по направлению, перпендикулярному к недеформированной оси балки, называется прогибом балки в данном сечении и обозначается z.

Прогибы и углы поворотов в балках являются функциями координаты x и их определение необходимо для расчета жесткости. Рассмотрим изгиб стержня в одной из главных плоскостей, например в плоскости xz. Как показывает практика, в составе реальных сооружений стержни испытывают весьма малые искривления (z_max/l = 10^-2 …10^-3, где z_max – максимальный прогиб; l – пролет балки).