Напряжения при чистом изгибе
Рассмотрим наиболее простой случай изгиба, называемый чистым изгибом. Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а поперечные силы равны нулю. Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сечений относительно друг друга.
Определим нормальные напряжения, возникающие при чистом изгибе балки, находящейся под действием моментов Му. В произвольной точке балки (рис. 6.5, т. А) в общем случае могут возникать нормальные напряжения как вдоль продольной оси σх, так и вдоль поперечных осей σy, σz.
| a |
| в |
| c |
| d |
| f |
| e |
| z |
| r |
| a¢ |
| в¢ |
| c¢ |
| d¢ |
| e¢ |
| f |
| в¢¢ |
| dj |
| dj |
| Рис. 6.5 |
| s |
| t |
| My |
| My |
| sэкв |
| A |
| B |
| sx |
| sz=0 |
| sy=0 |
| sx |
| t |
Однако экспериментально установлено, что нормальные напряжения σy, σz пренебрежимо малы по сравнению с напряжениями σx. Принимается так называемая гипотеза ненадавливания продольных волокон σy = 0, σz = 0. Поэтому можно принять, что материал балки находится при линейном напряженном состоянии вдоль оси x, и деформации подчиняются закону Гука. То есть нормальные напряжения при изгибе можно определить из формулы 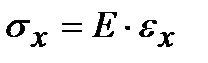 . Установим закон изменения деформаций при изгибе балки. Экспериментально получено, что в деформируемой балке поперечные сечения плоские до деформации остаются плоскими и поперечными после деформации, имеет место гипотеза плоских сечений. При этом верхние волокна удлиняются, нижние – укорачиваются, а продольная линия не меняет своей длины. Слой балки, не испытывающий при изгибе ни растяжения, ни сжатия, называется нейтральным слоем. Линия пересечения нейтрального слоя и плоскости поперечного сечения называется нейтральной линией.
. Установим закон изменения деформаций при изгибе балки. Экспериментально получено, что в деформируемой балке поперечные сечения плоские до деформации остаются плоскими и поперечными после деформации, имеет место гипотеза плоских сечений. При этом верхние волокна удлиняются, нижние – укорачиваются, а продольная линия не меняет своей длины. Слой балки, не испытывающий при изгибе ни растяжения, ни сжатия, называется нейтральным слоем. Линия пересечения нейтрального слоя и плоскости поперечного сечения называется нейтральной линией.
Определим относительную деформацию волокна ав εx (далее будем обозначать ее просто ε).
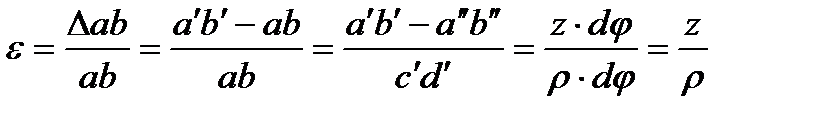 ,
,
где r – радиус кривизны нейтрального слоя,
z – расстояние от нейтрального слоя до рассматриваемого волокна балки.
Подставляя это соотношение в закон Гука, получим:
| e |
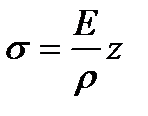 , (6.3)
, (6.3)
т.е. напряжения s линейно зависят от координаты z.
Используя интегральную связь между напряжениями и изгибающим моментом
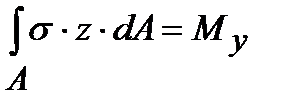 ,
,
подставляя в него соотношение (6.3), получим
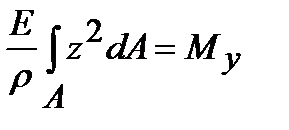 ,
,
где 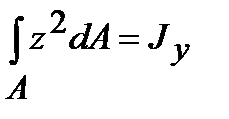 – осевой момент инерции сечения.
– осевой момент инерции сечения.
Подставляя полученное выражение в (6.3), имеем формулу для нормальных напряжений при изгибе
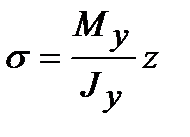 . (6.4)
. (6.4)
Эпюра нормальных напряжений показана на рис. 6.5. Как видно, на нейтральной линии они равны нулю, максимального значения напряжения достигают в крайних верхних и нижних волокнах балки:
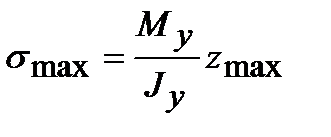 .
.
Обозначая 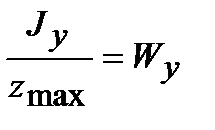 , получим формулу для максимальных напряжений в произвольном сечении
, получим формулу для максимальных напряжений в произвольном сечении
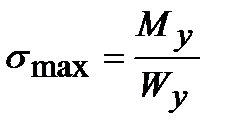 ,
,
где Wу – осевой момент сопротивления сечения изгибу, геометрическая характеристика поперечного сечения.
Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, т.е. в опасном сечении
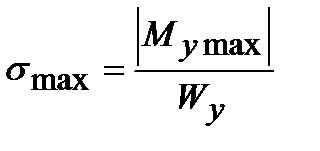 .
.
Условие прочности при изгибе формулируется следующим образом: балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений
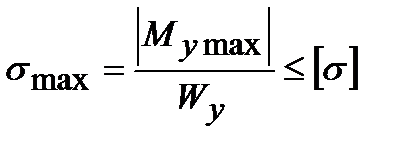 .
.
Величина допускаемых напряжений назначается в зависимости от материала, из которого изготовлена балка.
Пластичные материалы обладают примерно равными пределами текучести на сжатие sтс и на растяжение sтр , равны между собой и поэтому [sc]=[sp]=[s].
Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение и сжатие, как правило, не равны между собой [sc]³[sp] и поэтому необходимо записывать два условия прочности
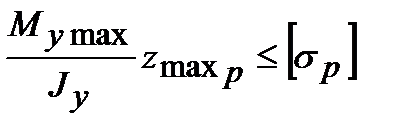 ,
, 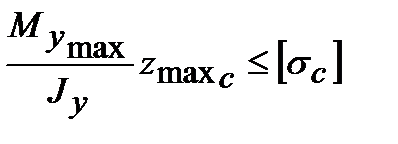 ,
,
где ymax p и ymax c – расстояния от нейтральной оси до наиболее удаленных растянутого и сжатого волокон.
Дата добавления: 2015-08-21; просмотров: 1858;
