И изгибающего момента
Если силы, действующие на стержень, перпендикулярны его оси, то стержень изгибается, или, говорят, работает на изгиб. Прямолинейный стержень, работающий на изгиб, называют балкой. Поперечное сечение балки может иметь любую форму, и для него, как известно, всегда можно построить пару взаимно перпендикулярных главных центральных осей инерции.
Наибольший практический интерес представляет случай, когда все внешние силы лежат в одной и той же плоскости, проходящей через одну из главных центральных осей инерции сечения. Возникающий при этом изгиб называют прямым плоским поперечным изгибом, а чаще просто изгибом. При этом изогнутая ось балки, называемая упругой линией, остается плоской кривой, лежащей в плоскости действия сил.
При изгибе одни продольные волокна балки растягиваются, другие – сжимаются, а между ними есть слой волокон, которые не растянуты и не сжаты. Этот слой называют нейтральным, а линию пересечения нейтрального слоя балки с ее поперечным сечением – нейтральной линией, или нейтральной осью.
Нейтральная ось (н.о.) совпадает с той главной центральной осью инерции сечения, которая перпендикулярна плоскости действия сил (ПДС), как показано на рис. 6.1.
Рис. 6.1
В поперечных сечениях балки в общем случае возникают два внутренних силовых фактора - поперечная сила Q и изгибающий момент М, которые определяются из условий равновесия отсеченной (любой) части балки.
Поперечная сила Qz в произвольном сечении балки равна алгебраической сумме всех внешних сил, приложенных к отсеченной части балки,
т. е. действующих на балку по одну сторону от данного сечения:
отсеч. (6.1)
Определяя поперечную силу в данном сечении, внешние силы, лежащие слева от сечения, берем со знаком плюс, если они направлены вверх, и со знаком минус, если - вниз. Для правой отсеченной части балки поступаем наоборот: внешние силы, лежащие справа от сечения, берем со знаком плюс, если они направлены вниз, и со знаком минус, если - вверх (рис. 6.2).
Рис. 6.2 Рис. 6.3
Это же правило можно сформулировать иначе: в выражении (6.1) внешние силы берутся со знаком плюс, если они стремятся повернуть рассматриваемую часть балки по часовой стрелке. Полученная при этом поперечная сила Q считается положительной.
Изгибающий момент Myв произвольном сечении балки равен алгебраической сумме моментов, взятых относительно центра тяжести сечения, всех внешних сил, приложенных к отсеченной части балки:
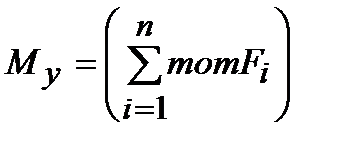отсеч. (6.2)
Определяя изгибающий момент в данном сечении, берем со знаком плюс те внешние моменты, которые вращают относительно центра тяжести сечения левую отсеченную часть балки по ходу часовой стрелки, а правую – против хода часовой стрелки. Полученный при этом изгибающий момент М считается положительным. Это правило иллюстрируется условным рисунком (рис. 6.3): изгибающий момент положителен, если внешние моменты изгибают ось балки выпуклостью вниз, сжимая верхние волокна балки. При этом следует мысленно защемить отсеченную часть балки в рассматриваемом сечении и разрешить ей изогнуться под действием приложенной к ней внешней силы.
При построении эпюр Q условимся положительные ординаты откладывать вверх от оси абсцисс, которая параллельна оси балки, а при построении эпюр М – вниз от оси абсцисс. При этом принятое правило знаков для изгибающего момента соответствует тому, что ординаты на эпюре М откладываются в сторону растянутого волокна. Знак на эпюре моментов можно не ставить. На эпюре Q знак ставится.
По эпюре изгибающих моментов определяется положение опасного сечения. Для балки с постоянным поперечным сечением опасным является то сечение, в котором возникает наибольший изгибающий момент Мmax .
Изгиб, при котором в поперечных сечениях балки возникает только изгибающий момент, называется чистым изгибом.
Построение эпюр поперечных сил и изгибающих моментов производится в следующей последовательности:
1. Определяются опорные реакции (при расчете консольных балок этого можно не делать).
2. Определяется количество участков, подлежащих расчету (границами участков являются места приложения сосредоточенных сил и моментов, места
начала и конца действия распределенных нагрузок.
3. По участкам, используя метод сечений, составляются выражения для определения поперечных сил и изгибающих моментов.
4. В полученные выражения подставляются координаты характерных точек и определяются числовые значения поперечных сил и изгибающих моментов в этих точках.
5. По полученным числовым значениям строятся эпюры внутренних усилий и определяются опасные сечения.
Пример 6.1. Для заданной балки (рис. 6.4 а) построить эпюры Q и М, указать опасное сечение. Дано: а = 3 м, b = 2 м, с = 1 м, d = 4 м, F = 120 кН, М1 = 20 кНм, М2 = 120 кНм, М3 = 20 кНм, q1 = 20 кН/м, q2 = 40 кН/м.
Решение
1. Определение опорных реакций.
Отбрасываем шарнирные опоры А и В, заменяя их действие силами
реакций RA и RB (рис. 6.4 б).
| М |
| а |
| б |
| в |
| г |
| г) |
Рис. 6.4
Балка находится в равновесии под действием плоской системы параллельных сил, следовательно, можно записать два уравнения статики:
.
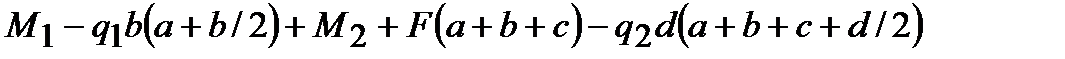
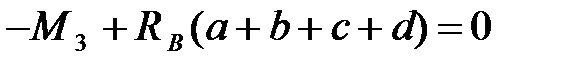Подставляя заданные числовые значения, определяем реакцию RB:
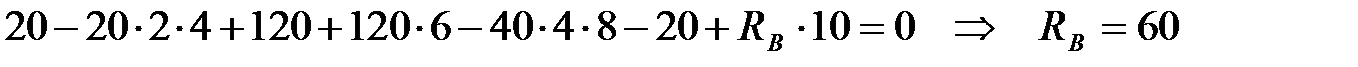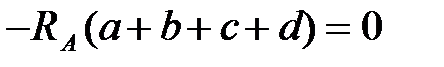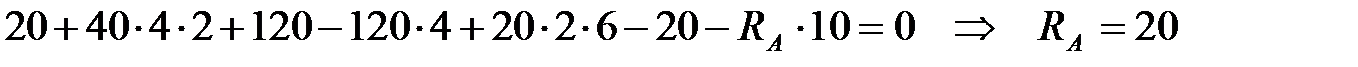кН;
.
кН.
Попутно отметим, что при отыскании опорных реакций правило знаков не играет существенной роли: составляя уравнение равновесия, можно
считать положительным любое направление момента, но при этом противоположное направление следует считать отрицательным.
Для проверки правильности найденных реакций составим дополнительное уравнение статики, например, сумму проекций сил на ось z.
.
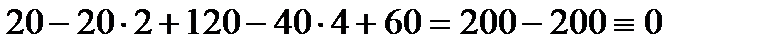Полученное тождество подтверждает правильность найденных значений
RA и RВ .
2. Построение эпюры Q.
Балка имеет четыре расчетных участка (пронумерованы римскими
цифрами).
I участок: 0 £ x £ а (отсчет сечений слева).
Q(x) = RA =20 кН = const..
II участок:а £ x £ а+b,
Q(x) = RA - q1(x - а) ;
при x = а Q = RA ;
при x = а+b Q = RA - q1 b =20 - 20×2 =- 20 кН.
На данном участке поперечная сила изменяется по линейному закону.
III участок: d £ x £ d+c (отсчет сечений справа).
Произвольное сечение находится на расстоянии x от правого конца балки. Согласно формуле (6.1) и рис. 6.2, получим:
Q(x) = -RB + q2 d- F = - 60 + 40×4 - 120 =- 20 кН = const.
IV участок: 0 £ x £ d,
Q(x) = -RB + q2 x ;
при x = 0 Q = -RB =- 60 кН;
при x = d Q = -RB + q2 d =- 60 + 40×4 =100 кН.
Поперечная сила меняется по линейному закону.
По полученным данным строим эпюру поперечных сил (рис. 6.4 в).
Обратим внимание на следующие особенности вида эпюры Q:
а) на тех участках балки, где нет распределенных нагрузок, поперечная сила постоянна и эпюра имеет вид прямой, параллельной оси балки;
б) на участках с равномерно распределенной нагрузкой эпюра Q имеет вид наклонной прямой, так как поперечная сила меняется по линейному закону;
в) в точке приложения сосредоточенной силы F на эпюре Q происходит скачкообразное изменение ординаты на величину приложенной силы. Направление скачка соответствует направлению силы (снизу вверх), если перемещаться по эпюре слева направо;
г) направление отсчета сечений на любом участке можно задавать произвольно, от любого конца балки - правого или левого. На виде эпюры это не отразится. Однако для упрощения вычислений рекомендуется рассматривать ту отсеченную часть балки, к которой приложена более простая нагрузка.
3. Построение эпюры М.
I участок: 0 £ x £ а ,
М(x) = - М1 + RA x ;
при x = 0 М = - М1 = - 20 кНм;
при x = а М = - М1 + RA а = - 20 + 20×3 = 40 кНм.
Изгибающий момент меняется по линейному закону, эпюра М на
данном участке представляет собой прямую наклонную линию.
II участок: а £ x £ а+b,
;
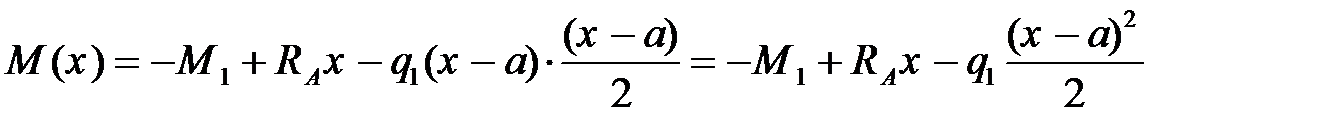при x = а М = - М1 + RA а = - 20 + 20×3 = 40 кНм;
при x = а+b М = - М1 + RA(а+b) - q1 b2/2= - 20 + 20×5 - 20×22/2 = 40 кНм.
Изгибающий момент меняется по квадратичному закону, эпюра представляет собой параболу. Точка, в которой поперечная сила Q обращается в нуль, является точкой экстремума изгибающего момента М, поэтому необходимо найти ее координату x0 и вычислить значение Мmax. Приравнивая нулю
выражение Q(x) на этом участке, получим:
Q(x) = RA - q1(x - а) = 0,
откуда x0 = RA/ q1 + а = 1 + 3 = 4 м,
Mmax = M(x0) = - M1 + RA x0 - q1(x0 - а)2/2 = - 20 + 20×4 - 20(4 - 3)2/2 = 50 кНм.
III участок: d £ x £ d+c,
;
при x = d М = - М3 + RB d - q2 d2/2= - 20 + 60×4 - 40×42/2 = - 100 кНм;
при x = d+c М = - М3 + RB (d + c) - q2 d(d/2+ c)+F c = - 20 + 60×5 -
- 40×4(2 + 1) + 120×1 = - 80 кНм.
Изгибающий момент меняется по линейному закону, эпюра имеет вид
прямой наклонной линии.
IV участок: 0 £ x £ d,
;
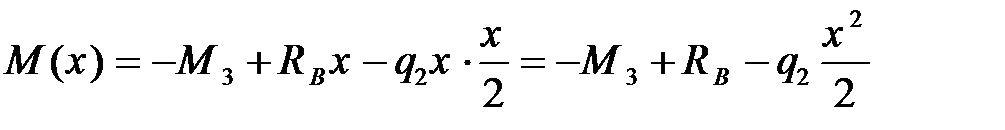при x = 0 М = - М3 = - 20 кНм;
при x = d М = - М3 + RB d - q2 d2/2 = - 20 + 60×4 - 40×42/2 = - 100 кНм.
Найдем координату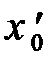 
точки, в которой Q(x) = 0 :
Q(x) = - RB + q2 x = 0, откуда 
= RB / q2 = 60/40 = 1,5 м.
M( ) = - M3 + RB - q2 2/2 = - 20 + 60×1,5 - 40×1,52/2 = 25 кНм.
По трем полученным значениям строим эпюру М. Она имеет вид параболы с вершиной в точке .
Анализируя эпюру М (см. рис. 6.4 г), определяем опасное сечение балки: Мmax = 100 кНм в точке приложения сосредоточенной силы F.
Построение эпюр поперечной силы Qz и изгибающего момента My является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Qz и My определяется опасное сечение, т.е. сечение, в котором может произойти разрушение.
Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения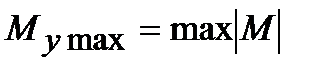 
.
В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила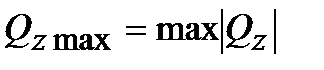 
. В данном случае опасным является место закрепления балки.
Контроль правильности построения эпюр можно осуществить по следующим правилам:
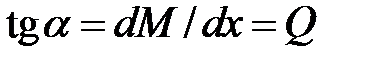а) на тех участках, где нет распределенных нагрузок (q = 0), на эпюре Q – прямая, параллельная оси абсцисс, т. е. Q = const. На эпюре М на таких участках также прямая, но имеющая наклон под углом a к оси эпюры, причем
;
б) в точках приложения сосредоточенных сил на эпюре М имеем изломы, направленные навстречу силам;
в) в месте приложения пары сил на эпюре Q никаких изменений не наблюдается, на эпюре М имеется скачок на величину момента данной пары;
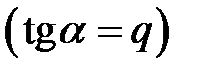г) на участках с равномерно распределенной нагрузкой (q = const) эпюра Q представляет собой прямую, наклоненную к оси балки под углом a . Эпюра М - квадратная парабола, выпуклость которой направлена по нагрузке;
д) при движении по эпюре слева направо на тех участках, где поперечная сила Q > 0, изгибающий момент М возрастает. На участках, где Q < 0, М убывает. В той точке, где поперечная сила Q = 0, М имеет экстремум (минимум, если нагрузка q направлена вниз, или максимум, если наоборот);
е) в точке приложения сосредоточенной силы на эпюре Q должен быть скачок, равный по величине и знаку приложенной силе;
ж) чем больше по модулю величина Q , тем круче изменяется эпюра М;
з) на свободных концах балки изгибающий момент равен нулю.
Эти правила справедливы, если проверять эпюры, начиная с левого конца балки к правому.
Дата добавления: 2015-08-21; просмотров: 1241;