Напряжения в поперечном сечении
Опыты показывают, что если на поверхности бруса круглого сечения нанести прямоугольную сетку, а на торцевой поверхности нанести радиальные линии (рис. 5.4), то после деформации кручения окажется, что:
| B |
| B1 |
| B |
| B1 |
| j |
| g |
| Рис. 5.4 |
| r |
| dA |
| t |
| T |
| x |
| dx |
а)все образующие поворачиваются на один и тот же угол g, а прямоугольники, нанесенные на поверхности, превращаются в параллелограммы;
б) торцевые сечения остаются круглыми, плоскими, расстояния между ними не меняются;
в) каждое сечение поворачивается относительно другого на некоторыйугол j, называемый углом закручивания;
г) радиальные линии на торцевой поверхности остаются прямыми.
На основании этих наблюдений можно заключить, что может быть принята гипотеза Бернулли (гипотеза плоских сечений), а в вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, а нормальные напряжения равны нулю.
Рассмотрим поперечное сечение вала, расположенное на некотором расстоянии х от торцевого сечения, где Мк = T (рис. 5.4). На элементарной площадке dА будет действовать элементарная сила t×dА, момент относительно оси вала, создаваемый этой силой равен (t×dА)×r. Крутящий момент Мк, в сечении равен
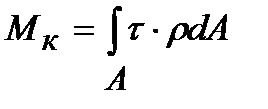 . (5.1)
. (5.1)
Для того чтобы проинтегрировать это выражение, необходимо знать закон распределения напряжений в сечении. Выделим из вала элементарное кольцо длиной dх и толщиной dr (рис. 5.5).
Правый торец элемента повернется относительно левого на угол dj, образующая СВ повернется на угол g и займет положение СВ1. Угол g – относительный сдвиг. С одной стороны, из треугольника ОВВ1 найдем:
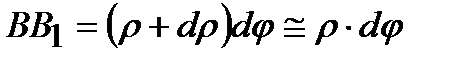 .
.
| C |
| r |
| dr |
| B |
| B1 |
| O |
| dj |
| g |
| dx |
| Рис. 5.5 |
| tmax |
С другой стороны, из треугольника СВВ1 получим: 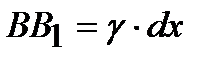 .
.
Приравнивая правые части полученных выражений, имеем: 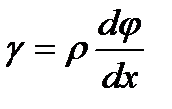 .
.
На основании закона Гука при сдвиге:
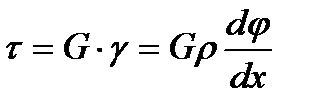 . (5.2)
. (5.2)
Подставив выражение (5.2) в (5.1), получим:
 .
.
Откуда
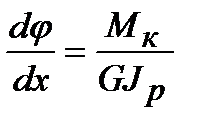 . (5.3)
. (5.3)
Подставим значение 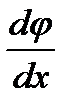 в выражение (5.2) и получим:
в выражение (5.2) и получим:
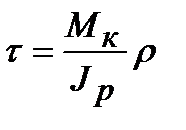 . (5.4)
. (5.4)
Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки и одинаковы в точках, одинаково удаленных от центра тяжести сечения (рис. 5.5). При r = 0 получим t = 0.
Наибольшие напряжения возникают в точках контура сечения при r = R:
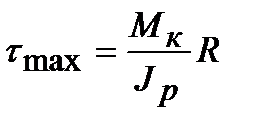 .
.
Величина отношения полярного момента инерции к радиусу вала называется моментом сопротивления сечения при кручении, или полярным моментом сопротивления  .
.
Для сплошного круглого сечения 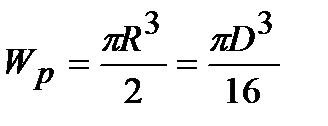 .
.
Для кольцевого сечения 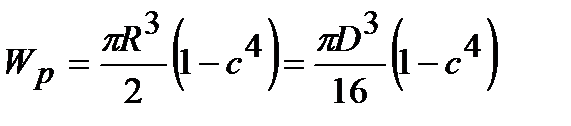 , где
, где 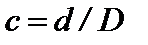 .
.
Тогда максимальные касательные напряжения равны
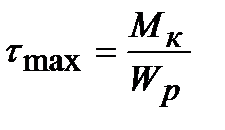 . (5.5)
. (5.5)
Дата добавления: 2015-08-21; просмотров: 1108;
