Прямоугольник
Определим момент инерции сечения относительно оси y0, проходящей через центр тяжести прямоугольника высотой h и шириной b параллельно основанию (рис. 4.5). Выделим из прямоугольника линиями, параллельными оси y, элементарную полоску высотой dz и шириной b. Площадь этой полоски dA=b×dz, расстояние от полоски до оси y равно z. Подставим эти величины в выражение момента инерции относительно оси y (4.6):
|
| y |
| z |
| z |
| dz |
| h |
| b |
| C |
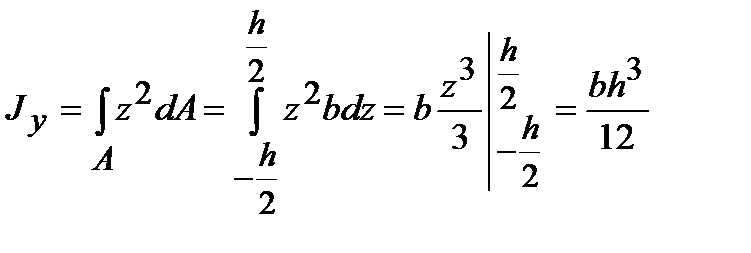 .
.
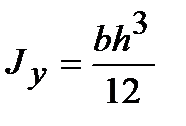 . (4.18)
. (4.18)
Аналогично, получим:
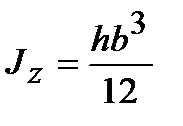 . (4.19)
. (4.19)
Очевидно, что 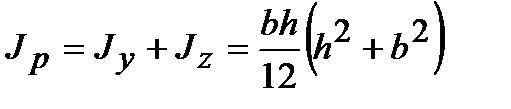 ,
, 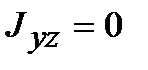 .
.
Дата добавления: 2015-08-21; просмотров: 729;
