При повороте осей
Найдем зависимость между моментами инерции относительно осей y, z и моментами инерции относительно осей y1, z1, повернутых на угол a. Пусть Jy > Jz и положительный угол a отсчитывается от оси y против часовой стрелки. Пусть координаты точки М до поворота – y, z, после поворота – y1, z1 (рис. 4.4).
Из рисунка следует:
; 
.
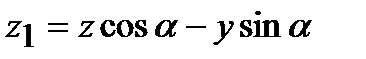Теперь определим моменты инерции относительно осей y1 и z1:
,
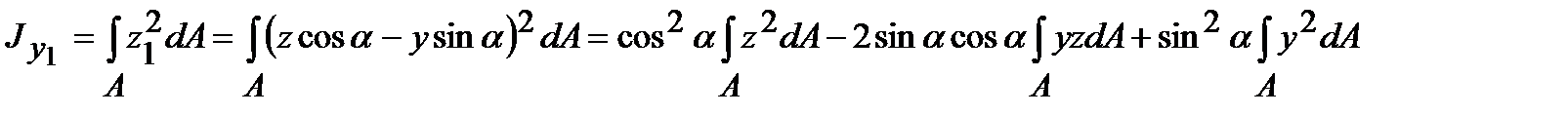или
|
| M |
| z |
| z1 |
| y1 |
| y |
| a |
| y |
| y1 |
| z1 |
| z |
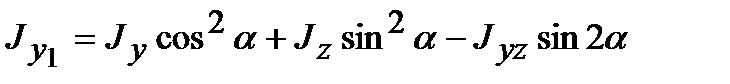. (4.13)
Аналогично:
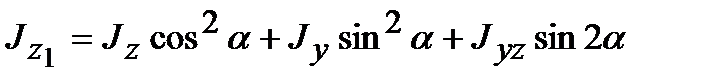. (4.14)
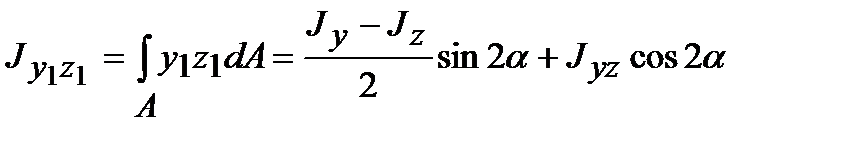(4.15)
Сложив почленно уравнения (4.13) и (4.14), получим:
,
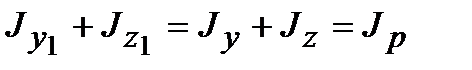т.е. сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат.
Дата добавления: 2015-08-21; просмотров: 701;