Моменты инерции сечений
К геометрическим характеристикам плоских сечений относятся также моменты инерции. Различают осевые, полярные и центробежные моменты сечений.
Осевым моментом инерции сечения называется взятая по всему сечению сумма произведений элементарных площадок на квадраты их расстояний до некоторой оси, лежащей в плоскости рассматриваемого сечения. Так, относительно осей у и z (рис. 4.1) осевые моменты инерции определяются интегралами вида:
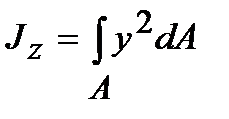 ;
; 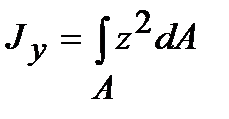 . (4.6)
. (4.6)
Величина осевого момента инерции служит характеристикой способности балки сопротивляться деформации изгиба.
Полярным моментом инерции сечения называется взятая по всему сечению сумма произведений элементарных площадок на квадраты их расстояний до некоторой точки О сечения (рис. 4.1):
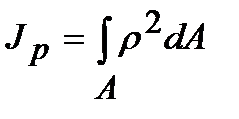 , (4.7)
, (4.7)
где r – расстояние от площадки dА до полюса.
Полярный момент инерции характеризует способность сечения сопротивляться деформации кручения.
Центробежным моментом инерции сечения относительно осей Оу и Оz называется взятая по всему сечению сумма произведений элементарных площадок на расстояния их до этих осей. Центробежный момент инерции сечения определяются интегралом
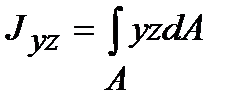 . (4.8)
. (4.8)
Если полярный момент инерции вычисляется относительно начала системы координат (рис. 4.1), то 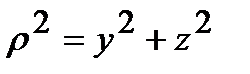 и
и
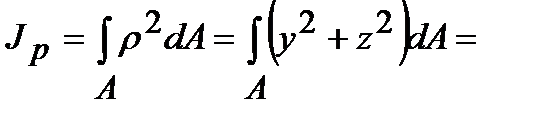
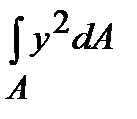 +
+ 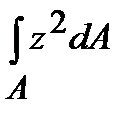 ,
,
следовательно,
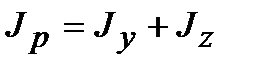 , (4.9)
, (4.9)
т.е. сумма осевых моментов инерции сечения относительно любых двух взаимно перпендикулярных осей, проходящих через данную точку, равна полярному моменту инерции этого сечения относительно этой точки.
|
| y1 |
| y2 |
| z1 |
| z2 |
| y |
| z |
| dA1 |
| dA2 |
Центробежный момент инерции сечения относительно осей, хотя бы одна из которых является осью симметрии, равен нулю. Действительно для симметричной фигуры всегда можно выделить два элемента ее площади (рис. 4.2), которые имеют одинаковые ординаты у1=у2=у, и равные по величине, но противоположные по знаку абсциссы z1=z и z2=–z. Тогда
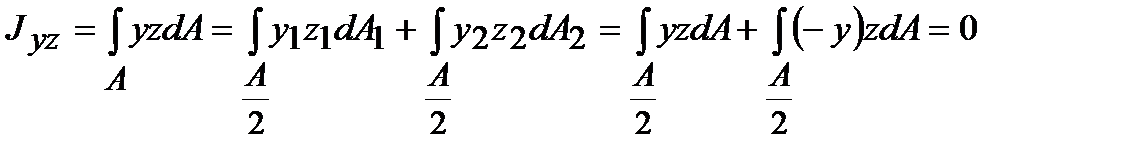 .
.
Дата добавления: 2015-08-21; просмотров: 942;
