Главные оси инерции и главные моменты инерции

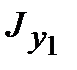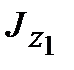С изменением угла поворота осей a каждая из величин и меняется, а сумма их остается неизменной. Следовательно, существует такое значение

a = a₀, при котором моменты инерции достигают экстремальных значений, т.е. один из них достигает своего максимального значения, а другой – минимального. Для нахождения значения a₀ возьмем первую производную от 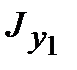(или 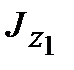) и приравняем ее нулю:

,

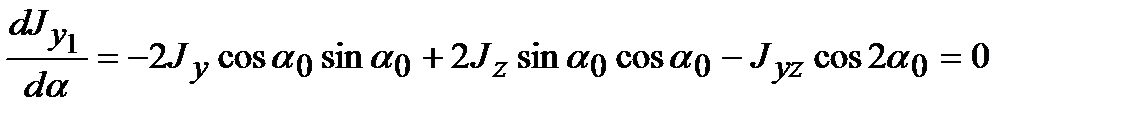или ,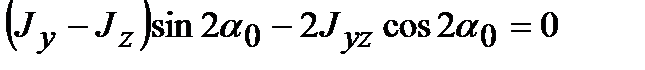

откуда

. (4.16)

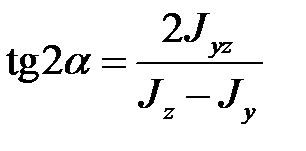Покажем, что относительно полученных осей центробежный момент инерции равен нулю. Для этого приравняем правую часть уравнения (4.15) нулю: 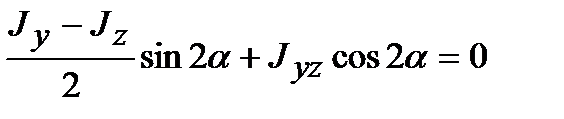, откуда , т.е. получили ту же формулу для a₀.

Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются главными осями. Если эти оси являются также и центральными, то они называются главными центральными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

Обозначим главные оси через y₀ и z₀. Тогда

;

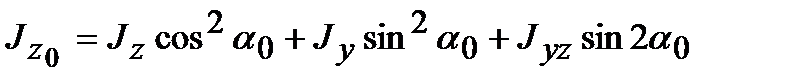; (4.17)

.

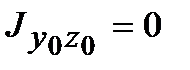Если сечение имеет ось симметрии, то эта ось всегда является одной из главных центральных осей инерции сечения.