Треугольник

Рис. 4.6

dz₁

z₁

y₁

z₁

b₁

Определим момент инерции треугольника относительно оси у₁, проходящей через основание (рис. 4.6)

Элементарная площадка .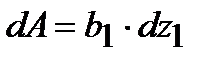

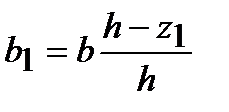Из подобия треугольников получаем:

где b – основание треугольника; h – его высота.

Таким образом,

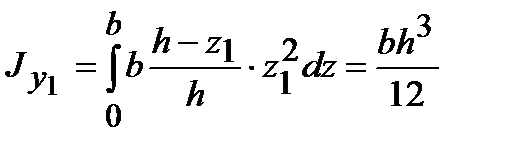Расстояние от основания треугольника до центра тяжести равно 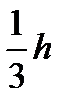, поэтому, используя правила переноса, находим момент инерции относительно центральной оси у, параллельной основанию

Круг

Определим сначала полярный момент инерции относительно центра круга (рис. 4.7). За dA примем площадь бесконечно тонкого кольца толщиной dr , расположенного на расстоянии r от центра круга dA = 2prdr.

Тогда

Рис. 4.7

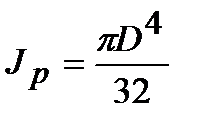(4.20)

Теперь определим осевые моменты инерции. Очевидно, что в силу симметрии ; но .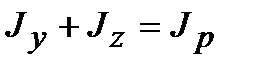

Откуда 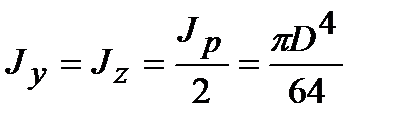. (4.21)

Кольцо

Рис. 4.8

Определим моменты инерции кольца, у которого R – наружный радиус, r – внутренний радиус (рис. 4.8). Интегрируя полученное ранее выражение для полярного момента инерции в пределах от r до R, получим

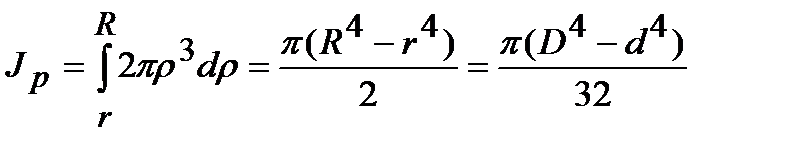Это выражение может быть представлено в виде

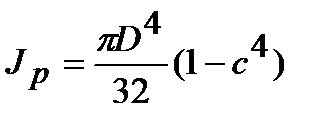, (4.22)

где .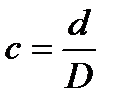

Соответственно

. (4.23)

Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:

, (4.24)

что непосредственно следует из свойств определенного интеграла.

Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.

Нашей промышленностью выпускаются стандартные прокатные профили (двутавр, швеллер, уголок равнобокий, уголок неравнобокий), которые могут быть использованы как готовые элементы конструкций (балки, стойки, элементы ферм и т.д.). Размеры прокатных профилей стандартизированы и сведены в таблицы сортаментов прокатной стали, которые приводятся в приложениях почти всех учебников и сборников задач по сопротивлению материалов. В этих таблицах приводятся все размеры сечений и основные геометрические характеристики прокатных профилей в соответствии с их номером.

Вопросы для самопроверки

1. По каким формулам определяют осевые, центробежный и полярный моменты инерции? Каковы их размерности?

2. Какие оси называют главными? Сколько главных осей может иметь плоская фигура?

3. Какие оси называют главными центральными? Сколько таких осей может иметь плоская фигура в общем случае?

4. Для каких фигур можно без вычислений установить положение главных центральных осей?

5. Какова зависимость между осевыми моментами инерции при параллельном переносе осей?

6. Какой из двух моментов инерции квадрата больше: относительно центральной оси, параллельной стороне квадрата, или относительно оси, совпадающей с диагональю?

7. Как определить момент инерции сложной фигуры, если ее можно разбить на простые части, для которых моменты инерции известны?

8. Какие моменты инерции всегда положительны?

<23 24 252627 28 29 >

Дата добавления: 2015-08-21; просмотров: 937;