Перемещения при плоском изгибе
При изгибе в качестве перемещений рассматриваются прогиб и угол поворота поперечного сечения. Прогибом балки δ называется величина, на которую перемещается центр тяжести поперечного сечения в направлении, перпендикулярном первоначальной оси балки. Углом поворота поперечного сечения q называется угол, на который поворачивается поперечное сечение при деформации балки (рис. 6.7).
В дальнейшем будем считать, что прогибы и углы поворота балки малы и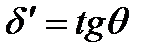 
, а 
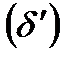<< 1. Приближенное дифференциальное уравнение изогнутой оси балки имеет вид: 
.
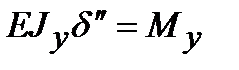| l |
| F |
| q |
| d |
| Рис. 6.7 |
, 
,
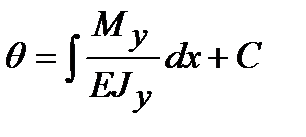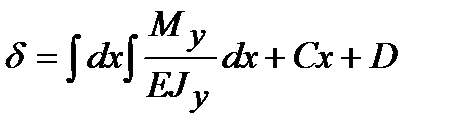где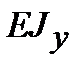 
– жесткость при изгибе;
С и D – константы интегрирования, которые представляют собой прогиб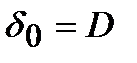 
и угол поворота 
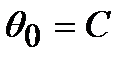в начале координат и определяются из граничных условий задачи.
В связи с неравномерным распределением напряжений по сечению балки рациональным можно считать сечение балки, которое при равной с другими сечениями площади имеет наименьшие напряжения.
Максимальные напряжения, возникающие в балке при действии заданной нагрузки, тем меньше
| z |
| z |
| y |
| y |
| h |
| b |
| h |
| b |
| a |
| б |
| Рис. 6.8 |
Поэтому сечения с большим Wу будут более рациональными. Так, например, прямо- угольное сечение, показанное на рис. 6.8 а предпочтительнее использовать при изгибе под действием вертикальной нагрузки, так как осевой момент сопротивления сечения изгибу для него будет больше, чем для этого же сечения, но повернутого на 90о (рис. 6.8 б).
Анализируя эпюры напряжений, можно отметить, что на продольной линии нормальные напряжения равны нулю, касательные напряжения достигают максимума, в крайних волокнах, наиболее удаленных от продольной линии, наоборот, нормальные напряжения достигают наибольших по модулю значений, а касательные напряжения равны нулю. Расчетная практика показала, что нормальные напряжения, как правило, в несколько раз больше касательных. Поэтому имеет смысл проектировать сечения так, чтобы в зоне действия больших напряжений находилась бы большая часть материала. Этому требованию отвечают сечения в виде двутавровых и швеллеровых прокатных профилей, а также различные коробчатые и кольцевые сечения (рис. 6.9).
| Рис. 6.9 |
Вопросы для самопроверки
1. Что называется балкой?
2. Какой вид нагружения называется изгибом?
3. Какой изгиб называется чистым, поперечным?
4. Как вычисляется изгибающий момент в поперечном сечении балки?
5. Как вычисляются поперечная и продольная силы в поперечном сечении балки?
6. Какие уравнения используются для определения значений опорных реакций?
7. Как проверить правильность определения опорных реакций?
8. Как формулируется гипотеза плоских сечений?
9. Что представляют собой нейтральный слой и нейтральная линия и как они расположены?
10. По какой формуле определяются нормальные напряжения в поперечном сечении балки при чистом изгибе и как они изменяются по высоте балки?
11. Что называется моментом сопротивления при изгибе и какова его размерность?
12. По какой формуле определяются нормальные напряжения в поперечных сечениях балки при поперечном изгибе?
13. Запишите формулу для определения касательных напряжений в поперечных сечениях балки при прямом поперечном изгибе.
14. Какой вид имеют эпюры касательных напряжений в поперечных сечениях прямоугольной и двутавровой формы?
15. Как находятся главные напряжения при изгибе?
16. Как направлены главные площадки на уровне нейтрального слоя и в точках, наиболее удаленных от этого слоя?
17. Что представляют собой траектории главных напряжений?
18. Какие формы поперечных сечений являются рациональными для балок из пластичных материалов?
Дата добавления: 2015-08-21; просмотров: 1023;