Внутренние силовые факторы при изгибе

Пример 1.Рассмотрим балку, на которую действует пара сил с моментом т и внешняя сила F (рис. 29.3а). Для определения вну­тренних силовых факторов пользуемся методом сечений.

Рассмотрим равновесие участка 1 (рис. 29.36).

Под действием внешней пары сил участок стремится развер­нуться по часовой стрелке. Силы упругости, возникающие в сече­нии 1, удерживают участок в равновесии.

Продольные силы упругости выше оси бруса направлены направо, а силы ниже оси направлены налево. Таким образом, при равновесии участка 1 получим: ΣF_Z = 0. Продоль-ная сила N в сечении равна нулю. Момент сил упругости относительно оси Ох может быть получен, если суммировать элементарные моменты сил упругости в

сечении 1- 1 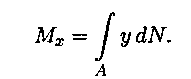относительно оси Ох:

Этот момент называют изгибающим моментом М_х — М_И.

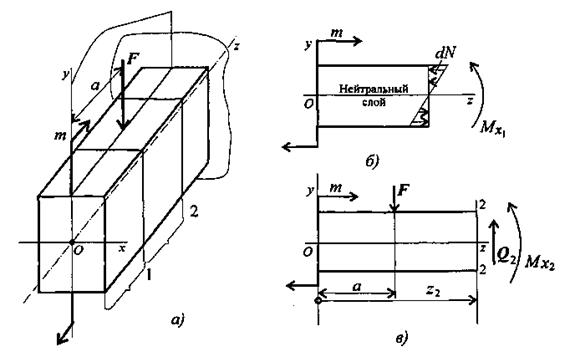Рис 29.3

Из схемы вала на рис. 29.3 б видно, что часть волокон (выше оси) испытывают сжатие, а волокна ниже оси растянуты. Следовательно, в сечении должен существовать слой не растянутый и не сжатый, где напряжения σ равны нулю.

Такой слой называют нейтральным слоем (НС). Линия пересе­чения нейтрального слоя с плоскостью поперечного сечения бруса называют нейтральной осью.

Нейтральный слой проходит через центр тяжести сечения. Здесь нейтральный слой совпадает с осью Ох.

Практически величина изгибающего момента в сечении опреде­ляется из уравнения равновесия:

Σ m _{x 1-1} = т — М_x1 = 0; М_x1 = т.

Таким образом, в сечении 1-1 продольная сила равна нулю, из­гибающий момент в сечении постоянен.

Изгиб, при котором в поперечном сечении бруса возникает толь­ко изгибающий момент, называется чистым изгибом.

Рассмотрим равновесие участка бруса от свободного конца до сечения 2 (рис. 29.Зв).

Запишем уравнения равновесия для участка бруса:

ΣF_y = 0; - F + Q₂ = 0; Q₂ = F = const.

В сечении бруса 2-2 действует поперечная сила, вызывающая сдвиг.

Σm_x2-2 = 0; т - F(z₂ - а) – М_x2 = 0.

Изгибающий момент в сечении: М_x2 = m - F(z₂ - a);

z₂ — расстояние от сечения 2 до начала координат.

Изгибающий момент зависит от расстояния сечения до начала координат.

Изгиб, при котором в поперечном сечении бруса возникает изги­бающий момент и поперечная сила, называется поперечным изгибом.