Дифференциальные зависимости при прямом поперечном изгибе

Построение эпюр поперечных сил и изгибающих моментов су­щественно упрощается при использовании дифференциальных зави­симостей между изгибающим моментом, поперечной силой и интен­сивностью равномерно распределенной нагрузки (теорема Журав-ского):

Поперечная сила равна производной от изгибающего момента по длине балки:

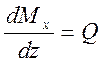
Интенсивность "равномерно распределенной нагрузки равна производной от поперечной силы по длине балки:

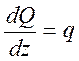
Из выше указанного следует:

если М_и = const, то Q = 0; если Q = const; то q = 0.

Лекция№ 30

Расчет прочности при деформации изгиба.

Кратко напомним, что при растяжении или сжатии возникает внутренний силовой фактор — продольная сила, при сдвиге — поперечная сила, а при кручении — крутящий момент в плоскости поперечного сечения.

Изгиб отличается от рассмотренных видов нагружения тем, что в этом случае появляются два внутренних силовых фактора: поперечная сила Q, как при сдвиге, и изгибающий момент М (рис. 101). Рассмотрим изгиб, при котором плоскость изгибающей нагрузки совпадает с одной из главных осей инерции по-

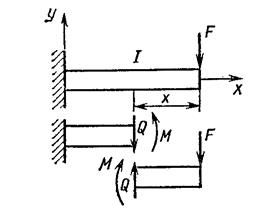
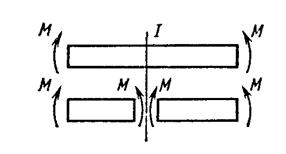
Рис. 101. Схема изгиба Рис. 102. Чистый изгиб бруса

перечного сечения. Такой изгиб иногда называется прямым, а чаще просто изгибом. Стержень, работающий на изгиб, называется балкой.

Частный вид изгиба, при котором поперечная сила равна нулю, называется чистым изгибом (рис. 102). В этом случае в поперечных сечениях балки возникает только изгибающий момент М. В отличие от него изгиб, при котором поперечная сила не равна нулю, называется поперечным изгибом (см. рис. 101).

Изгиб относится к простому виду нагружения, несмотря на то, что при изгибе балки возникают два внутренних силовых фактора Q и М.

Однако, как покажет дальнейшее рассмотрение изгиба, определяющим внутренним силовым фактором при изгибе является единственный внутренний силовой, фактор — изгибающий момент. Влиянием перерезывающей силы при изгибе балки можно пренебречь.

Внутренние силовые факторы при изгибе Q и М определяются методом сечений (см. рис. 101). Рассмотрим условия равновесия отсеченной части балки. Проекция всех сил на ось у равна нулю:

Q — F = 0; Q = F.

Момент относительно сечения I всех сил равен нулю

М + F_x = 0, М = — Fx.

Поперечная сила Q в сечении I равна действующей на отсеченную часть внешней силе F, а изгибающий момент М равен моменту внешней силы относительно рассматриваемого сечения.

Теперь рассмотрим действие нескольких внешних сил на балку (рис. 103). В дальнейшем будем изображать балку

в виде прямой линии — геометрического места центров тяжести поперечных сечений балки. Определим внутренние силовые факторы в произвольном

сечении I Для этого рассечем балку по сечению I , приложим в этом сечении неизвестные внутренние силовые факторы при изгибе Q и М и составим уравнение равновесия для отсеченной части балки:

Σ F_y = 0 , ΣМ = 0

Сумма всех сил на ось х тождественно равна нулю, поскольку продольные силы на балку не действуют. В дальнейшем рассматриваем только два приведенных уравнения равновесия, индекс «y» не указываем. Из первого уравнения следует

ΣF = -F_x + F₂ + Q_l = 0,

откуда определяем поперечную силу

Рис. 103 Определение сечении I

внутренних силовых Q₁= F₁ – F₂.