Методом сечения Полученное выражение можно обобщить

Поперечная сила в рассматриваемом сечении равна алгебраической сумме всех сил, действующих на балку до рассматриваемого сечения:

Q = ΣF_i

Поскольку речь идет об алгебраической сумме, в которой необходимо учитывать знак действующих сил, необходимо сформулировать правило знаков при определении значений поперечной силы в сечении; внешние силы активные и реактивные, лежащие по левую сторону от сечения, считаются положительными, если они направлены вверх, отрицательными — вниз, а по правую сторону — наоборот (рис. 104).

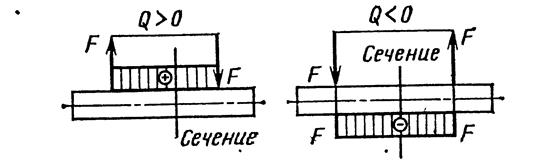
Рис. 104. Правила знаков поперечной силы Q

Перейдем к рассмотрению второго уравнения равновесия. Определим сумму моментов относительно рассматриваемого сечения I

(ΣМ)_I =M_I + F₁l₁ - F₂l₂ = 0

откуда

M_I = - F₁l₁ + F₂l₂

Это выражение также обобщим. Изгибающий момент в рассматриваемом сечении равен алгебраической сумме моментов относительно этого сечения всех внешних сил и моментов, действующих на балку до рассматриваемого сечения:

М = Σ M_i

Сформулируем пра вило знаков при определении зна-чения изгибающего момента: момент, изгибающий балку выпуклостью вниз, считается положительным, а вверх — отрицательным (рис. 105). Для лучшего запоминания Рис 105. Правило знаков изгибающего

правила знаков изгибающего момента М

момента следует отметить, что его значение откладывается в сторону сжатого волокна (см. рис. 105): при изгибе выпуклостью вниз сжатое волокно наверху балки, т. е. в плюс, а при изгибе выпуклостью вверх, сжатое волокно внизу — момент откладывается вниз — минус.

Напомним, что существует три вида опор балок:

1) шарнирно-подвижная опора (рис. 106);

2) шарнирно-неподвижная опора (рис. 107);

3) жесткая заделка или защемление (рис. 108).

В опорах возникают силовые факторы, называемые реакциями опор. Два первых вида шарнирных опор допускают свободное проворачивание балки, и поэтому в них не возникает опорных моментов. Только жесткая заделка, не допускающая поворота балки в опоре, создает реактивный опорный момент.

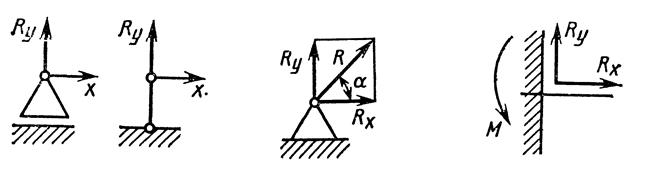
Рис. 106. Шарнирно - Рис. 107. Шарнирно - Рис. 108. Жесткая заделка

подвижная опора неподвижная опора или защемление

Подвижная шарнирная опора допускает свободное осевое перемещение балки на катках, поэтому в ней возникает только одна опорная реакция.

В неподвижной шарнирной опоре возникает реакция под углом α к горизонтальной оси, эта реакция может быть разложена на две реакции в горизонтальном и вертикаль-

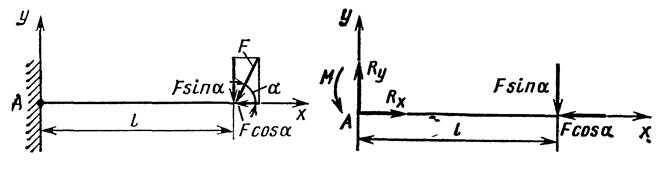
Рис. 109. Консольная балка под Рис. 110. Расчетная схема кон-
нагрузкой сольной балки

ном направлениях. Угол α определяет отношение величин горизонтальной и вертикальной составляющих реакций опор:

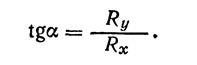
Жесткая заделка, или защемление, дает три реакции: R_x, R_y , M.

Рассмотрим, например, балку, нагруженную силой F, защемленную с одной стороны, и свободную с другой (рис. 109). Такую балку называют консольной. Ось у направим вертикально, а ось х — горизонтально.

Действующую под углом α силу F разложим по осям х и у на F cos α и F sin а (см. рис. 109). В защемлении возникают три неизвестные реакции: две силы R„ и R_K и момент М. Приложим к балке неизвестные опорные реакции и получим расчетную схему (рис. 110). Балка находится в равновесии, и поэтому должны быть справедливы три уравнения равновесия

ΣМ = 0, ΣF_y = 0 , ΣF_x = 0 .

Подставим в эти уравнения силы и моменты, действующие на консоль:

ΣF_y = R_y — F sin α = 0 ,

ΣF_x = R_x – F cosα = 0

ΣМ = М — Fl sin α = 0.

Момент взят относительно точки А для простоты, чтобы исключить моменты от неизвестных опорных реакций R_x и R_y . Определим

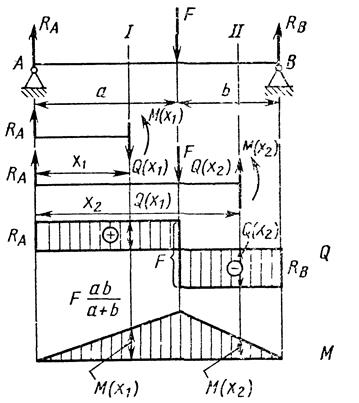
Рис. 111. Действие силы на двухопорную балку

R_y= F sin α ; R_x = F cos α ; М = F l sin α.

Из рассмотрения этого примера следует, что если действующие силы будут перпендикулярны оси балки, т. е. угол α = 90°, то горизонтальных составляющих опорных реакций не будет: cos α = 0 , R_x = 0.

Теперь можно перейти к рассмотрению способов построения графиков изменения внутренних силовых факторов при изгибе Q и М по длине балки или эпюр Q и М.

Предварительно рассмотрим несколько простейших примеров. Некоторые из них приведены в приложении III.

Пример 1. Построить эпюры Q и М при изгибе балки на двух опорах или двухопорной балки под действием сосредоточенной силы F (рис. 111).

Решение. Определим опорные реакции Ra и R_b из уравнений равновесия балки

ΣМ_А = F a — R_B (а + b) = 0,

ΣF = R_A — F + R_B = 0

Из первого уравнения найдем R_B

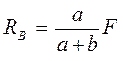
а из второго уравнения определим R_A

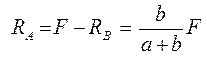
Разобьем балку на два участка и запишем выражение поперечных сил и изгибающих моментов для каждого из участков с учетом выве­денных выше соотношений и принятых правил знаков:

для участка I на рас­стоянии х₁ от опоры А

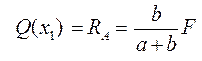
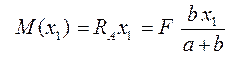
Где 0 ≤ x₁ ≤ a

При x₁ = 0 М (0) = 0,

При х₁ = а

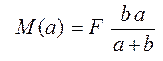
Рис. 112. Действие изгибающего

момента на двухопорную балку

для участка II на расстоянии х₂ от опоры А

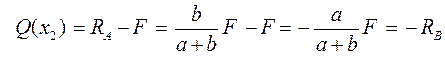
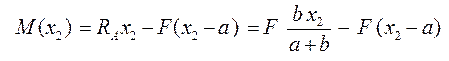
Где 0 ≤ x₁ ≤ a + b

при x₂ = a

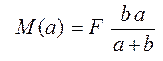
при x₂ = a + b M(a + b) = 0

Таким образом, на каждом участке балки Q постоянно, причем для участка

I — положительно, а для II — отрицательно, а момент имеет линейную зависимость от х и на участке I возрастает от 0 до 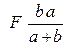,а на участке II убывает от этой величины до нуля. С учетом этого по­строим эпюры Q и М (см. рис. 111). Следует отметить, что там, где действует сила, на эпюре поперечных сил наблюдается скачок, равный по величине действующей силе. Так, на эпюре Q имеется три скачка там, где действуют силы R_a , F и R_b .

Если сила имеет знак плюс, скачок наблюдается вверх, если ми­нус — вниз, в случае действия силы F.

Определим связь ме­жду нормальным напря­жением при изгибе балки σ и изгибающим момен­том М. Рассмотрим усло­вия чистого изгиба балки (рис. 114), когда Q = 0 и в сечении действует
только изгибающий момент. Опыт показывает, что соотно-шение для σ при чистом изгибе можно использовать для опреде-ления нормальных напряжений при поперечном изгибе.

Рассмотрим положение двух плоскостей I , II , лежа­щих друг от друга на малом расстоянии dx (см. рис. 114). При изгибе так же, как и при растяжении и кручении,

Рис 114. Деформация бруса при справедлива гипотеза плоских

чистом изгибе сечений. Сечения I и II, плоские до изгиба, остались плоскими и после изгиба (I' и II'). Только при этом повернулись на некоторый малый угол dφ, оставаясь перпендикулярными к н аружным

поверхностям балки. При этом верхние волокна балки растянулись, их длина а'b' стала больше прежней ab, а нижние волокна балки тп сжались и приняли положе­ние т'п'.

Логично предположить, что между верхними и ниж­ними волокнами имеется линия раздела 1—2, называе­мая нейтральным слоем, который при изгибе не будет менять своей длины. При чистом изгибе он примет форму дуги окружности радиуса р. Рассмотрим деформацию произвольного волокна cd балки на расстоянии у от ней­трального слоя 1—2 (рис. 115). Проведем из точки 2 прямую 2е, параллельную 1с, тогда ed будет равна удлинению волок­на cd. Ввиду малости угла dφ определим дуги ed и 1 — 2: ed = y dφ ; 1 — 2 — ρ dφ , откуда следует

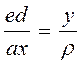
если учесть, что dx — длина волокна cd до деформа­ции (см. рис. 114), то станет ясно, что ed /dx является де­формацией волокна cd:

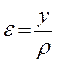
Полученная зависимость показывает что деформация волокна прямо пропорциональна её расстоя-нию y от нейтрального слоя. Максимальные деформации балка испытывает в

точках поперечного сечения

Рис. 115 Деформация волокон бруса при

изгибе

максимально удаленных от нейтрального слоя. Для определения напряжений воспользуемся законом Гука

σ = Е ε

откуда следует после подстановки соотношение

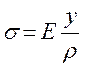
Нормальное напряжение в поперечном сечении при изгибе балки прямо пропорционально расстоянию от ней­тральной оси балки. Пользуясь этой зависимостью, можно построить эпюру распределения нормальных напряжений по сечению балки (рис. 116). В нейтральном слое не возникает ни нормальных напряжений, ни деформаций. Линия пересечения нейтрального слоя с поперечным сечением балки называется нейтральной осью.

Определим положение нейтральной оси. Для этого вспомним, что в поперечном сечении сумма всех сил на ось х равна нулю, так как при изгибе балки продольных сил нет.

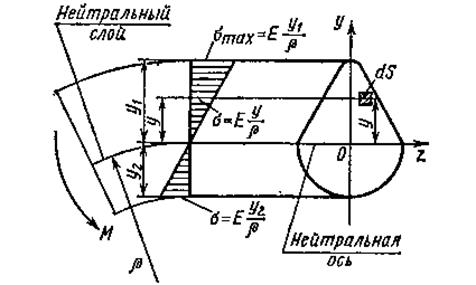
Рис. 116. Эпюра нормальных напряжений при изгибе

Продольная элементарная сила, действующая на эле­ментарную площадку dS,

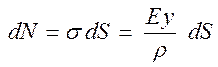
Просуммировав по всей площади, получим

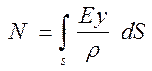
С учетом того, что постоянная величина 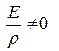, следует равенство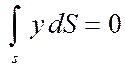

Ранее при рассмотрении геометрических характери­стик сечений было показано, что это равенство не что иное, как равенство нулю статического момента пло­щади сечения относительно оси z : S = 0, что свидетель­ствует о том, что нейтральная ось проходит через центр тяжести сечения 0 (см. рис. 116).

Для количественного определения напряжений необ­ходимо найти радиус кривизны нейтрального слоя де­формированной балки r. Запишем очевидное равенство действующего в сечении изгибающего момента М моменту от нормальных сил. Элементарная нормальная сила на расстоянии у от нейтральной оси, действующая на эле­ментарную площадку dS,

dN = s dS,

а элементарный момент относительно нейтральной оси

dM = s y dS.

Суммируя элементарные моменты по площади сечения и подставляя выражение 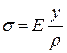, найдем

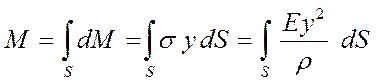
Отсюда определим кривизну изогнутой оси бруса

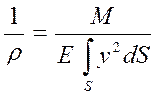
Где 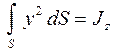— момент инерции поперечного сечения относительно оси z.

Подставим выражение кривизны в формулу для s и окончательно после элементарных преобразований по­лучим

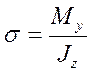
Поскольку нас больше всего интересует максимальное напряжение, то из эпюры изгибающих моментов необхо­димо найти максимальный изгибающий момент M_max и для поперечного сечения, соответствующего М_mах, найти максимальные нормальные напряжения по формуле

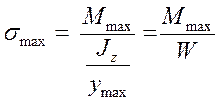
Где 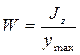— момент сопротивления изгибу.

Формулы для определения момента сопротивления основных сечений изгибу приведены в табл. Эти формулы встречаются в расчетной прак­тике. Числовые значения моментов сопротивления для стандартных профилей проката указаны в соответствую­щих ГОСТах на прокат.

Момент сопротивления изгибу измеряется в м³. Если материал балки пластичный, например, сталь, то условие прочности определяется по максимальному напряжению

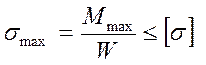
В случае хрупкого материала (чугун) требуется про­верка прочности по напряжениям, как растяжения, так и сжатия:

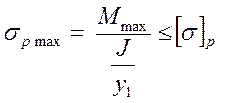
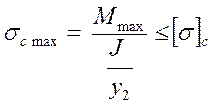
С учетом условий прочности решаются три основные задачи:

1) задача проверки прочности — по заданным нагруз­кам и геометрическим размерам поперечного сечения оп­ределяют максимальное напряжение в сечении, называе­мом опасным

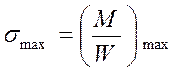
и оно сопоставляется c допускаемым [s ] ;

2) проектная задача, когда по заданным нагрузкам и допускаемым напряжени-ям определяют поперечное се­чение балки, исходя из момента сопротивления изгибу:

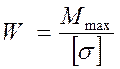
3) задача определения допускаемой нагрузки

[ М] = W [s ],

где [М] — допускаемая нагрузка, определяемая по опас­ному сечению балки.

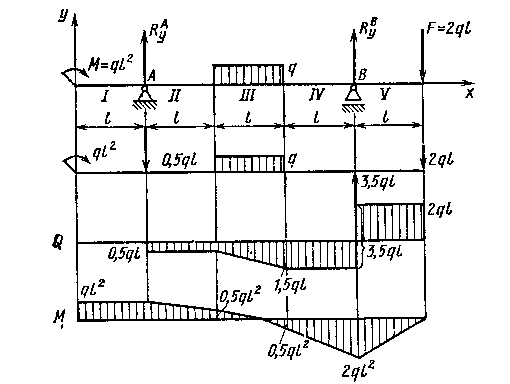
Рис. 117.Эпюра изгибающих моментов М и перерезывающих сил

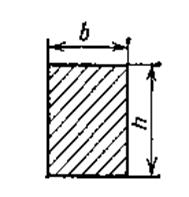
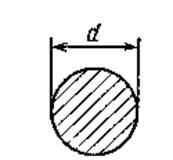
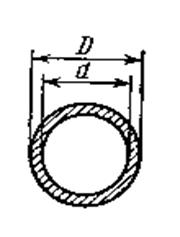
Таблица 1. Формулы для определения момента сопротивления изгибу

основных сечений

Сечение	Формула момента сопротивления изгибу W

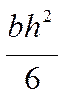
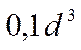
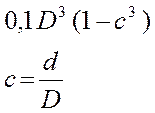
ЛЕКЦИЯ 31

Тема 2.6. Понятие о касательных напряжениях

при изгибе. Линейные и угловые перемещения

при изгибе, их определение

Иметь представление о касательных напряжениях при изги­бе, об упругой линии балки, о деформациях при изгибе и методах определения линейных и угловых перемещений.

Знать один из методов определения линейных и угловых пере­мещений.