Метод начальных параметров
Метод начальных параметров получил широкое применение при решении различных инженерных задач. Его разработали советские ученые Н.П. Пузыревский, Н.К. Снитко, Н.И. Безухое, А.А. Уманский и др.
Для того чтобы сократить число неизвестных произвольных постоянных интегрирования до двух, необходимо обеспечить равенство соответствующих постоянных на всех участках балки. Это равенство будет соблюдаться, если в уравнениях моментов, углов поворота и прогибов при переходе от участка к участку повторяются все силовые факторы предыдущего участка, а вновь появляющиеся слагаемые обращаются в нуль на левых границах своих силовых участков. Для обеспечения этих условий при составлении дифференциальных уравнений упругой линии и их интегрировании должны соблюдаться следующие условия:
1. Начало координат (общее для всех силовых участков) выбирается на конце балки:
- если есть заделка, то в заделке;
- если на конце есть опора, то на опоре;
- если на обоих концах консоли, то безразлично, на каком конце начало координат.
2. При составлении уравнения для конкретного сечения учитываются нагрузки, расположенные от начала координат до сечения; распределенная нагрузка q продолжается до сечения в соответствии с правилами Клебша. При наличии сосредоточенного момента М его значение представлять в виде произведения М(z - l)0, где l – расстояние от начала координат до сечения, в котором этот момент приложен.
3. При действии распределенной нагрузки, не доходящей до правого конца рассматриваемого участка, она продолжается до этого конца и одновременно уравновешивается противоположно направленной нагрузкой той же интенсивности («дополнительная» и «уравновешивающая» нагрузки показываются на рисунках штриховыми линиями).
4. Интегрировать уравнение на всех участках, не раскрывая скобок.
Рассмотрим балку (рис. 7.2) с постоянным поперечным сечением, нагруженную взаимоуравновешенной системой положительных силовых факторов (т.е. вызывающих вертикальные перемещения сечений балки в положительном направлении оси z). Начало системы координат поместим на левом конце балки так, чтобы ось x проходила вдоль оси балки, а ось z была бы направлена вверх.
На балку действуют: момент М, сосредоточенная сила F и равномерно распределенная на участке бруса нагрузка интенсивностью q (рис. 7.2).
| z |
| F |
| l |
| x |
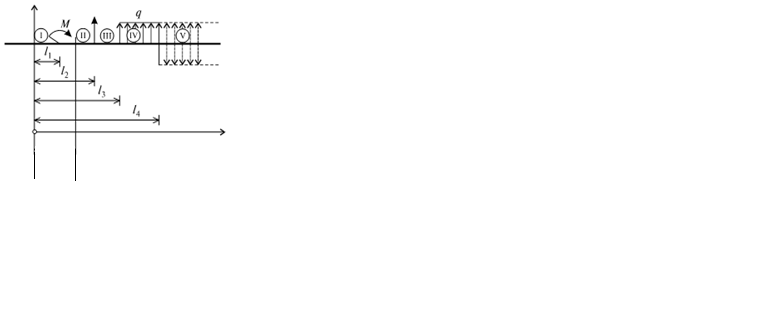
Рис. 7.2
Задача заключается в том, чтобы выявить особенности, вносимые в уравнение упругой линии, различными типами внешних силовых факторов. Для этого составим выражение изгибающих моментов для каждого из пяти участков заданной системы.
| x |
Участок II (l1 £ x £ l2 ) My (x) = M.
Участок III (l2 £ x£ l3 ) My (x) = M + F (x - l2).
Участок IV (l3£ x£ l4) My (z) = M + F (x - l2) + 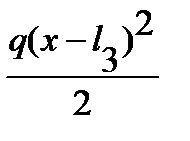 .
.
Участок V (l4 £ х £ l5) Mу (х) = M + F (х - l2) + 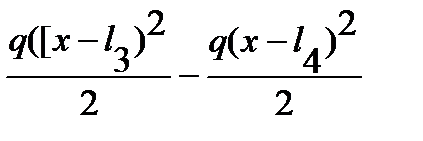 .
.
На участке V, где распределенная нагрузка отсутствует, при выводе выражения для изгибающего момента с целью сохранения рекуррентности формул для разных участков была приложена взаимоуравновешенная распределенная нагрузка.
Для вывода обобщенного выражения изгибающего момента введем следующий оператор 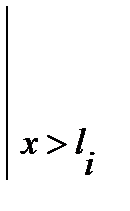 , означающий, что члены выражения, стоящие перед ним, следует учитывать при х> li и игнорировать при х £ li . На основании этого обобщенное выражение момента Mу (х) для произвольного сечения х может быть записано единой формулой:
, означающий, что члены выражения, стоящие перед ним, следует учитывать при х> li и игнорировать при х £ li . На основании этого обобщенное выражение момента Mу (х) для произвольного сечения х может быть записано единой формулой:
Mу(х) = M 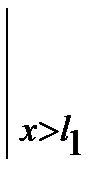 +F (х - l2)
+F (х - l2) 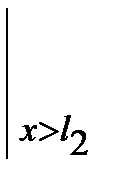 +
+ 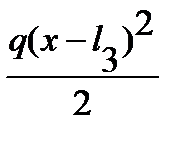

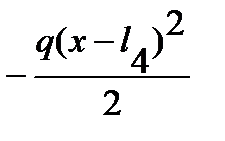
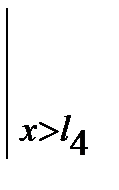 . (7.4)
. (7.4)
Подставляя (7.4) в (7.3) и дважды интегрируя, получим выражение для прогибов:
E Iу z (x) = C0 + C1 x+ 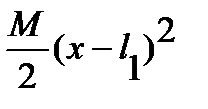
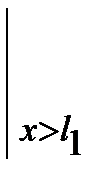 +
+ 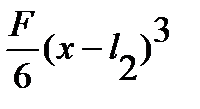
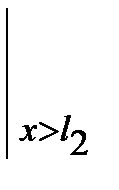 +
+ 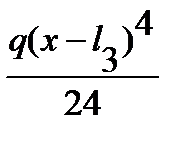
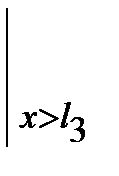 -
-
- 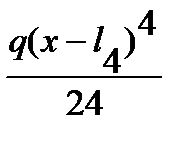
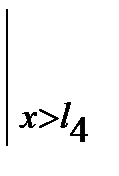 . (7.5)
. (7.5)
Постоянные интегрирования C0 и C1 по своей сути означают:
C0 = E Iy z (0) , C1 = 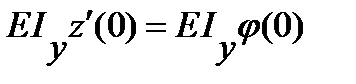 (7.6)
(7.6)
и определяются из граничных условий на левом конце балки. Тогда формула для прогибов примет следующий окончательный вид:
E Iy z(x) = E Iyz0 + 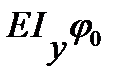 x +
x + 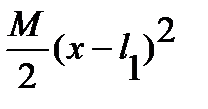
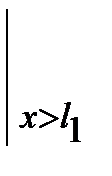 +
+ 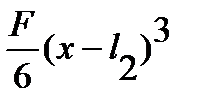
 +
+
+ 
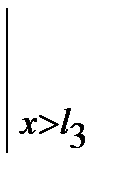 -
- 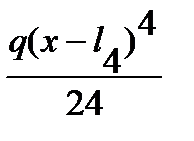
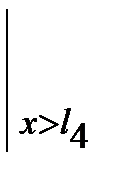 . (7.7)
. (7.7)
Соответственно формула для углов поворотов сечений балки определяется из (7.7) простым дифференцированием:
E Iy j (x) = 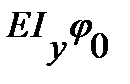 +
+ 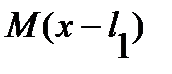
 +
+ 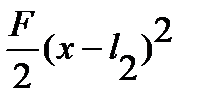
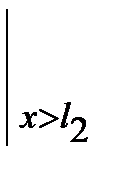 +
+ 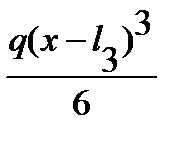
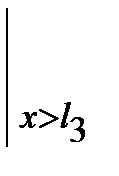 -
-
– 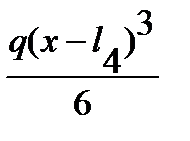
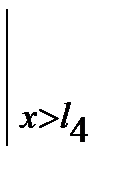 . (7.8)
. (7.8)
Как видно, для определения прогибов и углов поворота балок данным методом начальных параметров достаточно знание лишь значений прогиба z0 , угла поворота j0 в начале системы координат, т.е. так называемых начальных параметров. Поэтому данный метод и называется методом начальных параметров.
Дата добавления: 2015-08-21; просмотров: 1922;
