Косой изгиб. Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.
Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.
Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как сочетание двух плоских изгибов во взаимно перпендикулярных плоскостях (рис. 8.1).
| Рис. 8.1 |
| y |
| My |
| z |
| Mz |
| j |
| M |
| y |
| z |
Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов My и Mz:
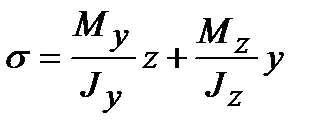 , (8.1)
, (8.1)
где 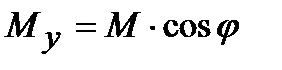 ,
, 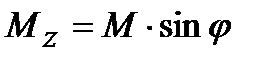 ;
;
j – угол отклонения плоскости действия M от вертикали.
Для определения положения опасной точки сечения и записи условия прочности необходимо записать уравнение нейтральной линии (н.л.) как геометрического места точек сечения, в которых напряжения равны нулю.
Уравнение нейтральной линии имеет вид:
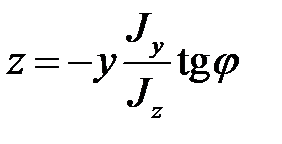
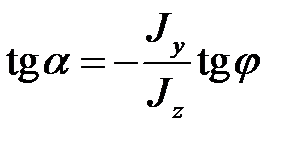
, или .
| D |
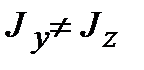 , то плоскость действия момента М и нейтральная линия не перпендикулярны друг другу (в отличие от плоского изгиба).
, то плоскость действия момента М и нейтральная линия не перпендикулярны друг другу (в отличие от плоского изгиба).
Максимального значения в сечении нормальные напряжения достигают в наиболее удаленных от нейтральной линии точках В и D (рис. 8.2).
Эти точки являются опасными в данном сечении.
Условие прочности в т. B имеет вид:
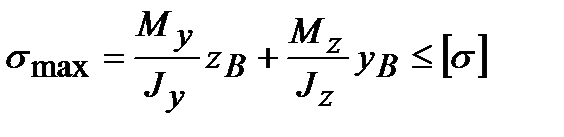 , (8.2)
, (8.2)
где zB, yB – координаты точки B.
Для сечений, вписывающихся в прямоугольник (швеллер, двутавр и др.), в
точках с координатами ymax и zmax, условие прочности может быть записано в виде
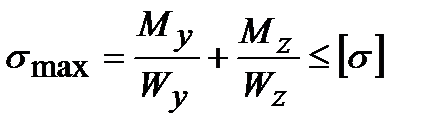 . (8.3)
. (8.3)
Прогиб при косом изгибе определяется как геометрическая сумма проги-
бов вдоль осей 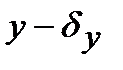 и
и 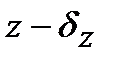 (рис. 8.3) по формуле
(рис. 8.3) по формуле 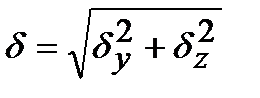 .
.
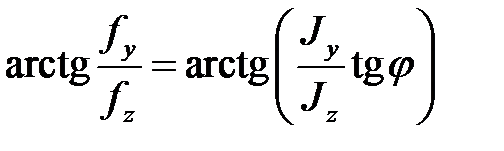 Направление прогиба определяется углом
Направление прогиба определяется углом
.
Из формулы видно, что направления прогиба балки будет совпадать с плоскостью действия момента при Jz = Jy . Если моменты инерции сечения не равны между собой 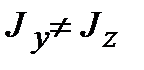 , то направление прогиба и положение плоскости действия момента не совпадают (рис. 8.3).
, то направление прогиба и положение плоскости действия момента не совпадают (рис. 8.3).
| н.л |
| j |
| M |
| y |
| z |
| a |
| s |
| B |
| Рис.8.2 |
| н.л. |
| j |
| M |
| у |
| z |
| dу |
| dz |
| d |
|
| Рис. 8.3 |
Дата добавления: 2015-08-21; просмотров: 1772;
