НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ

Этот расчет является основным для зубьев открытых передач*. На изгиб рассчитывают также зубья закрытых передач при высокой поверхностной твердости зубьев.

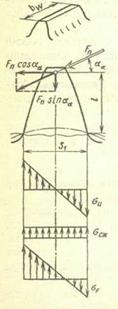
Прямозубые и косозубые цилиндрические передачи. Точный расчет зуба возможен лишь методами теории упругости. В инженерном расчете зуб рассматривают как консольную балку постоянного сечения (рис. 20.28) и по формулам сопротивления материалов определяют номинальные напряжения. Уточнение расчета произво­дится, как обычно, введением теоретического коэффициента концентрации напряжений.

Прямозубые передачи. В расчете полагаем, что усилие в зацеплении передается лишь одной парой зубьев, что справедливо для колес 8-й степени точности и более низкой. Ошибки их изготовления не гарантируют наличия двухпарного зацепления, зуб нагружен силой F_n направленной по линии зацепления. Влиянием сил трения пренебрегаем ввиду их малости (коэффициент трения при наличии в контакте смазочного материала ).

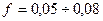Рис. 20.28. К расчету на изгиб зуба

........................................

* Внастоящее время используют редко, лишь в случаях, когда уста­новка колес в защитный кожух или специальный корпус связана со зна­чительными конструктивными и технологическими трудностями.

Силу F_n, не внося больших погрешностей, можно перенести на ось симметрии. Под действием силы F_n в опасном сечении (у основания) зуба будут действовать изгибающий момент М_и, перерезывающая Q и продольная (сжимающая) F_сж силы:

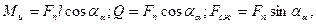
где 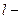плечо изгибающего усилия.

Напряжения изгиба, возникающие в крайних волокнах опасного сечения (у основания зуба):

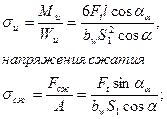
здесь М_и и F_сж — изгибающий момент и сжимающая сила; W_и и А — момент сопротивления изгибу и площадь сечения зуба; 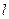— плечо изгибающего усилия; S₁ — толщина зуба в опасном сечении; 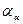— угол направления усилия 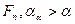(см. рис. 20.8, 20.23). Касательные напряжения в крайних волокнах модели зуба равны нулю. При написании последних равенств сила F_n выражена через окружную силы F_t , действующую на делительной окружности [см. формулу (20.15)]. Суммарное номинальное напряжение на растянутой стороне в опасном сечении

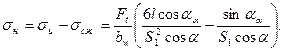
Отметим, что напряжения на растянутой стороне меньше, чем на сжатой. Однако экспериментально установлено, что поверхностные слои материала зуба оказывают меньшую сопротивляемость переменным растягивающим напряжениям, чем напряжениям сжатия. Поэтому наиболее опасны напряжения, возникающие на растянутой стороне зуба.

Последнее соотношение представим в виде

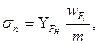(20.21)

где 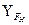— коэффициент формы зуба при расчете по номинальным напряжениям; т — модуль зуба; 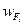— удельная расчетная окружная сила¹

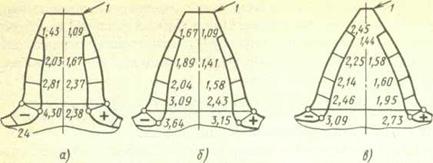
Рис. 20.29. Распределение относительных напряжений на контуре зубьев 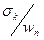( 1Н/мм) колес (m= 1 мм,z=40) при различных смещениях:

а - х = -1; б - х = 0; в - х = 1

С учетом формулы (20.20) при 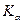=1

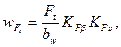(20.22)

где - коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба (табл. 20.1); K_Fv -коэффициент динамической нагрузки (см. табл. 20.2, ).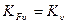

Безразмерный коэффициент

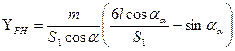
равен номинальным растягивающим напряжениям в основании зуба с модулем т = 1 мм при окружной силе w_Ft = 1 Н/мм.

Из-за концентрации напряжений, вызванной изменением формы тела вблизи переходной поверхности, местные на­пряжения 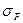будут больше номинальных 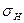(рис. 20.29). Концентрация напряжений вблизи переходной поверхности и в зоне контакта хорошо видна на картине полос (рис. 20.30), полученной методом фотоупругости (наибольшие напряжения соответствуют наибольшей частоте полос).

Местные напряжения в опасном сечении

где — теоретический коэффициент концентрации напряжений, или с учетом равенства (20.21)

……………………….

¹ Здесь и далее индекс F указан для параметров, связанных с расчетом напряжений изгиба в зубьях передач.

Рис. 20.30. Интерференционные полосы при статическом изгибе модели зуба из оптически активного материала

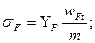(20.23)

здесь 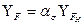— коэффициент формы зуба. Зависимость 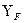от числа зубьев z и коэффициента смещения х приведена на рис. 20.31.

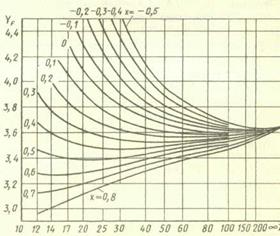
Рис. 20.31. Зависимость коэффициента формы зуба по местным напряжениям YF от числа зубьев г и коэффициента смещения х при приложении нагрузки к вершине зуба при исходном реечном контуре по ГОСТ 13755 — 81

Косозубые передачи¹. У косозубых передач суммарная длина контактных линий 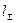больше ширины колеса 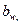что приводит к пропорциональному снижению напряжений изгиба.

Для косозубых передач

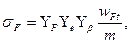(20.24)

где 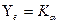-коэффициент, учитывающий перекрытие зубьев; 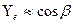— коэффициент, учитывающий наклон зубьев,

С учетом зависимости (20.20) условие прочности зуба по допускаемым напряжениям примет вид

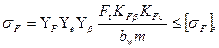
(20.25)

где 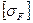— допускаемое напряжение изгиба (см. ниже).

Выразим неизвестную окружную силу F_t через вращающий момент на шестерне Т₁ (в Н• м) и примем, что ширина колеса 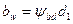,тогда из условия (20.25) после несложных преобразований получим

(20.26)

где K_m — коэффициент, при средних значениях величин , и K_Fv можно принимать:

К_т = 14 - для прямозубых передач, 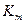= 11,2 -для косозубых передач; 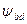- коэффициент ширины колеса, 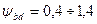- для колес, расположенных между опорами (большее значение берется для колеса в середине пролета); 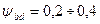— для колес на консоли; Y_Fl — коэффициент формы зуба шестерни. Для косозубой шестерни Y_Fl принимают также из рис. 20.31 для числа зубьев эквивалентного прямозубого колеса z_lv (см. с. 334).

Значение модуля округляют до ближайшего значения из ряда модулей по ГОСТ 9563-60 и по принятому значению модуля находят размеры колес (см. с. 328). Ширина шестерни в прямозубой передаче выполняется несколько больше номинальной ширины

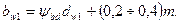
Для косозубых колес должно быть

.

^{…………………………………………}

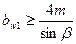¹ При наличии абразивного изнашивания суммарная длина контактных линий уменьшается, поэтому косозубая передача в качестве открытой не используется.

Для компенсации неточностей установки в осевом направлении ширина колеса делается несколько уже шестерни

b_w2 = b_wl - (0,2 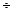0,4) m.

Значения b_w1 и b_w2 округляют по ГОСТ 6636 — 69.

Из формулы (20.26) видно, что модуль и, как следствие, габариты передачи могут быть уменьшены главным образом за счет повышения прочности материала колес, а также пу­тем уменьшения концентрации нагрузки вдоль зуба (уменьше­ния и увеличения ).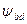

Мелкомодульные колеса предпочтительны по условиям плавности хода и экономичности, однако крупномодульные колеса менее чувствительны к перегрузкам, неоднородности материала и погрешности их изготовления в меньшей сте­пени влияют на прочность зубьев. Поэтому для силовых передач принимать т < 1,5 мм не следует.

Конические передачи.Их расчет аналогичен расчету пря­мозубой цилиндрической передачи.

Условие прочности зуба конического колеса имеет вид

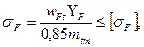(20.27)

где w_Ft — расчетная удельная окружная сила; Y_F — коэффициент формы зуба, определяется по графику на рис. 20.31 при эквивалентном числе зубьев [ 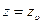см. с. 336];

0,85 — экспериментальный коэффициент, учитывает пониженную нагрузочную способность конических передач по сравнению с цилиндрическими из-за конструктивных особенностей; т_tm — модуль в среднем нормальном сечении зуба.

Основными (чертежными и производственными) размерами для конических колес являются размеры на большем торце. Модуль в этом сечении (см. рис. 20.18)

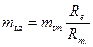
Способ нарезания конических колес не требует стандартизации модулей т_tа и т_tm и они могут иметь любое значение. Для удобства контроля размеров желательно выбирать полученное из расчета и округленное до стандартного (ГОСТ 9563-60) значение т_ta.

Отметим, что в качестве расчетного принято среднее сечение зуба. Между тем расчет можно отнести к любому сечению, так как все поперечные сечения зуба остаются геометрически подобными и удельная нагрузка линейно возрастает пропорционально удалению сечения от вершины делительного конуса.

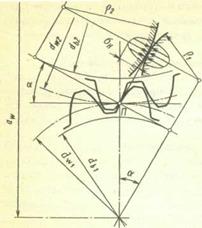
Рис. 20.32. К расчету контактной прочности зубьев