ОСОБЕННОСТИ
РАСЧЕТА И ПРОЕКТИРОВАНИЯ
ПЛАНЕТАРНЫХ ПЕРЕДАЧ
Устройство и основные кинематические и силовые соотношения.Планетарными называют передачи, которые имеют хотя бы одну подвижную геометрическую ось зубчатого колеса.
Подвижность оси позволяет уменьшить габариты передачи и получить систему с двумя (и более) степенями свободы. На рис. 20.33, а показана кинематическая схема передачи из двух цилиндрических колес 1 и 2 с неподвижными осями. Подвижность оси одного из колес, например колеса 1, можно задать, если корпус подшипников этого колеса связать с вы- ходным валом, соосным с входным валом (рис. 20.33,б). В полученной планетарной передаче колесо 2 с неподвижной осью называют центральным, выходной вал вместе с корпусом подшипников промежуточного вала — водилом, а колесо с подвижной осью — сателлитом. Колесо 2 можно выполнить неподвижным, а вращение колесу 1 передать через двойной универсальный шарнир 4 (рис. 20.33, в). Тогда, обкатываясь по колесу 2, колесо 1 будет увлекать за собой водило.
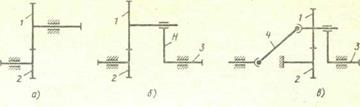
Рис. 20.33. К образованию планетарного механизма
Аналогичный механизм показан на рис. 20,34, а. Здесь сателлит 2 имеет внешнее и внутреннее зацепление соответственно с центральным (иногда называемым солнечным) колесом 1 и неподвижным колесом 3 (соединенным с неподвижным корпусом механизма).
Для кинематического анализа планетарных передач используют обычно метод остановки водила (метод Виллиса). При этом всей планетарной передаче сообщается (мысленно) вращение с угловой скоростью водила соя, т. е. водило мысленно останавливается, а другие звенья освобождаются. Полученный механизм с обычной передачей называют обращенным.
Мысленная остановка водила равноценна вычитанию его угловой скорости из скоростей подвижных колес. Тогда передаточное отношение для передачи на рис. 20.34, а, имеющей три выходных звена:
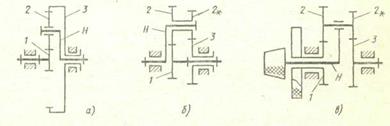
Рис. 20.34. Кинематические схемы планетарных механизмов
(20.36) 
оно представляет собой отношение угловых скоростей в движении относительно водила. В формуле (20.36): 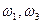 и
и 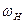 — угловые скорости колес I, 3 и водила H; нижние индексы при i показывают ведущее и ведомое звено, верхний — мысленно остановленное звено.
— угловые скорости колес I, 3 и водила H; нижние индексы при i показывают ведущее и ведомое звено, верхний — мысленно остановленное звено.
Учитывая, что в рассматриваемом механизме колесо 3 неподвижно ( 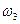 = 0), получим
= 0), получим
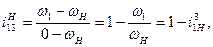
 (20.37)
(20.37)
откуда

Если z1 z2 и z3 — числа зубьев колес 1, 2 и 3, то 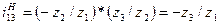 и окончательно будем
и окончательно будем 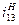
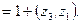 Знак минус в первом множителе показывает, что вращение ведомого колеса 2 происходит в направлении, противоположном вращению колеса 1. В передаточное отношение
Знак минус в первом множителе показывает, что вращение ведомого колеса 2 происходит в направлении, противоположном вращению колеса 1. В передаточное отношение 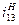 не входит z2, так как в этой схеме сателлит является паразитным колесом.
не входит z2, так как в этой схеме сателлит является паразитным колесом.
Рассмотрим другой подобный механизм (рис. 20.34,6), в котором сателлит выполнен (двухвенцовым) сдвоенным, а оба зацепления внешними1. Эта передача также имеет три выходных звена, для нее из формулы (20.37) получим ( 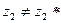 ).
).
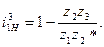
Если взять 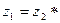 =100, z2 = 99 и z3 =101, то
=100, z2 = 99 и z3 =101, то 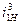 = 0,0001. Если ведущим звеном будет водило H, то
= 0,0001. Если ведущим звеном будет водило H, то

Этот пример показывает возможности получения в планетарной передаче больших и малых передаточных отношений. Описанный планетарный механизм можно использовать для суммирования и разделения движения в верньерных устройствах приборов. В схеме на рис. 20.34, в грубая настройка прибора (быстрый поворот колеса 3) осуществляется при вращении звена 1, а точная настройка (медленный поворот колеса 3) — за счет вращения водила Н малой ручкой. При этом в первом случае происходит самоблокировка передачи, например, за счет прижатия водила H к колесу 1 или 3 с помощью пружины (на схеме не показана). Во втором случае колесо 1 останавливают, например, за счет прижатия его к корпусу пружиной. Хотя в таких механизмах КПД невелик, это не влияет на качество системы в целом.
…………………………………………..
1 Схемы планетарных передач разнообразны, здесь рассмотрены простейшие.
Коэффициент полезного действия. Планетарные передачи имеют более низкий КПД из-за увеличения относительных перемещений звеньев, вызванных подвижностью осей. С увеличением передаточного отношения КПД снижается. Для передачи с двухвенцовым сателлитом (см. рис. 20.34, б):
i………………30 50 100 200 500 1000
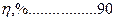 75 60 45 25 12
75 60 45 25 12
Для схемы на рис. 20.34, а 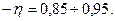 .
.
Особенности геометрии передач. Особенности геометрии обусловлены их соосностью и наличием промежуточных колес (сателлитов), поэтому собрать передачу и обеспечить правильное зацепление колес можно лишь при выполнении ряда условий.
Условие соосности записывают в виде
aw1 = aw2,
где awl и aw2 — межосевые расстояния для первой и второй пар зубчатых колес. Для передачи на рис. 20.34, а это условие приводит к равенству z3 — z1 = 2z2, а для передачи на рис. 20.34, б — z1 + z2 = z2* +z3.
Условие соседства. При установке в водиле нескольких сателлитов они не должны касаться вершинами зубьев. Если располагать их на одинаковом расстоянии, то угол между их осями 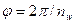 (nw — число сателлитов, рис. 20.35, а) и расстояние между ними
(nw — число сателлитов, рис. 20.35, а) и расстояние между ними
АА* = 2АВ = aw sin 
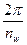 >da2.
>da2.
Число сателлитов в передаче зависит от соотношения диаметров окружностей центральных колес. Например, на рис. 20.35, а нельзя разместить больше трех сателлитов. Если же уменьшить диаметр сателлитов и увеличить диаметр внутреннего центрального колеса, то предельное число сателлитов можно увеличить (рис. 20.35, б). Обычно число сателлитов принимают меньше предельного, но не меньше трех. Это связано с усложнением передачи и трудностью обеспечения жесткости водила. Обычная форма водила показана на рис. 20.35, в.
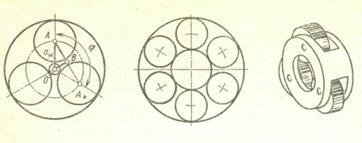
а) б) в)
Рис. 20.35. Размещение сателлитов в водиле
Условие симметричного размещения сателлитов. Чтобы установить сателлит между двумя центральными колесами (см. рис. 20.35, а), необходимо повернуть их одно относительно другого так, чтобы зубья сателлита оказались напротив впадин центральных колес. Лишь при этом условии возможна установка других сателлитов. Для передачи на рис. 20.34, а условие сборки имеет вид
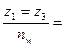 Ц,
Ц,
а для схемы на рис. 20.34, б
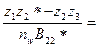 Ц,
Ц,
где Ц — любое целое число; 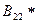 - наибольший общий делитель чисел зубьев z2 и z2*.
- наибольший общий делитель чисел зубьев z2 и z2*.
Усилия в зацеплении.Особенности расчета усилий планетарной передачи обусловлены распределением нагрузки по нескольким зубчатым зацеплениям (по числу сателлитов) и одновременном зацеплении сателлита с двумя центральными колесами (рис. 20.36). Принимают, что нагрузка между сателлитами распределяется равномерно и силы в зацеплениях одинаковы, тогда
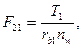
где F21 — усилие со стороны сателлита (колеса 2) на колесо 1. В действительности усилия в сателлитах не одинаковы, и это обстоятельство учитывают умножением усилия F21 на коэффициент 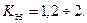 ,
,
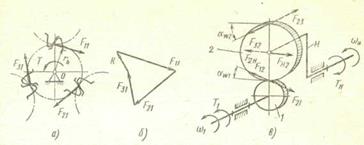
Рис. 20.36. Усилия в планетарной передаче
Участие сателлита одновременно в двух зацеплениях приводит к тому, что одновенцовый сателлит не передает вращающего момента и находится в равновесии под действием сил F12 и F32 со стороны центральных колес, а также силы FH2 от водила H (рис. 20.36, б).
Принимая, что углы зацеплений 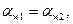 из уравнения равновесия (равенства проекций на горизонтальную ось)
из уравнения равновесия (равенства проекций на горизонтальную ось)
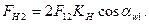
Сила FH2 используется для расчета подшипника сателлита и оси водила.
Особенности конструкции передач обусловлены наличием водила и сателлитов, конструктивные решения которых разнообразны. Наиболее характерные конструкции показаны на рис. 20.37. Водило 4 на рис. 20.37, а имеет консольные оси и для уменьшения перекосов зубьев сателлита 2 от изгиба осей его устанавливают на сферический или радиальный шарикоподшипник. В ответственных конструкциях применяют водило барабанного типа (см. рис. 20:35, в). Водило подобного типа показано на рис. 20.37, б.
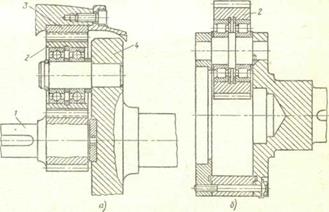
Рис. 20.37. Конструкции водила
Центральные зубчатые колеса 1 и 3 не имеют особенностей по сравнению с колесами обычных передач (с неподвижными осями).
Особенности расчета на прочность.Для расчетов на прочность используют те же формулы, что и для расчетов прямозубых цилиндрических передач. Обычно на прочность при изгибе рассчитывают только зубья внешней передачи (сателлит — наружное колесо 3, см. рис. 20.37, а), так как модули зубьев одинаковы и внутреннее зацепление прочнее. При расчете колес с внутренними зубьями коэффициент формы зуба вычисляют по формуле
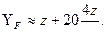
Для расчета контактных напряжений формулу (20.30) уточняют введением множителя KH/nw. В результате
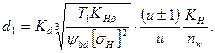
При расчете допускаемых напряжений учитывают дополнительные нагружения зубьев центрального колеса и сателлита.
Число циклов нагружений за время t (ч) для зубьев центрального колеса
NE = nw(n1 -nH)60t,
для зубьев сателлита
NE = (n2 -nH) 60t,
где п1 п2 и пH — частота вращения звеньев 1, 2 и H. Так как за один оборот одновенцового сателлита происходит нагруже-ние обеих активных поверхностей зуба, то расчет ведут как при действии реверсивной нагрузки.
Дата добавления: 2015-08-14; просмотров: 1201;
