УСИЛИЯ В ЗАЦЕПЛЕНИИ

Выше рассмотрены геометрические параметры и ки­нематические особенности взаимодействия зубьев колес. При этом полагали, что влияние деформации зубьев и тел колес на рассматриваемые параметры не существенно.

Для обоснованного назначения размеров колес и оценки их работоспособности необходимо знать меру их механического взаимодействия — напряжения и деформации и их предельные оценки (критерии работоспособности). Между тем достаточно точный расчет напряжений и деформаций в точках зубчатого колеса связан со значи­тельными математическими трудностями и может быть реализован методами теории упругости. В связи с этим на этапе проектирования выпол­няют приближенный расчет напряжений и деформаций в зубьях колес в два приема: 1) находят усилия в зацеплении — главный вектор действующих контактных давлений; 2) опре­деляют напряжения в наиболее опасных точках колеса под действием этих сил и оцени­вают прочность колеса.

При определении усилий в зацеплении используют методы теоретической механики, силами трения пренебрегают ввиду их малости.

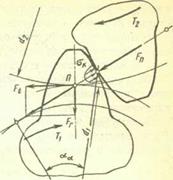
Рис. 20.23. Зацепление цилиндрических колес прямозубых

Нормальная сила между парой контактирующих зубьев (рис. 20.23)

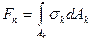
Где 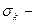контактное напряжение; 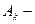площадь поверхности контакта.

Эта сила будет направлена по линии зацепления (как по общей нормали к рабочим поверхностям зубьев) так, чтобы момент этого усилия относительно оси колеса урав­новешивал бы действующий вращающий момент .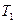

Сила 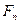является также исходной для расчета валов и поддерживающих валы опор. В этом случае, принимая для упрощения, что контакт зубьев происходит в полюсе зацепления П (его положение известно заранее), силу F_n раскладывают на составляющие.

Прямозубая цилиндрическая передача. СилуF_n раскладывают на окружную F_tи радиальную F_r составляющие. Для упрощения расчетов окружную силу в полюсе определяют по отношению к делительной окружности и обозначают F_tw:

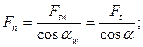
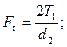
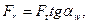(20.15)

где 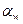- угол зацепления; 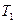- вращающий момент на ше­стерне; 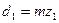- диаметр делительной окружности шестерни.

Направление действия окружной силы для шестерни про­тивоположно направлению ее вращения, а для колеса совпа­дает с направлением его вращения.

Векторы радиальных усилий у колес с внешним зацепле­нием направлены к центру, а у колес с внутренним за­цеплением — от центра зубчатого колеса.

Косозубая и шевронная цилиндрические передачи.Усилие F_nв зацеплении передачи раскладывают на окружную F_v,осевую F_aи радиальную F_r составляющие (рис. 20.24):

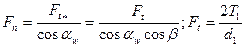; (20.16)

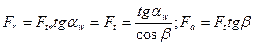
здесь 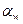- угол зацепления косозубой передачи в нормальном сечении, ; 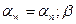-угол наклона линии зуба.

Осевая сила F_a дополнительно нагружающая опоры валов, является недостатком косозубых передач. Этот недостаток устраняется в шевронной передаче, которую можно рассматри­вать как сдвоенные косозубые передачи с противоположным направлением зубьев (см. рис. 20.14).

Для ограничения осевой нагрузки на подшипники реко­мендуют принимать для косозубых колес 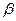<20°, а для шевронных колес 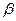< 40°.

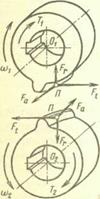
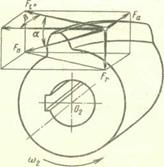
Рис. 20.24. Зацепление косозубых колес

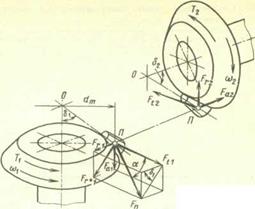
Рис. 20.25. Зацепление конических колес

Направление окружной и радиальной сил такое же, как и в прямозубой передаче. Осевая сила параллельна оси колеса, а направление вектора зависит от направления вра­щения колеса и направления линии зуба.

Прямозубая коническая передача. Взацеплении конической передачи полное усилие F_n также раскладывают на три сос­тавляющие (рис. 20.25), рассчитываемые по среднему диа­метру d_m = m_tmz (здесь m_mt -окружной модуль в среднем нормальном сечении зуба):

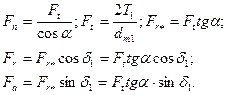(20.17)

Обратим внимание, что направление сил на шестерне и колесе противоположно, а силы F_a1 = F_r2и F_r1 = F_a2.