Г. Б. Иосилевич и др.
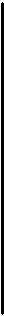 центра кривизны кривой, несложно показать, что точка N прямой NB будет центром кривизны эвольвенты (мгновенным центром вращения), а отрезок NB - радиус кривизны эвольвенты в точке В.
центра кривизны кривой, несложно показать, что точка N прямой NB будет центром кривизны эвольвенты (мгновенным центром вращения), а отрезок NB - радиус кривизны эвольвенты в точке В.
Углы развернутости v, профиля а α и эвольвентный inv α (инволюта α), образуемые радиальными прямыми ОМ, ОВ и ON, связаны между собой зависимостью
inv α = v — α.
Так как дуга MN равна отрезку BN, перекатываемому по дуге без скольжения, то (MN = rbv)
inv α = tg α — α.
Если учесть (r — радиус-вектор произвольной точки эвольвенты)
cos α = rb/r,
то становится очевидным, что радиус rb основной окружности является единственным параметром, определяющим эвольвенту. Зацепление эвольвентных профилей. Предположим, что требуется передать вращательное движение между параллельными осями О1 и 02 (межосевое расстояние аw) с постоянным передаточным отношением L Величины aw и i определяют положение полюса зацепления П на отрезке O1O2 = aw. С учетом соотношения (20.4) несложно получить
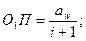 | 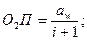 |
(20.5)
Если в качестве профиля ведущего звена 1 принять эвольвенту Э1 некоторой (произвольной) основной окружности диаметром db1 (рис. 20.7) и через полюс П провести касательную к этой окружности, то точка B1 пересечения этой касательной с профилем будет единственной точкой эвольвенты, для которой справедлив основной закон зацепления, и нормаль К эвольвенте N1П проходит через полюс. Таким образом, точка В является единственно возможной точкой контакта данного звена с сопряженным.
В других положениях звеньев точки контакта эвольвент также обязательно будут находиться на прямой, проведенной через полюс касательно к основной окружности. Линия зацепления для эвольвентного профиля является прямой' и обеспечивает эвольвентному зацеплению существенное
преимущество перед зацеплениями других видов.
1 Эвольвента — единственная кривая, дающая прямую линию зацепления.
Отметим, что прямой линии зацепления также соответствует только эвольвентный профиль, и линия зацепления является общей для обоих профилей. Таким образом, сопряженный профиль ведомого звена 2 должен быть эвольвентным и его основная окружность должна быть касательной к линии зацепления.
Перпендикуляр O2N2 из центра О2 на линию зацепления дает радиус гь2 основной окружности звена 2, определяющей эвольвенту Э2 и точку В2 на ней (совпадает с точкой Bt в данном положении).
По мере вращения звеньев с каждой точкой одного из профилей вступает в контакт вполне определенная (единственная) точка на втором профиле (см. точки Ct и С2 на рис. 20.7).
Если ввести в рассмотрение угол αw между линией зацепления и перпендикуляром к линии центров {угол зацепления), то из рис. 20.7 следует
N1П + ПN2 = N1B1 + B2N2
или
(rb1+ rb2) tg αw = rb1 vB1+ r b2vB2, (20.6)
где vB1 и vB2 — углы развернутости сопряженных точек Bt и В2 на эвольвентах.
Уравнение (20.6) позволяет найти для любой заданной точки на одном колесе сопряженную точку на другом колесе.
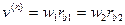 Существенно, что положение общей нормали (линии зацепления) не изменяется, и она по-прежнему будет касаться основных окружностей. Положение полюса зацепления П на линии центров также остается неизменным при вращении колес. Из рис. 20.7 видно, что в процессе зацепления точка контакта перемещается по профилю ведущего звена, удаляясь от основной окружности, а по профилю ведомого звена — приближаясь к основной окружности. Но пути, проходимые точкой контакта по каждому из сопряженных профилей за равные промежутки времени, оказываются неравными. В результате при равномерном вращении колес точки контакта, двигаясь равномерно по линии зацепления со скоростью
Существенно, что положение общей нормали (линии зацепления) не изменяется, и она по-прежнему будет касаться основных окружностей. Положение полюса зацепления П на линии центров также остается неизменным при вращении колес. Из рис. 20.7 видно, что в процессе зацепления точка контакта перемещается по профилю ведущего звена, удаляясь от основной окружности, а по профилю ведомого звена — приближаясь к основной окружности. Но пути, проходимые точкой контакта по каждому из сопряженных профилей за равные промежутки времени, оказываются неравными. В результате при равномерном вращении колес точки контакта, двигаясь равномерно по линии зацепления со скоростью
будут перемещаться (в относительном движении) неравномерно по профилям зубьев, т. е. сопряженные профили перекатываются один на другой со скольжением.
Отметим, что на каждом колесе имеется по одной соосной поверхности (цилиндр — в цилиндрической передаче), которые касаются друг друга, и в любой точке касания (контакта) вектор относительной скорости равен нулю. Эти поверхности называют начальными, а концентрические окружности, принадлежащие им,— начальными окружностями. Они описываются из центров и проходят через полюс. Из соотношений (20.5) следует, что диаметры начальных окружностей
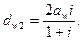
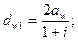 (20.7)
(20.7)
Диаметр начальной окружности связан с диаметром основной окружности соотношением (см. рис. 20.7)
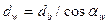 |
(20.8)
 Окружная скорость точки на начальной окружности
Окружная скорость точки на начальной окружности
Межосевое расстояние передачи можно выразить и через диаметры основных окружностей
 . (20.9)
. (20.9)
Это уравнение характеризует зацепление двух зубьев с эвольвентными профилями. В реальном зубчатом зацеплении одновременно могут контактировать несколько пар зубьев. Если ввести в рассмотрение шаг рь по основной окружности — расстояние между соседними эквидистантными профилями по дуге основной окружности, то из равенства координат сопряженных точек зубьев следует, что одновременный контакт нескольких пар зубьев возможен при условии
P b1 = Р b2,
где рb1 и р b2 — шаги по основной окружности первого и второго колес.
Из уравнения (20.9) следует также:
а) пара эвольвентных профилей с заданными диаметрами db1
и db2 может зацепляться при различных межосевых расстояниях аw
б) эвольвента заданной основной окружности dbl может
сцепляться с эвольвентами любых основных окружностей db2
при одних и тех же или при различных αw;
в) эвольвентные колеса с любыми числами зубьев могут
сцепляться друг с другом, если их шаги равны;


Рис. 20.8. Активная линия зацепления
г) эвольвентные колеса могут сопрягаться с рейкой, имеющей произвольный угол профиля, если их основные шаги равны.
Коэффициент перекрытия. Отметим точки Р1 и Р2 пересечения окружностей вершин колес с линией зацепления (рис. 20.8, а). Тогда эти точки будут обозначать начало входа и конец выхода из зацепления пары зубьев, а участок Р1Р2 соответствует активной линии зацепления.
Для сохранения свойственного эвольвентному зацеплению постоянного передаточного отношения необходимо, чтобы следующая пара зубьев вступала в зацепление в точке Р1 в тот момент (или ранее), когда точка контакта предыдущей пары зубьев придет в точку Р2 (рис. 20.8,6). Следовательно, длина активной линии зацепления должна быть не менее основного шага.
Отношение длины активной линии зацепления к основному шагу

называют коэффициентом перекрытия. Для обеспечения непрерывности вращения рекомендуется εα > 1,2.
Исходный и рабочий контуры рейки. Для единообразного изготовления зубчатых колес и обеспечения их взаимозаменяемости в передачах параметры зацепления стандартизованы. В основу стандарта положен реечный контур (рис. 20.9), так как рейка сохраняет постоянный угол зацепления в паре с колесом любого радиуса и при любом относительном положении колес.
Рис. 20.9. Исходный и рабочий контуры зубчатой рейки по ГОСТ 13755—81 (ДП — делительная прямая)
Этот контур называют теоретическим исходным контуром. Одним из основных параметров контура является модуль*
т = р/π, (20.10)
измеряемый в мм и регламентированный ГОСТ 9563-60. В соотношении (20.10): р — шаг исходного контура, расстояние между одноименными профилями соседних зубьев рейки по делительной или другой, параллельной ей прямой. Делительной прямой называют прямую, на которой теоретическая толщина зуба равна ширине впадины.
Стандартом предусмотрен широкий набор модулей, обеспечивающий потребности приборов в миниатюрных зубчатых передачах, а также потребности машин в крупногабаритных передачах.
Для модулей свыше 1 мм исходный контур (ГОСТ 13755 — 81) является прямобочным и имеет следующие параметры (рис. 20.9, а). Профильный угол α = 20°, глубина захода h1 = 2hα*m (здесь hα* = 1 — коэффициент высоты головки зуба); толщина зуба по делительной прямой S = 0,5р; радиальный зазор с — с*т (здесь с* = 0,25 — коэффициент радиального зазора) и радиус закругления у корня зуба рi = 0,384m.

 * Предпочтительный ряд значений модуля т в диапазоне от 1до 12 мм: 1;1,25; 1,5; 2; 2,5; 3; 4;5; 6; 8; 10; 12.
* Предпочтительный ряд значений модуля т в диапазоне от 1до 12 мм: 1;1,25; 1,5; 2; 2,5; 3; 4;5; 6; 8; 10; 12.
Рис. 20.10. Изготовление зубчатых колес копированием с помощью фрез (я и б)
и обкаткой с помощью долбяка и гребенки(виг):
/ — пальцевая фреза; 2 — дисковая фреза; 3 — долбяк; 4 — гребенка
Для обеспечения плавного вхождения зубьев в зацепление и снижения динамических нагрузок на вершине зубьев исходного контура преднамеренно отступают от теоретической эвольвентной формы, выполняя срез профиля — фланк (рис. 20.9, б). Расчетный контур с фланком называют номинальным исходным контуром (рабочим контуром).
Однозначность перечисленных основных параметров делает исходные контуры различных модулей геометрически подобными.
Изготовление колес. Зубчатые колеса изготовляют преимущественно методами резания на универсальных фрезерных и специальных станках. Зубья нарезают либо методом копирования, либо методом огибания (обкатки).
При использовании метода копирования впадина между зубьями вырезается специально спрофилированным инструментом — фрезой, протяжкой, шлифовальным кругом (рис. 20.10).
Для нарезания зубьев методом обкатки применяют специальный инструмент — рейку, долбяк, червячную фрезу. Инструменту и нарезаемому колесу на специальных станках сообщается такое же относительное движение, как и в реальном зацеплении. Основное преимущество такого метода изготовления — высокая точность.
Мелкомодульные зубчатые колеса иногда изготовляют накатыванием зубьев (обработкой давлением).
Точность изготовления.Для обеспечения требуемого качества передач разработаны показатели точности. Так, ГОСТ 1643 — 81 устанавливает допуски цилиндрических зубчатых передач с модулями m = 1 -г- 50 мм, обеспечивающими 12 степеней точности передач (самая низкая степень точности — двенадцатая). Требуемая степень точности определяется уровнем скоростей колес и действующих нагрузок. Быстроходные передачи (окружная скорость колеса v > 20 м/с) изготовляют с повышенной точностью (степени точности 6 и 5).
§ 5. ГЕОМЕТРИЧЕСКИЙ РАСЧЕТ ЭВОЛЬВЕНТНЫХ ПРЯМОЗУБЫХ ПЕРЕДАЧ
Размеры колеса. Рассмотрим зацепление зубчатого колеса модуля т с числом зубьев z с инструментальной рейкой в конце обработки (рис. 20.11). Предположим, что нарезание зубьев происходило при  радиальном смещении на величину тх (х — смещение рабочего контура рейки относительно колеса), что эквивалентно смещению делительной прямой (ДП) рейки относительно начальной прямой (НП) на ту же величину.
радиальном смещении на величину тх (х — смещение рабочего контура рейки относительно колеса), что эквивалентно смещению делительной прямой (ДП) рейки относительно начальной прямой (НП) на ту же величину.
Так как начальная (станочная) окружность в процессе нарезания на колесе зубьев катится без скольжения по начальной прямой рейки, то на этой окружности шаг рейки должен уместиться z раз (z — число нарезаемых зубьев), т. е.
| Рис. 20.11. Зацепление зубчатого колеса с рейкой |

| Рис. 20.12. Зубчатое зацепление в передаче без смещения |
z=nd/p.
Окружность, на которой шаг равен шагу рейки, называют делительной окружностью. Так как отношение р/π = = т, то
d = mz. (20.11)
Диаметр основной окружности
db = mz cos a,
где а — угол профиля исходного контура.
Диаметр окружности впадин (см. рис. 20.11)
df = mz - 2 (ha* + с* - х)т,
а диаметр окружности вершин
da = df + 2h = mz + 2(ha* + x)m.
Толщина зуба по делительной окружности равна ширине впадины рейки по начальной прямой

Высота зуба (рис. 20.12) h = 0,5 (da - df), высота головки зуба ha = 0,5 (da - d) и высота ножки зуба hf = 0,5 (d - df).

| Рис. 20.13. Зубья колес (z = W), нарезанных с различным смещением (первый слева - при х =—0,5, второй - при х = 0, третий - при х = 0,5) |
Из формул видно, что диаметры колес, кроме d и db, зависят от смещения производящего контура. Условно считают смещение положительным, если при изготовлении колеса делительная прямая производящей рейки не пересекает и не касается делительной окружности колеса (см. рис. 20.11). При отрицательном смещении (х < 0) делительная прямая
рейки пересекает, а при х = 0 (нарезание без смещения) касается делительной окружности колеса. Смещение изменяет форму зуба (рис. 20.13). Так, положительное смещение приводит к утолщению зуба у основания и уменьшению кривизны профиля, так как зуб очерчивается более удаленным от основной окружности участком эвольвенты. Такие изменения формы способствуют повышению его прочности.
Благодаря смещению инструмента удается снизить минимально допускаемое число зубьев на колесе без утонения (подрезания) их у основания.
Межосевое расстояние. Различают зубчатые колеса и передачи со смещением и без смещения. Передачи без смещения имеют x1= х2 = 0 (здесь х1 и х2 — смещения первого и второго колес). В таких передачах угол зацепления αw численно равен углу профиля исходного контура а, а межосевое расстояние (см. рис. 20.12)

(20.12)
В таких передачах начальные окружности совпадают с делительными (dw1 = d1 и dw2 = d).
Передачи со смещением образуются из колес, нарезанных со «смещением.
Если коэффициенты смещения колес х1 и х2 равны по величине, а знаки их противоположны, то х∑ = х1+ х2 = 0. Такая передача называется равносмещенной и для нее, как и в передаче без смещения, aw = a, αw = α и dw = d.
Если х∑≠ 0, то в такой передаче со смещением угол зацепления αw ≠α и межосевое расстояние
(20.13) 
Межосевые расстояния для стандартных редукторов стандартизованы (aw = 40; 50; 63; 80; 100; 125; 160; 180; 200; 225; 250; 280; 315; 400; 450; 500 мм). Для нестандартных передач можно не придерживаться этих значений.
Межосевые расстояния можно округлять за счет некоторого отклонения передаточного числа (за счет изменений z2).
Для «вписывания» прямозубой передачи в заданное межосевое расстояние можно воспользоваться изменением угла зацепления otw (за счет смещения), который находят из очевидного соотношения

Геометрическому расчету передачи обычно предшествует кинематический расчет (определение передаточного числа и и др.) и назначение (определение) ряда исходных параметров, с помощью которых далее находят необходимые размеры. К таким параметрам можно отнести число зубьев шестерни zt. Если принять Z1min, то и межосевое расстояние (габариты передачи) при заданных параметрах и, т и αw будет наименьшим.
При нарезании зубьев без смещения можно изготовить колесо лишь с z1min= 17. Вводя смещение инструмента, получают z1min= 12 и менее.
На практике минимальное число зубьев шестерни назначают с учетом технологических факторов, а также кинематических параметров (плавность работы и др.). Для колес, нарезаемых без смещения, в зависимости от частоты вращения п1 рекомендуется принимать:
п1,об/мин .... менее 100 100-500 500-1000 св. 1000
Z1min..................................... 17-18 18-22 22-24 24-26
При назначении числа зубьев колеса z2 — uz1 также учитывают предшествующий опыт проектирования и эксплуатации передач: при невысоких окружных скоростях колес (v < 6 м/с) и постоянной нагрузке числа зубьев колес передачи принимают кратными друг другу или с возможно большим числом общих множителей для ускорения их приработки. При высоких окружных скоростях (v > 6 м/с) и переменной нагрузке принимают взаимно простые числа зубьев или с возможно меньшим числом общих множителей.
Расчет геометрических параметров цилиндрических зубчатых передач выполняют по ГОСТ 16532 — 70.
§ 6. ОСОБЕННОСТИ ГЕОМЕТРИИ КОСОЗУБЫХ И ШЕВРОННЫХ КОЛЕС
У косозубых (рис. 20.14, а) и шевронных (рис. 20.14,6) колес зубья наклонены под некоторым угол ом р к образующей делительного цилиндра, но оси колес являются при этом параллельными.
Направление наклона линии зуба можно определить, глядя на цилиндрическую поверхность венца. Если при этом виден зуб, поднимающийся слева направо, то такое направление считают правым. Обычно зуб шестерни делают правым, а колеса — левым (направления зубьев сопряженных колес всегда противоположны).
Нарезание косозубых и шевронных колес может производиться прямозубой рейкой, как и при изготовлении прямозубых колес: наклон зуба получают соответствующим поворотом инструмента относительно заготовки на угол β. При этом профиль косого зуба в нормальном к его оси сечении будет таким же, как и в прямозубом колесе.
Картина зацепления косозубых колес в торцовой плоскости будет такой же, как и для прямозубых колес, но параметры косозубого колеса в этой плоскости будут зависеть от угла β ;
 |  |
(20.14)
 |  |
 где mt и рt- соответственно торцовые (окружные) модуль и шаг зубьев; тn и рn — то же, в нормальном к оси зуба сечении; d — диаметр делительной окружности; aw — межосевое расстояние.
где mt и рt- соответственно торцовые (окружные) модуль и шаг зубьев; тn и рn — то же, в нормальном к оси зуба сечении; d — диаметр делительной окружности; aw — межосевое расстояние.
Рис. 20.14. Косозубое (а) и шевронное (б) колеса
В передаче со смещением межосевое расстояние находят по формуле (20.13) путем замены в ней т на mt, αw на αwt и α на αt.
Нарезание косозубых и шевронных колес может производиться также и стандартной косозубой рейкой, обкатывающей заготовку в процессе резания в плоскости вращения колеса.
В косозубой рейке различают (рис. 20.15): торцовый шаг рt , нормальный рn и осевой рх и соответствующие им модули: нормальный тп, торцовый mt и осевой тх:
 |  |  |
Эти модули связаны зависимостями
 |  |
где Р — угол наклона зубьев.
Угол профиля αt в торцовой плоскости не равен углу αn в нормальном к оси зуба сечении косозубой рейки, так как при постоянной высоте зуба шаги pt и рn не равны:

Таким образом, при нарезании прямозубой рейкой колесо будет иметь стандартный нормальный модуль тп, а торцовый модуль может быть нестандартным (произвольным).
При нарезании косозубой рейкой стандартным будет лишь модуль тt , а модуль тп в общем случае может оказаться нестандартным.
Однако угол β можно выбрать таким, чтобы оба модуля оказались стандартными. Такие инструменты используются для изготовления шевронных колес.

Рис. 20.15. Контур косозубой рейки Рис. 20.16. Эквивалентное колесо
Существенно, что прочность зуба определяют его размерыи форма в нормальном к зубу сечении, образующем эллипс с полуосями c = d/2 и e = 0,5dcosβ (рис. 20.16). Радиус кривизны эллипса rv = е2/с = d/cos2β). В цилиндрическом прямозубом колесе с диаметром делительной окружности
dv = 2rv = d/(cos2 β)
форма зуба будет такой же, как и в нормальном к зубу сечении косозубого колеса. Число зубьев в таком эквивалентном колесе

С увеличением угла β наклона линии зуба эквивалентные параметры возрастают, способствуя повышению прочности передач.
Зацепление косозубых колес отличается от зацепления прямозубых колес тем, что в каждом сечении, параллельном торцовой плоскости, фаза зацепления не одинакова.
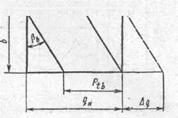
Линия контакта зубьев является также прямой, лежит в плоскости зацепления и наклонена к образующей основного цилиндра на угол βb (рис 20.17, tg βb = tg β cos αt). В результате возрастает длина линии контакта. Так, если в некоторый момент на одном торце зуба зацепление заканчивается (см. рис. 20.17), то для выхода из зацепления другого торца того же зуба линия контакта должна переместиться в положение, показанное штриховой прямой, на Δq=b tg βb .
Отношение εβ = Δq/pbt называют осевым коэффициентом перекрытия, а отношение εα = qα/pbt— торцовым коэффициентом перекрытия. Таким образом, коэффициент перекрытия косозубых колес
ε= εα + εβ.
|
Благодаря увеличению длины контактных линий (коэффициента перекрытия) косозубые колеса прочнее прямозубых,
работают плавно и менее шумно. Их целесообразно применять в быстроходных передачах.
Угол β наклона линии зуба назначают в пределах 8 — 20°, для шевронных колес β < 40°. Менее 8° угол β выполнять не следует, так как в этом случае утрачиваются указанные выше преимущества косозубых передач перед прямозубыми.
Рис. 20.17. Поле зацепления косозубого колеса
При увеличении угла β свыше 20° габариты опор становятся чрезмерно большими из-за возрастания осевой составляющей усилия в зацеплении.
Часто, например, в соосных передачах величину угла β наклона линии зуба устанавливают из условия размещения («вписывания») передачи в заданном межосевом расстоянии aw при фиксированных значениях иw, тn и z1. Тогда из формулы (20.14) следует

Значение угла β в заданных пределах при постоянных aw и и можно получить изменением z1 и тп.
Дата добавления: 2015-08-14; просмотров: 1132;
