ФРИКЦИОННЫЕ ПЕРЕДАЧИ И ВАРИАТОРЫ
§ 1. ВИДЫ МЕХАНИЗМОВ И ИХ НАЗНАЧЕНИЕ
Фрикционными передачами называют передачи трением. На рис. 19.1, а показана схема простейшей передачи, содержащей ведущий / и ведомый 2 катки, а также стойку 3 (несмещаемую опору) и ползун 4 (смещаемую под действием силы Fr опору).
Если к ведомому катку приложен момент сопротивления T2 (внешняя нагрузка), то для его преодоления требуется
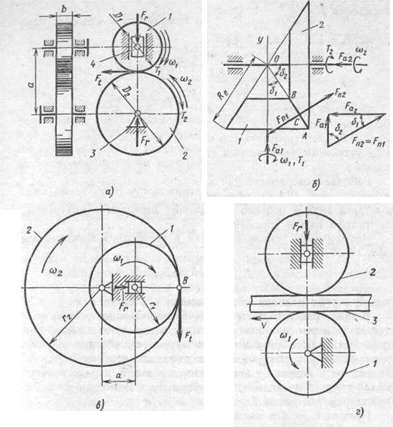
Рис. 19.1. Фрикционные механизмы
полезная окружная сила
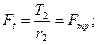 |
(19.1)
где r2 — радиус второго катка; FTP — сила трения, возникающая между контактирующими катками;
FTP = Fr f
здесь f — коэффициент трения качения, f = 0,05 — для пары роликов из стали или чугуна при работе в масле, f =0,1 ..0,15 — для пары сталь — текстолит или фибра без смазывания.
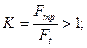 Для предотвращения проскальзывания в процессе работы (из-за износа, вибрации, перегрузки и т. д.) создают запас
Для предотвращения проскальзывания в процессе работы (из-за износа, вибрации, перегрузки и т. д.) создают запас
Сцепления . Обычно принимают в силовых пере-Ft
дачах К = 1,25 ..1,5, а в приборах - К = 3.
Отсюда необходимое усилие прижатия катков
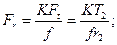 |
Обратим внимание, что усилие Fr оказывается существенно большим, чем сила Ft; например, при К = 1,25 и f = 0,05 Fr = 25 Ft. Это требует часто применения специальных нажимных устройств, увеличенных габаритов подшипников, жестких валов.
Рабочие поверхности тел качения могут быть также коническими (рис. 19.1,6), сферическими и др. Кроме внешнего контакта катков нередко используют передачи с внутренним контактом катков (рис. 19.1, в).
Необходимое усилие прижатия в конической передаче (см. рис. 19.1,6)
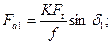 |
где δ1 — угол наклона образующей к оси катка.
В приборах (например, лентопротягивающих устройствах), транспортных машинах и др. используют механизмы (рис. 19.1, г), преобразующие вращательное движение ведущего звена-катка / в поступательное движение ведомого звена 3. Прижатие к ведущему звену ведомого может осуществляться силой тяжести последнего или, например, с помощью свободно вращающегося катка 2.
Прижатие катков является необходимым условием работы передач. Его осуществляют на практике либо постоянной силой, либо усилием, регулируемым при изменении внешней нагрузки. Постоянное прижатие получают за счет предварительной деформации при сборке упругих элементов системы (например, катков), использованием сил тяжести, установкой пружин (рис. 19.2). Регулируемое прижатие требует применения специальных нажимных устройств (винтовых, шариковых и др.), обеспечивающих Ft /Fr = const.
Механизмы описанных видов имеют постоянное передаточное отношение. Однако с помощью катков несложно образуется механизм с регулируемым передаточным отношением, называемый вариатором. На рис. 19.2, а показан лобовой вариатор, в котором ведущий каток 1 может перемещаться по своему валу (вдоль оси) в осевом направлении (как показано стрелками).
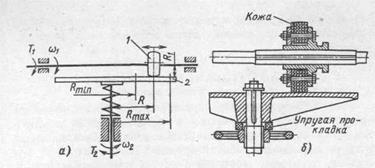
Рве. 19.2. Лобовой вариатор:
а — схема; б — сечение
стрелками). При этом передаточное отношение плавно изменяется по мере изменения радиуса R. Если каток 1 будет на «оси» катка 2, то последний не будет вращаться. При переводе катка 1 в левую часть катка 2 изменится направление вращения ведомого вала (реверсивное вращение).
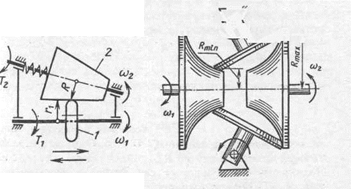
В вариаторе, показанном на рис. 19.3, изменение радиуса контакта ведомого звена с ведущим достигается за счет конической формы катка. На практике используют и другие виды вариаторов - торовые (рис. 19.4), клиноременные и др.
 Фрикционные передачи применяют в кинематических цепях приборов для обеспечения плавности движения, бесшумности и безударного включения. Фрикционные вариаторы применяют для обеспечения бесступенчатого регулирования скорости в станкостроении, текстильных, бумагоделательных и других машинах. Передаваемые мощности обычно составляют до 10 кВт. При больших мощностях трудно обеспечить необходимое усилие прижатия катков.
Фрикционные передачи применяют в кинематических цепях приборов для обеспечения плавности движения, бесшумности и безударного включения. Фрикционные вариаторы применяют для обеспечения бесступенчатого регулирования скорости в станкостроении, текстильных, бумагоделательных и других машинах. Передаваемые мощности обычно составляют до 10 кВт. При больших мощностях трудно обеспечить необходимое усилие прижатия катков.
| Рис. 19.3. Схема конусного вариатора Рис. 19.4. Торовый вариатор |
Основные недостатки передач: высокие нагрузки на валы от прижатия катков; износ катков и неизбежное проскальзывание.
§ 2. КИНЕМАТИКА И КПД ПЕРЕДАЧ
В нерегулируемой фрикционной передаче окружная скорость ведомого катка несколько меньше скорости ведущего катка из-за их взаимного проскальзывания, обусловленного упругими смещениями контактирующих точек катков и, как следствие, различием скоростей в точках площадки контакта. Обычно равенство скоростей («чистое» качение) имеет место лишь для точек катков, лежащих на линии начального контакта (контакта при Fr = О, см. рис. 19.1, а).
Влияние проскальзывания учитывают с помощью коэффициента ξ, определяемого опытным путем:
 |
Если ввести в рассмотрение угловые скорости ω1 и ω2 катков, то передаточное отношение
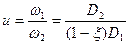
где ξ = 0,01 .. 0,05 — коэффициент скольжения.
Аналогично в передаче с коническими катками (см. рис. 19.1,6)
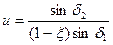 |
где δ1и δ2 — углы наклона к оси конусов образующих.
Для лобового вариатора (см. рис. 19.2) эта зависимость остается справедливой, и если пренебречь проскальзыванием, то
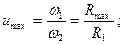 | 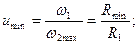 |
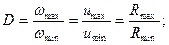 Диапазон регулирования
Диапазон регулирования
является одной из основных характеристик вариатора. Теоретически возможен случай Rmin= 0 и D →∞. Однако при малых R существенно возрастает скольжение и износ катков, снижается КПД, а потому практически диапазон регулирования ограничивают значением D ≤ 3.
Величина КПД передач и вариаторов зависит от потерь на скольжение и потерь в опорах валов, обычно η = 0,9 .. 0,95.
 § 3. РАСЧЕТ ПЕРЕДАЧ
§ 3. РАСЧЕТ ПЕРЕДАЧ
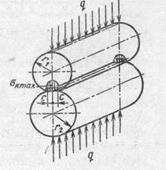
Виды повреждений катков. Рабочие поверхности металлических катков, работающих в масле при жидкостном трении, разрушаются из-за усталостного выкрашивания под действием переменных (от вращения) радиальных напряжений
сжатия σк в контактирующих точках (рис. 19.5). Существенно, что усилие прижатия вызывает неоднородную деформацию контактирующих точек по ширине площадки контакта и, как следствие, концентрацию контактных напряжений на линии центров катков. При действии вращающего момента T1 максимальное контактное напряжение σкmax смещается от оси центров на величину коэффициента трения f. Экспериментально установлено, что долговечность катков (число циклов нагружений до появления повреждений) пропорциональна максимальному напряжению σкmax.
| Рис. 19.5. Контактные напряжения в передаче |
В передачах, работающих без смазывания или при бедном смазывании, не обеспечивающем режима жидкостного трения, наблюдается изнашивание катков, также пропорциональное величине σкmax и коэффициенту трения f
Катки из неметаллических материалов разрушаются вследствие отслаивания рабочих поверхностей.
Расчет на прочность передачи. Расчет распределения напряжений в зоне контакта цилиндров впервые выполнен в конце XIX в. немецким механиком Г. Герцем. Он установил, что при коэффициентах Пауссона материалов цилиндров v1 и v2 максимальное напряжение в зоне контакта
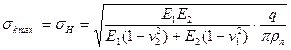 |
(19.3)
1 Здесь и далее в качестве индекса для максимальных напряжений в контакте используется латинская буква H — первая буква в немецкой записи фамилии Герца.
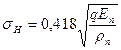 |
Если v1= v2 = 0,3, то
здесь q = Fr/b — распределенная нагрузка на цилиндры от усилия прижатия (Fr — радиальное усилие прижатия катков; b — длина катков); Eп и рп — соответственно приведенные модуль упругости и радиус кривизны цилиндров;
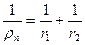
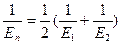 ;
;
где E1 и Е2 — модули упругости первого и второго катков; r1 и r2 радиусы катков. Знак плюс во второй формуле ставится при внешнем контакте катков, а знак минус — при внутреннем.
Так как контактная усталость передач существенно зависит от взаимного скольжения катков, а критерии контактной прочности не разработаны, то расчет передач ведут из условия прочности по допускаемым контактным напряжениям [σH], обобщающим предшествующий опыт эксплуатации (испытаний) фрикционных передач.
Вводя в рассмотрение передаточное отношение u = n1/n2 (n1 и n2 — частоты вращения катков), межосевое расстояние а = r1 + r2, коэффициент ширины катка ψ= b/а и выразив удельную нагрузку q через вращающий момент Т2 (см. формулу (19.2))у из условия прочности катков по допускаемым контактным напряжениям [σн] найдем соотношение для вычисления межосевого расстояния передачи

Значение [σн] принимают в зависимости от твердости по Бринеллю поверхности катков: для металлической пары при работе в масле [σн] = (2,5 .. 3) НВ, при работе всухую без смазочного материала [σн] = (1,2 .. 1,5) НВ. Для катков из текстолита при работе без масла принимают [σн] = = 80..100 МПа.
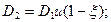
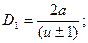 Диаметры катков
Диаметры катков
Далее определяют усилие прижатия Fr и нагрузки на валы и опоры.
ЗУБЧАТЫЕ МЕХАНИЗМЫ (ПЕРЕДАЧИ)
§ 1.ОБЩИЕ СВЕДЕНИЯ
Зубчатые механизмы (передачи) используют в большинстве машин и приборов для согласования движения в широком диапазоне мощностей (до 100 тыс. кВт) и скоростей (до 200 м/с); для передачи (с изменением угловой скорости и вращающего момента) вращательного движения и преобразования вращательного движения в поступательное (или наоборот). Они имеют высокий КПД (до 0,97 - 0,98 для одной пары колес — ступени), надежны в работе, компактны (малая масса) и просты в обслуживании.
Недостатки передач: необходимость изготовления с высокой точностью, шум при работе и др.
Передача движения в механизме реализуется с помощью зубчатых колес-дисков (цилиндров), снабженных чередующимися выступами и впадинами (рис. 20.1).
Передачу движения с помощью зубьев принято называть зубчатым зацеплением.
У зубчатого колеса условно различают тело и зубчатый венец, отделяемый от тела соосной поверхностью впадин (соосной называют поверхность вращения, ось которой совпадает с осью колеса).
Линия пересечения боковой поверхности зуба с какой-либо заданной поверхностью (например, плоскостью, перпендикулярной оси колеса, и т. п.) называется профилем зуба.
Колесо, радиус которого равен  бесконечности, называют зубчатой рейкой (см. рис. 20.1).
бесконечности, называют зубчатой рейкой (см. рис. 20.1).
| Рис. 20.1. Передача зубчатое колесо — рейка Рис. 20.2. Прямозубая цилиндрическая передача: а — схема; б — сечение |
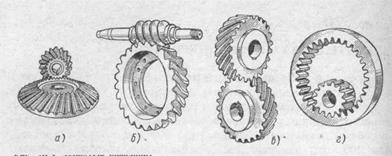 Рис. 20.3. Зубчатые передачи:
Рис. 20.3. Зубчатые передачи:
о — коническая; б —червячная; в —винтовая; г — цилиндрическая с внутренним зацеплением
Зубчатые передачи можно классифицировать.
1. По характеру движения осей:
а) обычные передачи, имеют неподвижные геометрические
центры (оси) всех колес;
б) планетарные передачи, центры одного или нескольких
колес подвижны.
2. По взаимному расположению осей:
а) цилиндрические передачи (передачи с параллельными осями, рис. 20.2);
б) конические передачи (передачи с пересекающимися осями, рис. 20.3, а);
в) гиперболоидные передачи (передачи с перекрещивающимися осями: червячные (рис. 20.3,6), винтовые (рис. 20.3, в), гипоидные и др.).
3. По относительному расположению поверхностей вершин и впадин зубьев колес:
а) передачи внешнего зацепления, образуются при зацеплении колес с внешними зубьями;
б) передачи внутреннего зацепления, образуются при зацеплении колес, одно из которых имеет внутренние зубья, а другое — внешние (рис. 20.3, г).
У колеса с внешними зубьями поверхность вершин находится вне поверхности впадин, а у колеса с внутренними зубьями — внутри поверхности впадин.
4. По направлению зубьев, оцениваемому по расположению
линии зубьев':
а) передачи с прямыми зубьями (прямозубые, см. рис. 20.2), имеют прямую линию зуба;
 1 Линией зуба называют линию пересечения боковой поверхности зуба с поверхностью, соосной (или однотипной) поверхности впадин.
1 Линией зуба называют линию пересечения боковой поверхности зуба с поверхностью, соосной (или однотипной) поверхности впадин.
б) передачи с винтовыми зубьями (рис. 20.3, в), линии которых на соосной поверхности являются винтовыми линиями любого вида.
Косые зубья являются разновидностью винтовых зубьев.
5. По профилям зубьев колес:
а) передачи с эвольвентным зацеплением, в котором профили зубьев являются эвольвентами окружностей;
б) передачи с циклоидальным зацеплением, в котором профили зубьев являются циклоидами;
в) передачи с зацеплением Новикова, в котором выпуклый профиль зуба одного колеса и вогнутый профиль зуба другого колеса очерчены дугами окружностей.
В зависимости от назначения зубчатые передачи могут встраиваться в конструкцию машины (встроенные передачи) или выделяться в самостоятельный узел (агрегат) и иметь отдельный корпус.
По конструктивному исполнению передачи могут быть расположены вне корпуса И иметь легкое ограждение (открытые передачи) либо в корпусе, изолирующем их от внешней среды (закрытые передачи). Открытые (как правило, прямозубые цилиндрические) передачи работают без смазывания или при ограниченном смазывании при небольших окружных скоростях (тихоходные передачи); закрытыми выполняют обычно передачи, работающие при средних и высоких окружных скоростях (быстроходные передачи) с обильным смазыванием (из масляной ванны, струей масла и др.).
Различают силовые и несиловые (кинематические) передачи. Силовые передачи используют для передачи мощностей и их габариты определяются, как правило, прочностной надежностью. Несиловые передачи выполняют в основном кинематические функции и мощности практически не передают. Размеры таких передач определяются конструктивными соображениями.
Зубчатые передачи могут понижать или повышать частоту вращения ведомого вала. В понижающей передаче частота вращения ведомого вала (колеса) меньше частоты вращения ведущего вала (колеса), а в повышающей передаче — больше.
Агрегат с понижающей передачей (передачами) называют редуктором, агрегат, с повышающей передачей — мультипликатором.
§ 2. КИНЕМАТИКА ЗУБЧАТЫХ ПЕРЕДАЧ
Основной кинематической характеристикой зубчатой передачи (рис. 20.4) является передаточное отношение

Рис. 20.4.Кинематическая схема двухступенчатой зубчатой передачи
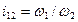 (20.1)
(20.1)
выражающее отношение угловых скоростей ω1 и ω2 колес при передаче движения от колеса 1 к колесу 2. При передаче движения от ведущего колеса к ведомому индекс 12 при i часто опускают.
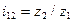 Зубья равномерно расположены на теле колеса и поворот ведущего колеса на один зуб вызывает поворот ведомого колеса тоже на один зуб. Несложно убедиться, что
Зубья равномерно расположены на теле колеса и поворот ведущего колеса на один зуб вызывает поворот ведомого колеса тоже на один зуб. Несложно убедиться, что
Отношение числа зубьев большего колеса к числу зубьев меньшего колеса (шестерни) называют передаточным числом и. Передаточное число либо равно передаточному отношению, либо является его обратной величиной.
По геометрическим и конструктивным соображениям желательно, чтобы колесо имело не меньше 10—13 зубьев и не больше 100—130 зубьев. При этом передаточное отношение зубчатой пары в среднем составит от 10 до 0,1. Если необходимо передаточное отношение, выходящее за эти пределы, применяют несколько последовательно расположенных зубчатых пар — ряд зубчатых колес.
Предположим, что требуется передать движение от вала 1 к валу 3 (см. рис. 20.4) с передаточным отношением, выходящим за пределы, допускаемые одной парой колес. Тогда, располагая между этими валами вал 2 и закрепляя на валах колеса z1 z2, z3 и z4, получим ряд зубчатых колес, состоящий из двух ступеней; z1 и z2 и z3 и z4.
Если угловая скорость вала 1 равна ω1, то угловая скорость вала 2
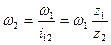 |
Угловая скорость вала 3
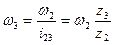 |
учетом этих равенств получим
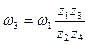 |
Таким образом, угловая скорость ведомого вала ряда равна угловой скорости ведущего вала, умноженной на дробь, в числителе которой произведение числа зубьев ведущих колес ступеней, а в знаменателе — произведение чисел зубьев ведомых колес.
Общее передаточное отношение ряда

(20.2)
равно произведению передаточных отношений отдельных пар колес (ступеней).
§ 3. ЭЛЕМЕНТЫ ТЕОРИИ ЗАЦЕПЛЕНИЯ ПЕРЕДАЧ
Рассмотрим передачу вращения двумя звеньями (рис. 20.5). Если предположить, что звенья 1 и 2 являются абсолютно твердыми (недеформируемыми) телами, то, действуя друг на друга в точке С контакта, они будут вращаться в противоположные стороны с угловыми скоростями ω1, и ω2. Найдем соотношение между этими скоростями.
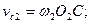
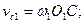 Окружные (линейные) скорости точки Сна каждом из звеньев
Окружные (линейные) скорости точки Сна каждом из звеньев
Проведем в точке С контакта нормаль п — п и касательную τ — τ к профилям звеньев и разложим скорости vcl и vc2 на нормальные и касательные составляющие.
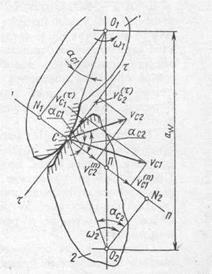 Тогда нормальные составляющие скоростей (см. рис. 20.5)
Тогда нормальные составляющие скоростей (см. рис. 20.5)
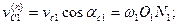 |
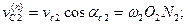 (20.3)
(20.3)
Рис. 20.5. Передача вращения двумя звеньями
где αCi- — угол между абсолютной скоростью точки контакта тела vCiи нормалью к профилю в этой же точке, численно равен углу между радиусом OiC и перпендикуляром OiNi опущенным из центра вращения звена Oi на нормаль п — п. Условие контакта тел будет обеспечено лишь при равенстве нормальных составляющих скоростей
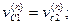 |
что вытекает из равенства координат сопряженных (имеющих общую внешнюю нормаль) точек контакта.
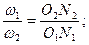 Последнее равенство с учетом зависимостей (20.3) дает
Последнее равенство с учетом зависимостей (20.3) дает
Если соединить прямой центры О1 и О2 и обозначить через П точку пересечения этой прямой с нормалью п — п, то из подобия полученных треугольников O1N1П и O2N2П следует, что
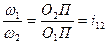 |
(20.4)
Зависимость (20.4) выражает собой основной закон зацепления: нормаль к профилям в точке контакта делит расстояние между центрами (межцентровое расстояние) на отрезки, обратно пропорциональные угловым скоростям звеньев. Существенно, что при постоянном передаточном отношении (i12 = const) и зафиксированных центрах О1 и О2 точка П будет занимать на линии центров неизменное положение. Отсюда или из равенства (20.4) следует, что для обеспечения постоянства передаточного отношения в процессе зацепления профили звеньев должны быть подобраны так, чтобы в любом положении профилей нормаль в точке их контакта пересекала бы линию центров в одной и той же точке П. Эта точка, таким образом, оказывается неподвижной в пространстве и называется ПОЛЮСОМ.
Теоретически один из профилей зубьев может быть выбран произвольно, но для обеспечения условия i12 = const форма профиля второго зуба должна быть вполне определенной. Профили зубьев, зацепление которых обеспечивает постоянное передаточное отношение, называют сопряженными.
Для реальных передач важно использовать профили наиболее технологичные и рациональные при изготовлении и в эксплуатации.
Одним из таких профилей является эвольеентный профиль, широко применяемый при изготовлении зубчатых колес.
Преимуществом эвольвентного зацепления, впервые предложенного Л. Эйлером, по сравнению с зацеплениями других видов (например, циклоидальным) является высокая технологичность:
а) эвольвентный профиль легче изготовить с высокой точностью, так как эвольвентные зубья могут быть обработаны инструментом с прямолинейной режущей кромкой;
б) эвольвентные профили нечувствительны к отклонениям межцентрового расстояния и поэтому не изменяют закона движения и передаточного отношения передачи.
Используют и другие виды зацеплений (циклоидальное, цевочное, часовое и т. д.). Среди «неэвольвентных» зацеплений наибольшее распространение получило зацепление Новикова (см. с. 337), характеризуемое высокой прочностью зубьев.
§ 4. ЭВОЛЬВЕНТНОЕЗАЦЕПЛЕНИЕ Основные сведения.Эвольвентой (от латинского слова evolvens) называют плоскую кривую, являющуюся разверткой другой плоской кривой, называемой эволютой. Для образования зубьев колес в качестве эволюты используют окружность, называемую основной (db — диаметр основной окружности). Эвольвенту этой окружности будет описывать любая точка прямой линии (производящей прямой), перекатываемой по ней без скольжения (рис. 20.6). Предельная точка М эвольвенты лежит на основной окружности. Используя известные из дифференциальной геометрии соотношения для определения
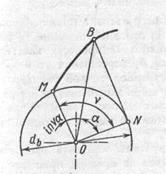
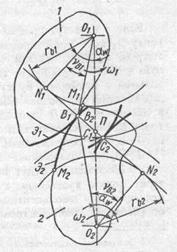
Рис. 20.6. К образованию эвольвентного профиля
 Рис. 20.7. Сопряженные профили
Рис. 20.7. Сопряженные профили
Дата добавления: 2015-08-14; просмотров: 2024;
