УСИЛИЯ И НАПРЯЖЕНИЯ В РЕМНЕ

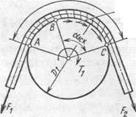
При движении ремень передает усилие с ведущего шкива на ведомый за счет сил сцепления (трения) на поверх­ностях контакта, определяемых углом α_i (i — номер шкива, i = 1,2) обхвата ремнем шкива (рис. 18.5). Для создания между ремнем и шкивами сил трения ремень прижимают к шкивам усилием предварительного натяжения F_o.

Под действием вращающего момента Т₁ в ведущей ветви (набегающей на ведущий шкив) передачи натяжение возрастет до некоторой величины F₁ вследствие появления момента сопротивления Т₂, а усилие в ведомой ветви (сбегающей с ведущего шкива) уменьшится до величины F₂.

При этом полезная нагрузка ремня (окружное усилие), равная силе трения между ремнем и шкивом, будет переда­ваться по всей дуге обхвата

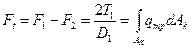
где q_тр — удельная сила трения; А_к — площадь поверхности контакта ремня со шкивом.

Если использовать модель ремня в виде гибкой нера­стяжимой нити, то усилия в ветвях передачи при действии рабочей нагрузки F, можно связать соотношением Л. Эйлера (см. с. 84), которое при учете центробежных сил примет вид

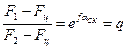где f— коэффициент трения между ремнем и шкивом; α_ск — угол дуги скольжения ремня по шкиву.

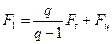
С учетом равенства (18.1) несложно найти

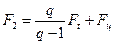откуда напряжения в сечениях веду­щей и ведомой ветвей ремня от начального натяжения

(18.3)

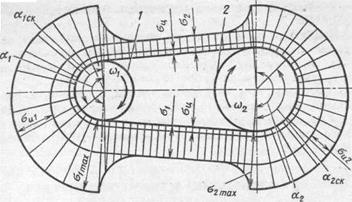
Рис. 18.6. Распределение напряжений в ремне передачи

и при действии внешней нагрузки

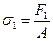
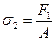(18,4)

где А — площадь поперечного сечения ремня.

Изменение напряжений вдоль ремня показано на рис. 18.6. Наибольшие напряжения испытывают наружные волокна в зоне контакта ремня с малым шкивом. Здесь к растягивающим напряжениям σ₁ от усилия натяжения F₁ добавляется на­пряжение растяжения от изгиба ремня (как стержня) вокруг шкива

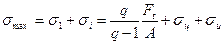(18.5)

Окружные растягивающие напряжения от центробежных сил находят, полагая, что ремень является кольцом, враща­ющимся со скоростью v (р — плотность материала ремня):

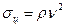(18.6)

Максимальные напряжения изгиба в ремне, как и в кольце, зависят от наименьшего диаметра D₁ шкива и толщины ремня h:

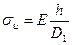(18,7)

где Е - приведенный модуль упругости ремня, для прорези­ненных ремней Е = 200 .. 300 МПа, для капроновых ремней Е = 600 МПа, для клиновых кордотканевых ремней Е = 500 ..600 МПа.

Напряжения σ₀ в ремне от начального натяжения наз­начают из условия обеспечения наибольшей долговечности ремня. На основании опыта эксплуатации передач с плоским и клиновым ремнем назначают σ₀= 1,2 ..1,8 МПа.

Существенно, что напряжения изгиба а σ_и являются переменными, они вызывают усталостное повреждение ремня.
Для уменьшения напряжений минимальное значение диаметра
малого шкива ограничивают [см. формулу (18.7)]. Обычно D₁/h=25..45

§ 3. КИНЕМАТИКА И ГЕОМЕТРИЯ ПЕРЕДАЧ

Скольжение в передаче. Работа упругого ремня сопровождается его неизбежным проскальзыванием, вызван­ным различным натяжением ведущей и ведомой ветвей и, как следствие, неравномерным распределением деформаций растяжения и сдвига по дуге обхвата. При обегании ремнем ведущего шкива натяжение его падает, ремень укорачи­вается и проскальзывает по шкиву. На ведомом шкиве ремень удлиняется, опережая шкив. Опытом установлено, что на первом участке АВ - дуге сцепления (см. рис. 18.5) за счет нарастающих тангенциальных сил сцепления (меньших полных сил трения) передается малая часть нагрузки, а де­формации сдвига ремня (показаны тонкими линиями) при­водят к небольшому относительному снижению его скорости.

В точке В силы сцепления становятся равными силам трения, происходит срыв и начинается скольжение ремня по дуге ВС — дуге скольжения. На этой дуге с углом α_ск за счет нарастающих от точки В к точке С сил трения передается основная часть окружного усилия и имеет место значительное снижение окружной скорости.

Снижение скорости от v₁ (для ведущей ветви) до v₂ (для ведомой ветви) характеризуют относительным скольже­нием

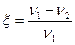Передаточное отношение

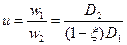В расчетах принимают ξ= 0,01 - 0,02.

Быстроходность передачи. Если окружные напряжения в рем­не, определяемые по формуле (18.6), σ_ц=σ₀ , то давление на всей дуге обхвата будет равно нулю, и передача не сможет передавать нагрузку. Окружная скорость на шкиве при этом

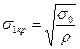Для ремня из капрона можно принять напряжение от начального натяжения σ₀= 50 МПа и v_1Kp = 150 м/с.

С увеличением быстроходности возрастают потери на тре­ние и при окружной скорости t)_Kp = |/ст_о/5р потери на трение будут наибольшими. Режимов работы передачи со скоростью v_2kp следует избегать из-за опасности перегрева ремня.

Оптимальная скорость ремней 20 — 25 м/с, а наибольшая допустимая 30 — 35 м/с. Узкие клиновые ремни с улучшенным кордом могут работать при скоростях до 40 — 60 м/с.

Геометрия передачи. Основными геометрическими парамет­рами передач являются диаметры шкивов D_t и D₂, межосевое расстояние а, длина ремня L и угол обхвата α на меньшем
шкиве. .

Для ограничения напряжений изгиба (см. с. 295) диаметр D_t меньшего шкива в клиноременной передаче регламентирован стандартом для каждого сечения ремня (ГОСТ 1284-80). Для передач с плоским ремнем минимальный диаметр (мм) меньшего шкива находят по эмпирической формуле

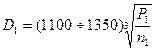где P₁ — передаваемая мощность, кВт; п₁— частота вращения меньшего шкива, об/мин.

Минимальное межосевое расстояние в плоскоременных пе­редачах

a_min = 0,5(D_l+D₂),

в клиноременных передачах (на основе данных эксплуатации) a_min = 0,55 (D_l+D₂) + h.

Для увеличения долговечности ремня принимают а > a_min.

Максимальное межосевое расстояние по экономическим соображениям (во избежание увеличения габаритов и сто­имости ремней) рекомендуют ограничивать величиной

а_max = 2(D₁+ D₂).

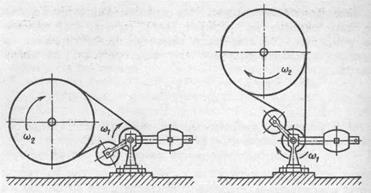
Рис. 18.7. Схема передач с натяжным роликом

Требуемая длина ремня для открытой передачи при за­данном (или желательном) межосевом расстоянии а и угле обхвата а определяется как сумма прямолинейных участков и дуг обхвата

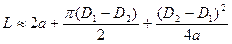Угол обхвата меньшего шкива

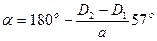Рекомендации по выбору а даны ниже. Длину для пере­дач с натяжным роликом (рис. 18.7) находят аналогично.

§ 4. ТЯГОВАЯ СПОСОБНОСТЬ И КПД ПЕРЕДАЧ

Прочность сцепления ремня со шкивом характери­зует тяговую способность передачи. Ее принято оценивать коэффициентом тяги — относительной нагрузкой в предполо­жении, что F_ц =0

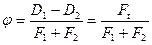С учетом равенства (18.2) несложно получить

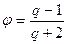Таким образом, коэффициент тяги зависит от условий работы передачи (угла обхвата, материалов ремня и шкива и др.).

Если положить, что при действии внешней нагрузки уд­линение ведущей ветви равно укорочению ведомой ветви, то получим (F_o — усилие начального натяжения ремня):

F₁=F₀ + 0,5F_t; F₂ = F_o - 0,5F_t, (18.8)

и соотношение для коэффициента тяги

φ= F_t/(2F₀).

Тяговую способность передачи удобно оценивать по вра­щающему моменту на ведущем (или ведомом) шкиве. Пре­небрегая силами инерции, из соотношений (18.1) - (18.2) и (18.8) найдем

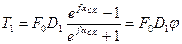Из этого равенства видно, что тяговая способность пере­дачи будет возрастать при увеличении предварительного на­тяжения ремня F_o, угла обхвата α и связанного с ним угла скольжения α_ск (в расчетах принимают α_ск ≈ 0,7α), а также коэффициента трения между ремнем и шкивами.

Для увеличения нагрузочной способности передачи необхо­димо стремиться к использованию более прочных ремней, допускающих высокие начальные напряжения (например, кап­рон, нейлон и др.). Однако в этом случае возрастают на­грузки на опоры.

Менее эффективно использование материалов с высоким ко­эффициентом трения в связи с возрастанием потерь на трение и опасностью перегрева ремня при упругом скольжении.

Нагрузочную способность передачи можно повысить, уве­личив коэффициент трения между ремнем и меньшим шкивом (для этого на меньший шкив надевают бандаж из специ­ально подобранного материала).

Для получения высокой тяговой способности передач с плоским ремнем рекомендуется обеспечивать α ≥150°.

В передачах с большим передаточным отношением и при малом расстоянии между осями валов угол обхвата для мало­го шкива и усилие натяжения часто увеличивают с помощью натяжных роликов (см. рис. 18.7), устанавливаемых на ведомой ветви.

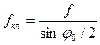Коэффициент трения / в последней формуле соответствует передаче с плоским ремнем. В клиноременной передаче

Для стандартных ремней φ₀ = 40° и f_кл ≈ 3f. Отсюда сле­дует, что в клиноременных передачах сцепление ремня со шкивом почти в 3 раза больше, чем в передаче с плоским ремнем. Благодаря этому клиноременные пере­дачи хорошо работают при углах обхвата α ≥120°. В ряде конструкций допускают α = 80..100°.

При работе плоскоременной передачи часть энергии рас­ходуется на упругий гистерезис при циклическом деформи­ровании ремня (растяжение, сдвиг, изгиб); на скольжение ремня по шкивам, аэродинамическое сопротивление движению ремня и шкивов, а также трение в подшипниках валов передачи.

В клиноременной передаче к этим потерям добавляются потери на трение при радиальном перемещении ремня в про­цессе входа его в канавку, и выхода из нее, а также воз­растают потери на упругий гистерезис при изгибе ремня (клиновой ремень имеет большую толщину, чем плоский ремень).

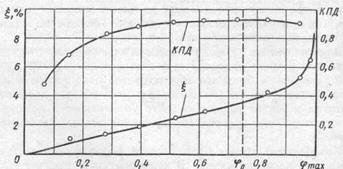
КПД ременной передачи зависит от коэффициента тяги φ и соответствующего ему относительного скольжения ремня ξ, (рис. 18.8). По мере увеличения относительной нагрузки до некоторого значения φ _о наблюдается линейное нараста­ние скольжения ремня от упругих деформаций, сопровож­даемое ростом КПД из-за уменьшения влияния потерь хо­лостого хода.

Дальнейшее увеличение ср приводит к более интенсивному снижению скорости, что связано с увеличением дуги сколь­жения и ростом потерь скорости при набегании ремня на шкивы.

Передача работает без буксования и в этой области, но КПД снижается из-за нарастания потерь энергии на трение. Лишь при φ = φ _mах начинается буксование.

Оптимальным считают нагружение передачи, соответствую­щее наибольшему КПД и некоторому запасу по сцеплению (φ _о = 0,4 .. 0,5 — для плоскоременных передач, φ _о = 0,6 .. 0,7 — для клиноременных передач).

При оптимальной нагрузке η = 0,97.. 0,98 для плоскоремен­ной передачи и η| = 0,92 .. 0,97 для клиноременной.