БАЛКИ НА УПРУГОМ ОСНОВАНИИ

Балки на упругом основании широко применяются в современных инженерных конструкциях различного назначения. Классификация данных балок включает как принимаемые условно за бесконечно длинные балки типа сварных рельсов, так и балки конечной длины.

В строительстве расчет многих типов фундаментов сводится к расчету балок на упругом основании. В транспортном строительстве к таким конструкциям относятся, например, водопропускные трубы, подводные тоннели на стадии их эксплуатации, а также различные виды трубопроводов.

В этой связи каждый инженер-строитель должен владеть методиками расчета балок на упругом основании. При этом следует учесть, что при реальном проектировании условия закрепления и загружения балок весьма разнообразны. Балки испытывают различные статические и динамические воздействия, а также воздействия осадок опор и температурных перепадов.

В настоящее время разработано значительное число методов расчета балок на упругом основании: метод конечных элементов (МКЭ), метод конечных разностей (МКР), вариационные методы, разновидности метода коллокаций, многие из которых позволяют решать реальные задачи проектирования с учетом переменных по длине жесткостей балки и упругого основания, а также работы основания за пределами балки.

Кроме того, при расчете балок на основании могут быть учтены нелинейные зависимости между напряжениями и деформациями как в материале балки, так и в основании под ней, что приближает расчет к реальной работе балки на нелинейном основании.

Однако для первоначального знакомства с методикой расчета балок на основании используются простейшие допущения об упругой работе материала балки и основания, о пропорциональной зависимости между прогибом балки и реактивным отпором упругого основания и об отсутствии воздействия на балку упругого основания за пределами балки.

При этом расчет балок на упругом основании осуществляется на основе теории, использующей аппарат дифференциального и интегрального исчисления, а получение численных результатов основано на использовании ПЭВМ.

Рассматриваются прямые стержни (балки), лежащие на сплошном упругом основании и находящиеся в условиях плоского поперечного изгиба, когда все внешние силы (нагрузки), реактивное давление основания и реакции опор лежат в плоскости, проходящей через одну из главных центральных осей инерции каждого поперечного сечения балки.

Предполагается, что способы определения положения этих осей студентам известны, поэтому этот этап расчета опускается и рассматриваются поперечные сечения, для которых положение по крайней мере одной из этих осей очевидно. К таковым относятся все сечения, имеющие по крайней мере одну ось симметрии, например, ось ОУ. В этом случае главная центральная ось совпадает с этой осью – рис. 1.

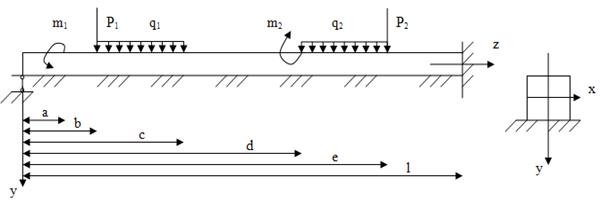
Рис. 1

Действующая на балку реальная нагрузка представляется в виде сосредоточенных сил 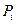(Кн), сосредоточенных моментов 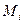(Кн м) и распределенных нагрузок 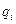(Кн/м), рис. 1.

По концам балки могут опираться различным образом: свободное опирание, рис. 2 а, б, при котором в ноль обращаются изгибающий момент М и поперечная сила Q, шарнирное опирание, рис. 2 в, г, при котором в ноль обращаются прогиб y и изгибающий момент М, защемление, рис. 2 д, е, при котором в ноль обращаются прогиб y и угол поворота сечения φ.

Рис. 2

СОСТАВЛЕНИЕ УРАВНЕНИЯ ПРОГИБОВ y (Z),

УГЛОВ ПОВОРОТА φ (Z), ИЗГИБАЮЩИХ МОМЕНТОВ М(Z)

И ПОПЕРЕЧНЫХ СИЛ Q(Z)

В соответствии с гипотезой проф. Винклера считаем деформацию упругого основания в каждой точке пропорциональной давлению в данной точке, поэтому реакция основания R (Z) получается пропорциональной прогибу балки y (Z) [1]:

R (Z) = K y(Z), (1)

где коэффициент пропорциональности К называется коэффициентом погонной жесткости упругого основания (“коэффициентом постели”) и измеряется в Паскалях (1 ПА = 1 н/м2); y (Z) – прогиб балки (м), R (Z) – реактивное погонное давление упругого основания (н/м). Коэффициент погонной жесткости упругого основания подсчитывается по формуле [3]:

K = K0 b, (2)

где К0 - коэффициент жесткости упругого основания, измеряемый в н/м3, b - ширина балки (м) в нижней ее части.

Дифференциальное уравнение изогнутой оси балки на упругом основании имеет вид [4]:

y(IV)+ 4 α4y = q (Z) / EI, (3)

где коэффициент α = 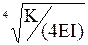(м-1), E - модуль упругости материала балки (Па), I - момент инерции сечения балки (м4), q (Z) – интенсивность поперечной нагрузки (н/м).

В соответствии с методом акад. А. Н. Крылова решение уравнения (3) записываем в виде [1]:

y (Z) = C1y1(αZ) + C2y2(αZ) + C3y3(αZ) + C4y4(αZ) + 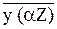. (4)

Здесь постоянные С1, С2, С3, С4определяются из условий закрепления балки по концам. Они связаны с начальными параметрами y0, φ0, M0, Q0, представляющими собой соответственно прогиб, угол поворота сечения, изгибающий момент, поперечную силу в сечении Z = 0 на левом конце балки, формулами [4]:

C1= y0, C2= φ0/ α, C3= - M0/ (E I α2), C4= - Q0/ (E I α3). (5)

В (4) функции y1, y2, y3, y4имеют вид [4]:

y1(αZ) = chαZ cosαZ, y2(αZ) = 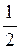(chαZ sinαZ + shαZ cosαZ), (6)

y3(αZ) = 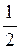shαZ sinαZ, y4(αZ) = 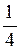(chα sinαZ – shαZ cosαZ).

Производные от функций y1, y2, y3, y4вычисляются по формулам:

(y1)́Z= -4α y4; (y2)́Z= α y1; (y3)́Z= α y2; (y4)́Z= α y3. (7)

Прогиб y (Z), угол поворота сечения φ (Z), изгибающий момент M (Z) и поперечная сила Q (Z) вычисляются по формулам:

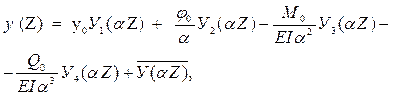(8)

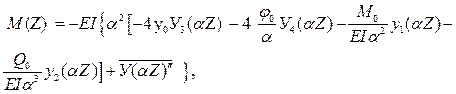
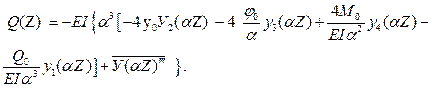
Частное решение 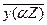в (8) имеет вид - рис. 3.

Рис. 3

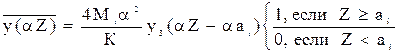, (9)

,

.

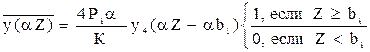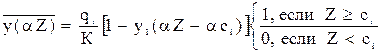Если приложенная к балке распределенная нагрузка qiне доходит до правого края балки, то ее условно продлевают до конца балки, а влияние этой добавки компенсируют той же нагрузкой с обратным знаком, рис. 4.

Рис. 4

При этом частное решение будет следующим:

. (10)

Отметим, что частное решение 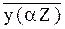может содержать несколько слагаемых, определяемых по формулам (9) и (10).

При составлении уравнений (8) используется следующее правило знаков для 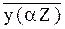: если внешний силовой фактор дает относительно данного сечения момент по часовой стрелке, то в уравнения (8) соответствующее слагаемое вводят со знаком минус.

Необходимо помнить, что при определении функций y (Z), φ (Z),

M (Z), Q (Z) в сечении Z = Ziучитываются лишь силы, расположенные слева от данного сечения.

Рассмотрим пример составления уравнений y (Z), φ (Z), M (Z), Q (Z) для балки, изображенной на рис. 5.

На балку, защемленную на левом конце и шарнирно опертую на правом, действует сосредоточенная сила Р в сечении “1” Z = 2 м, сосредоточенные моменты m1в сечении “2” Z = 4 м и m2в сечении “3” Z = 6 м, а также распределенная нагрузка q на участке от сечения “1” Z = 2 м до сечения “2” Z = 4 м.

Рис. 5

Возможно записать уравнения для y (Z), φ (Z), M (Z), Q (Z) для каждого характерного участка балки, то есть для участков 0-1, 1-2, 2-3, 3-4, рис. 5, но такая запись затруднительна при большом количестве характерных участков.

В этой связи записываем универсальные уравнения для y (Z), φ (Z), M (Z), Q (Z) для всей балки, включая в них индексы характерных сечений “1”, “2”, “3”, положение которых определяется приложенными силовыми факторами: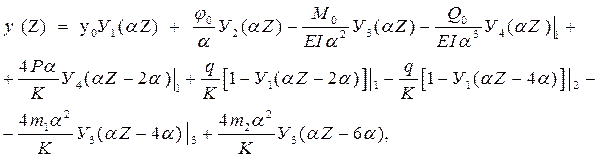

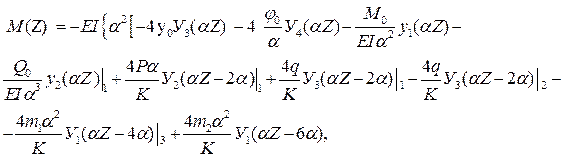9

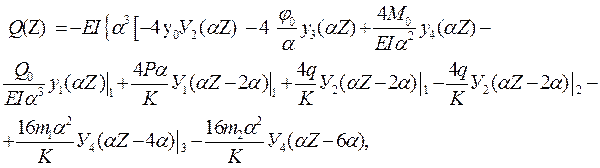
Индексы характерных сечений “1”, “2”, “3” в уравнениях ставятся непосредственно перед слагаемым, включающим силовой фактор, приложенный в конкретном характерном сечении балки. Данные индексы указывают, что стоящие за ними слагаемые учитываются, лишь начиная с данного характерного сечения.

В этой связи слагаемое, включающее момент m2, учитывается лишь для сечений с Z ≥ Z3= 6 м, слагаемое, включающее силу Р, учитывается лишь для сечений с Z ≥ Z2= 2 м, а слагаемое, учитывающее окончание участка с равномерно распределенной нагрузкой q, учитываются лишь для сечений с Z ≥ Z2= 4 м. Очевидно, что слагаемое, учитывающее момент m1, учитывается лишь для сечений с Z ≥ Z1= 4 м, а слагаемое, учитывающее нагрузку q, учитываются лишь для сечений с Z ≥ Z1= 2 м.

Например, в сечениях Z = 8 м, Z = 7 м учитываются все слагаемые в уравнениях, в сечении Z = 5 м не учитывается по одному последнему слагаемому, в сечении Z = 3 м – по три последних слагаемых в уравнениях. Очевидно, что в сечении Z = 1 учитываются лишь первые четыре слагаемых в уравнениях для y (Z), φ (Z), M (Z), Q (Z).