Лекция 13. Рассмотрим конкретную балку.

РАСЧЕТ ИЗГИБАЕМЫХ БАЛОК НА ПРОЧНОСТЬ

Рассмотрим конкретную балку.

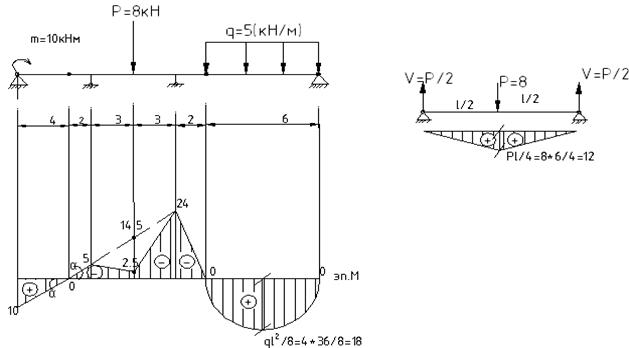
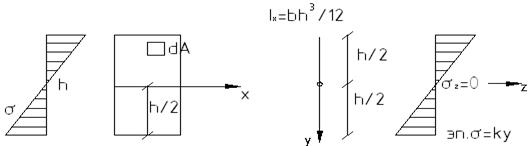
Выводим формулу для нормальных напряжений при изгибе. Из гипотез изгиба балок следует, что нормальное напряжение пропорционально вертикальной координате y: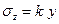

Изгибающий момент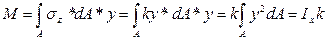

ð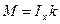

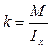
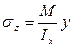- формула для нормального напряжения при изгибе.

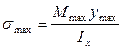
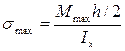
Вводим понятие момента сопротивления сечения при изгибе

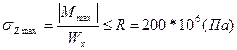
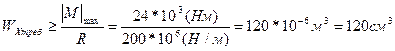
Для любого типа поперечного сечения балки должно быть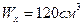

В ГОСТе имеется двутавр І №16 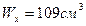,І №18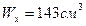

Проверим прочность I №16:

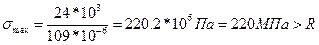
Перенапряжение составляет:

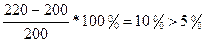-недопустимая величина перенапряжения

Возьмем I№18:

,

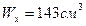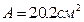
Рассмотрим балку из одного швеллера

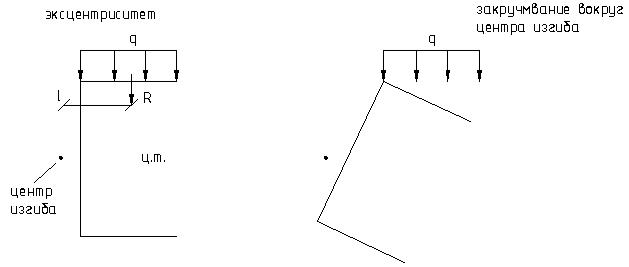
Необходимо изготовить сечение из 2-х швеллеров.

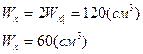
Берем швеллер [ №14:

,

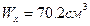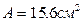
[] W_x=140.4см³, A_[]=31.2см²

Рассмотрим современное коробчатое сечение балки.

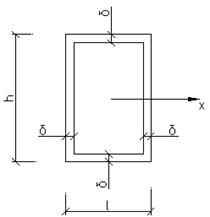
W_x=120см³

Для балок обычно принимается:

h=3b

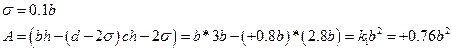
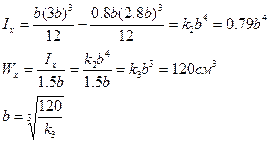
Рассмотрим кольцевое поперечное сечение балки (трубчатое)

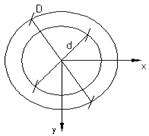
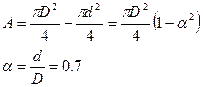
α-коэффициент тонкостенности

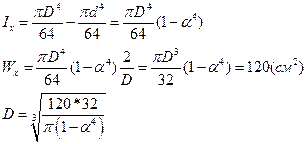
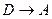
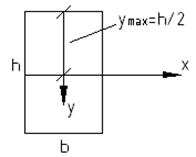
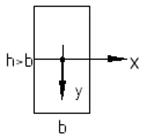
Рассмотрим прямоугольное поперечное сечение балки

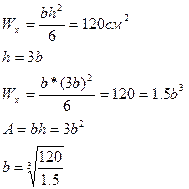
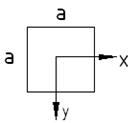
Рассмотрим квадратное поперечное сечение балки

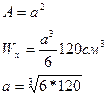
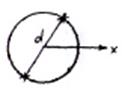
Рассмотрим круглое поперечное сечение балки

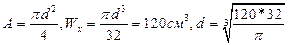
Сравниваем все типы поперечных сечений по расходу материала пропорционального площади поперечных сечений

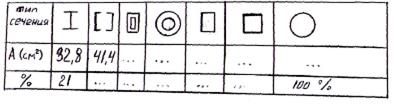
Рассмотрим вопрос о рациональности распределения материалов в различных типах поперечных сечений.

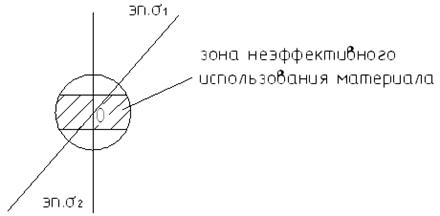
Нужно стремиться, чтобы в этой зоне было как можно меньше материала.

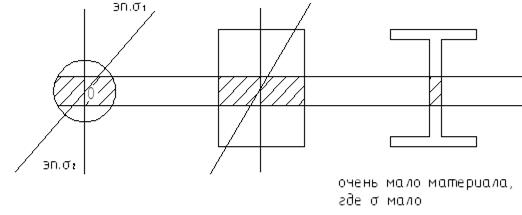
Таким образом, наиболее экономичны при изгибе балок те поперечные сечения, у которых материал максимально разнесен от нейтральной оси, вблизи от которой он используется неэффективно.