Лекция 10. Балкой называется как правило горизонтально расположенный прямолинейный стержень с определенным соотношением габаритов.

Изгиб балок

Балкой называется как правило горизонтально расположенный прямолинейный стержень с определенным соотношением габаритов.

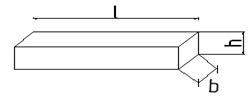
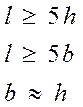
В сопротивлении материалов рассматриваются следующие опорные закрепления

балок: шарнирно-подвижная опора, шарнирно-неподвижная опора, заделка (жесткое защемление).

Нагрузки на балки делятся на: сосредоточенные силы P, сосредоточенные моменты M, распределенные по длине нагрузки q.

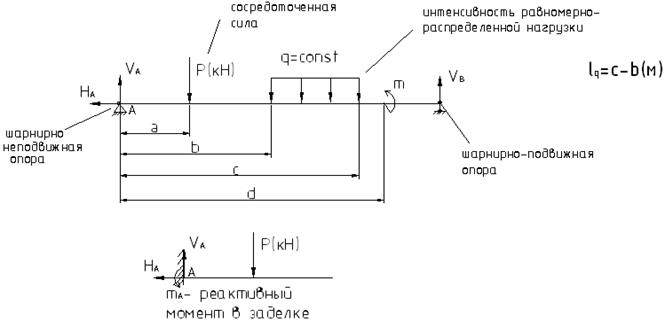
Проводим описание опытного исследования изгиба на образце балки.

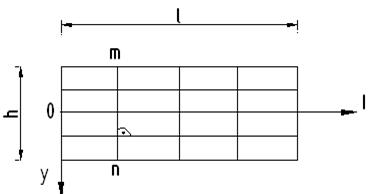
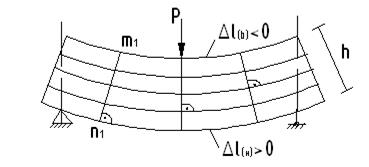
Из анализа деформированного состояния балки под нагрузкой можно установить следующее:

1. В процесса нагружения высоты балки остается постоянной

h=const

∆h=0

ε_y= ∆h/h=0

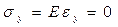(1)

Т.к. h=const, то волокна по высоте балки не давят друг на друга (гипотеза Навье)

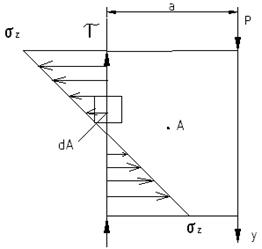
2. При изгибе рассматриваемой на рис. балки верхние волокна укорачиваются, нижние волокна удлиняются, а волокна посередине высоты прямоугольного поперечного сечения балки сохраняют свою длину (нейтральные волокна)

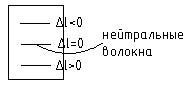
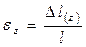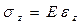, (2)

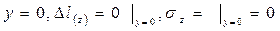(3)

ð На эпюре продольных нормальных напряжений на нейтральных волокнах балки

3.При изгибе балок нормальный элемент mnостается прямым и перпендикулярным к бывшим горизонтальным прямым.

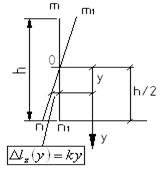
- прямая (линейная зависимость)

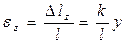
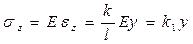- линейная зависимость

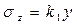По гипотезам Навье σ_zменяются по высоте сечения балки по линейному закону

\Из анализа формул (3) и (4) устанавливаем, что эпюра σ_zвыглядит следующим образом.

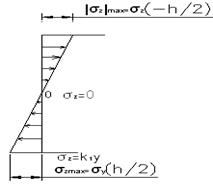
Вырежем из балки бесконечно малый элемент

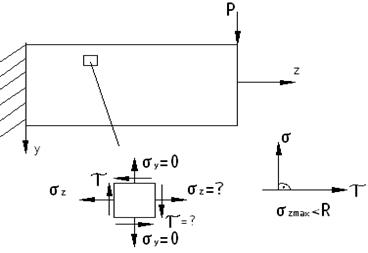
R_среза– расчетное сопротивление материала на срез.

Необходимо выявить внутренние силовые факторы в изгибаемой балке.

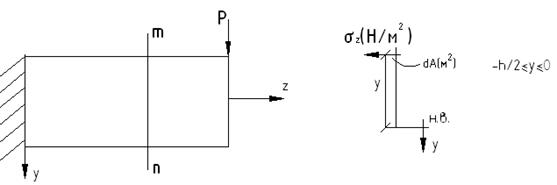
Используем метод сечений РОЗУ:

Условие несмещаемости по вертикали

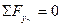
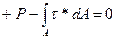
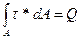- поперечная сила

,

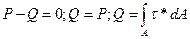то есть Q можно найти через внешние силы, приложенные к балке.

Определение (1): Поперечной (перерезывающей) силой Q(кН) в данном сечении балки называют внутренней силовой фактор 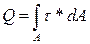, численно равный алгебраической сумме проекций на нормаль к оси балки всех сил, взятых по одну сторону от рассматриваемого сечения.

Правило знаков для поперечной силы Q:

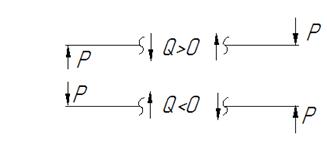
Q>0, если элемент балки вращается по часовой стрелке.

Рассмотрим пример подсчета Q.

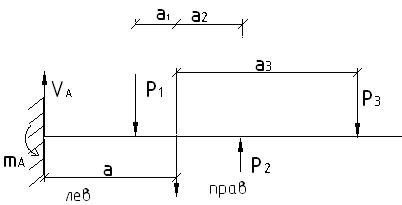
Рис. 1

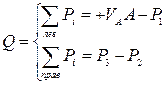
М_А не входит в уравнение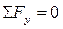

.

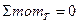Рассмотрим другой внутренний интегральный силовой фактор – изгибающий момент

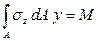- изгибающий момент

Итак, изгибающий момент может быть подсчитан двумя способами:

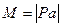
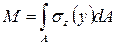
Определение (2): Изгибающим моментом M(z) (кН*м) в данном сечении балки называют внутренний силовой фактор 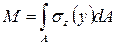, численно равный в данном сечении балки алгебраической сумме моментов всех сил, взятых по одну сторону от рассматриваемого сечения.

Правило знаков для изгибающего момента:

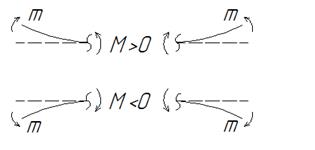
М>0, если при изгибе балки растягиваются нижние волокна

По рисунку (1) вычисляем момент:

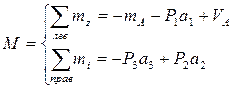
Существуют 9 фундаментальных правил взаимной проверки эпюр Qи M, основанные на теореме

Д.И. Журавского:

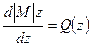(1)

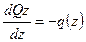(2)

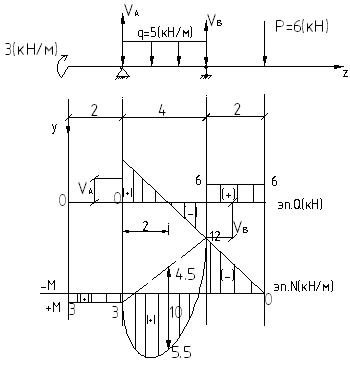
1. На участке балки без распределенной нагрузки q=0, Q=const, а момент меняется по закону прямой линии M=a+bz

2. На участке балки cраспределенной нагрузкой q=const, Q=a+bz- прямая, M=a₁+b₁z+c₁z² – парабола второй степени

3. если на участке балки Q_ij>0, то М_прав>M_лев

4. 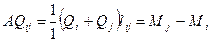- площадь эпюры Qна каждом участке балки равняется разности правой и левой ординат эпюры моментов Mна данной участке.

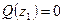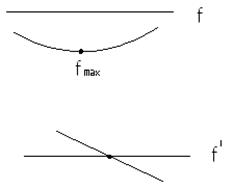
5. , 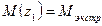- экстремальная ордината на эпюре М соответствует нулевому значению на эпюре Q

6.На эпюре Qпод каждой сосредоточенной силой реализуется скачок на величину данной силы по направлению данной силы

7. На эпюре М под каждым сосредоточенным моментом M_jреализуется скачок на величину М_j.

8. Если на эпюре изгибающих моментов +М – снизу, а –М – сверху, то направление распределенной нагрузки qуказывает направление выпуклости на эпюре М.

9. Направление каждой сосредоточенной силы Р_м указывает направление излома на эпюре М.