Лекция 5. Статически определимые и статически неопределимые задачи при растяжении и сжатии
Статически определимые и статически неопределимые задачи при растяжении и сжатии
В статически определимых задачах неизвестные находят из уравнений статики
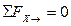
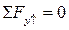
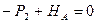
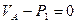
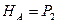
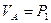
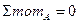

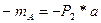
1) В статически неопределимых задачах уравнений статики недостаточно для нахождения неизвестных
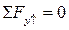
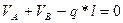 одно уравнение с 2-мя неизвестными
одно уравнение с 2-мя неизвестными
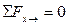
0=0
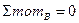
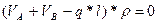
Необходимо записать 2-е уравнение из условия, что длина стержня L=const
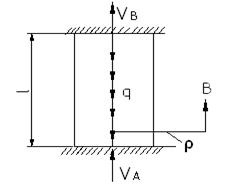
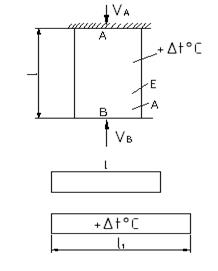
Рассмотрим температурную статически неопределимую задачу
При нагревании стержня он стремится расширится, однако этому препятствуют жесткие (несмещаемые) опоры
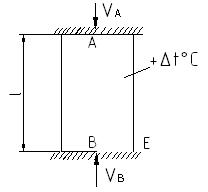
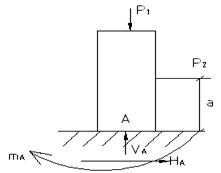
(1) Статическая сторона задачи:
Составим уравнения равновесия
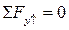
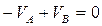 - одно уравнение с 2-мя неизвестными
- одно уравнение с 2-мя неизвестными
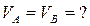
(2) Геометрическая сторона задачи:
l=const, т.е. расстояние между т. А и В остается постоянным
Используем метод сечений (РОЗУ)
Разрежем стержень сечением непосредственно у нижней опоры B
Отбрасываем нижнюю часть конструкции, т.е. опору В
Заменяем отброшенную опору В реакцией VB
Составляем уравнение 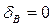
Которое соответствует отсутствию смещения т. В по вертикали:
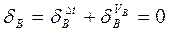
 ,
, 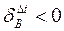
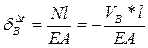
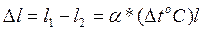 (1)
(1)
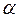 -коэффициент температурного расширения конкретного материала (1/град)
-коэффициент температурного расширения конкретного материала (1/град)
Для меди 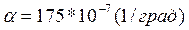
Для стали 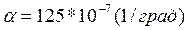
Для бетона 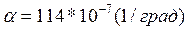
Возможность существования ж/б объясняется относительной близостью величин 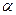 для стали и бетона
для стали и бетона
Подставляя полученные слагаемые в выражение для 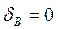 и получаем
и получаем
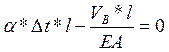
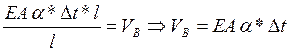
Рассмотрим конкретные значения: 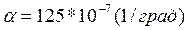
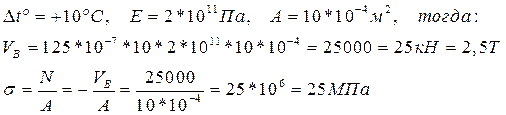
Итак, при решении задачи использовались:
1.Ур-е равновесия
2.Геометрические уравнения
3.З-н Гука (физическая сторона задачи)
Рассмотрим применение данного алгоритма к расчету следующей статически неопределимой системы:
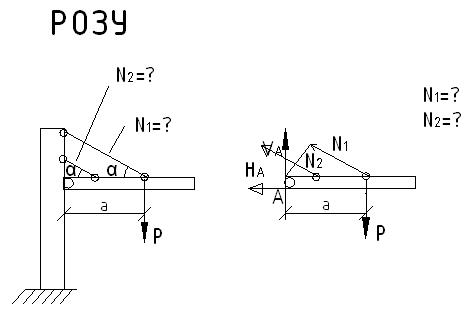
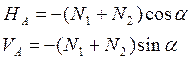
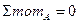 :
: 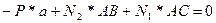 одно уравнение с 2-мя неизвестными
одно уравнение с 2-мя неизвестными
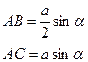
Для составления геометрического уравнения будем считать абсолютно жестким горизонтальный брус, который реально почти не изгибается при нагружении системы.
Изображаем деформированное состояние системы
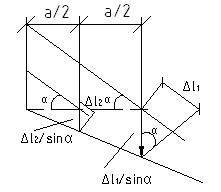
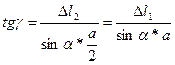 (2) -геометрическое уравнение
(2) -геометрическое уравнение
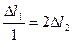
В геометрическое уравнение (2) не входят искомые усилия N1 и N2, поэтому необходимо
рассмотрение физической стороны задачи (уравнений закона Гука)
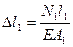
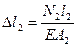 (3)
(3)
А1=А2=А
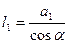 ,
, 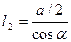
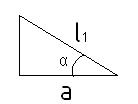
Подставляя данные формулы в уравнение (2)

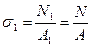
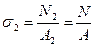
Рассмотрим пример статически неопределимой системы, когда усилие в одном из стержней является отрицательным
Вновь считает брус абсолютно жестким.
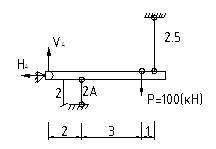
1) Уравнение статического равновесия
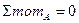 :
: 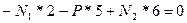 (1)
(1)
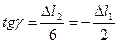 (2)
(2)
Данная запись необходима для того, чтобы в обоих частях равенства были положительные величины
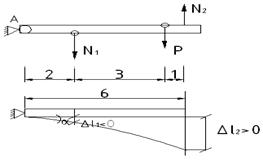
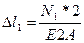 ,
, 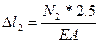 (3)
(3)
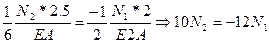
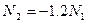
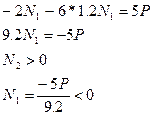
Дата добавления: 2015-08-01; просмотров: 646;
