Внецентренное сжатие стержней.

Рассмотрим стержень, подвернутый внецентреному сжатию.

Через L обозначаем эксцентриситет приложения сжимающей силы Р.

Внецентренно приложенную силу заменяем центрально приложенной силой и изгибающим моментом.

Рассмотрим реальное поперечное сечение стержня:

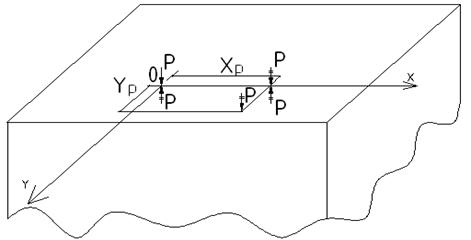
Рис. 1

Преобразует схему нагружения рассмотренным выше способом.

1)Переносим силу Р на ось ОХ: (у=0) и получаем следующий набор силовых факторов:

Р(х_р,0), М_х=Ру_р

2) Переносим силу Р в центральную точку О (0;0) и получаем следующий набор силовых факторов:

Р(0;0)- центральная сжимающая сила:

М_х=Ру_р- момент, относительно оси ОХ

М_у=Рх_р- момент, относительно оси OY

Запишем формулу для напряжений от действия 3-х выявленных силовых факторов:

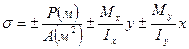(1)

Данная формула используется в общем случае внецентренного растяжения и сжатия.

Из знаков в формуле (1) в соответствии с конкретикой рис. 1 выбираем знаки “+” или “-“ перед каждым конкретным слагаемым:

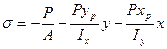(2)

Введем понятие о ГОСТотвских величинах радиусов инерции сечения: i_x, i_y (м)

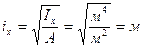- радиус инерции сечения относительно оси ОХ (м) (2,1)

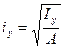- то же относительно оси OY (2,2)

Возведем формулу (2.1) в квадрат: ,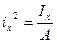

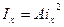(2,3)

Аналогично получаем выражение 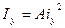(2,4)

Перепишем (2) в виде:

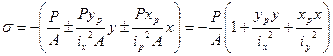(3)

Уравнения (2) и (3) представляют собой уравнения плоскости, не проходящей через начало координат, то есть при х=0, у=0 .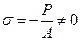

В некоторых случаях данная плоскость делит поперечное сечение на 2 части с разными знаками напряжения:

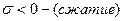: хорошо работают практически все материалы.

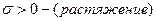: плохо работает кирпичная кладка и бетон. Например, для бетона класса 30

R_{бет сж} =30МПа

R_{бет раст} = 0.75МПа

Выводим формулу для нулевой линии, на которой напряжения равны нулю, т.е.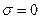

Из уравнения (3): 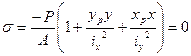, 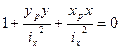(4)

В общем виде поиск нулевой линии по уравнению (4) сложен.

Найдем точку пересечения нулевой линии с осью Х, на которой Y=0:

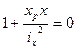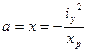, (5,1)

- найден отрезок, отсекаемый нулевой линией на оси ОХ.

Найдем точку пересечения нулевой линии с осью Y, на которой X=0:

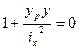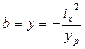, (5,2)

- найден отрезок, отсекаемый нулевой линией на оси ОY.

Пример: возьмем прямоугольное поперечное сечение

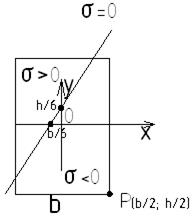
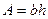
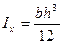
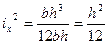
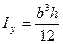
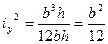
Определяем отрезки, отсекаемые нулевой линией на осях X и Y:

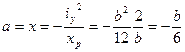- на оси OX

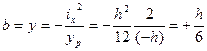- на оси OY

Если сила Р сменит свое положение, передвигаясь к центру тяжести сечения, то зона σ>0 будет прогрессивно убывать.

Классифицируем данные случаи:

1. нулевая линия пересекает контур сечения

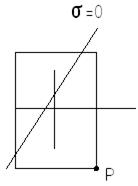
Рис. 2

В результате в сечении возникают как растягивающие, так и сжимающие напряжения.

2. нулевая линия касается контура сечения, при этом во всем сечении, кроме точки( точек) контура возникают напряжения одного знака.

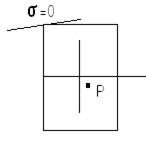
Рис.3

3. нулевая линия проходит вне контура сечения – во всех точках сечения, включая точки его контура, возникают напряжения одного знака.

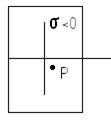
Рис. 4

Самым важным является случай 2, т.к. он является предельным для бетона, каменной складки и других материалов, плохо работающих на растяжение.

Вводим понятие об ядре сечения (специальной области вокруг центра тяжести сечения)

а) если сила Р расположена вне ядра сечения – нулевая линия (н.л.) пересекает контур сечения (рис.2)

б) если сила Р расположена на границе ядра сечения- нулевая линия касается контура сечения (рис.3)

Т.е. если привести нулевые линии, касающиеся контура сечения, то в этом случае мы найдем точки на границе ядра сечения.

Решим задачу:

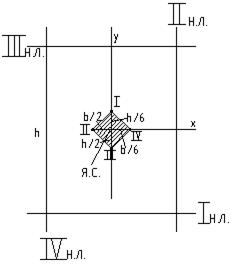
Рис. 5

І. Н.л. параллельна ОХ:

,

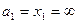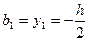
Перепишем формулы (5) в следующем виде:

,

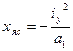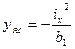
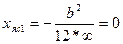: точка на границе ядра сечения имеет координату 0 на OY.

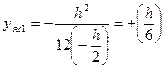
ІІ. Н.л. параллельна OY:

,

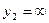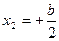
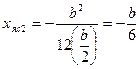
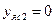- на OX

Справедлива следующая

Теорема: при вращении нулевой линии вокруг некоторой точки соответствующий ей центр давления перемещается по прямой.

Рассмотрим вопросы расчетов на прочность. Формула для напряжений при внецентренном сжатии имеет известный вид:

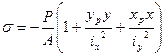
При знании положения н.л. можно выделить две характерные точки поперечного сечения – А и Р.

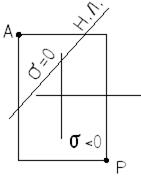
По закону плоскости максимальное напряжение будет в точке, наиболее удаленной от н.л.

Проводим расчет на прочность при сжатии:

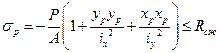
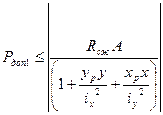
Проводим расчет на прочность при растяжении:

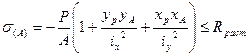
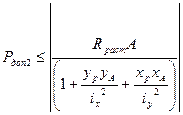
Из 2-х значений Р необходимо взять наименьшее, т.к. одновременно должны выполняться оба условия прочности (и на растяжение, и на сжатие).

Для построения эпюры нормальных напряжений на контуре поперечного сечения достаточно определить напряжения в точках излома контура и соединить их прямыми линиями, например: