Понятие ФКП
Глава 2. Функции комплексного переменного. Дифференцируемость и отображения
Понятие ФКП
Определение 14.Пусть дано некоторое множество М комплексных чисел z, например, некоторая область на плоскости Гаусса (z). Если каждому элементу z из этого множества по некоторому закону f поставлено в соответствие одно, вообще говоря, комплексное число ω = f(z), то говорят, что на множестве М определена функция комплексного переменного(ФКП) – ω.
ω = f(z)
Это определение однозначной функции. Если же каждому элементу z из этого множества по некоторому закону f поставлено в соответствие несколько значений ω, то функцию называют многозначной.
Область определения ФКП – множество М точек плоскости Гаусса (z).
Если каждая точка некоторого множества Е является значением функции ω = f(z), то говорят что Е – область значений данной функции или образ множества М. Функция ω = f(z) отображает М на Е.
Множество значений – также множество точек плоскости Гаусса, той же самой или, для удобства рассуждений, некоторой другой, но такой же плоскости Гаусса (ω).
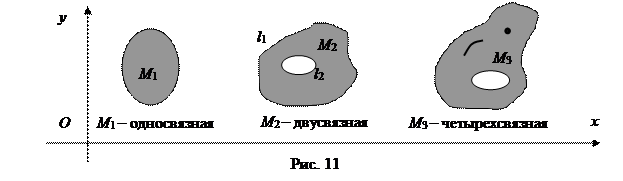
Определение 15.Область М (на плоскости, в пространстве) называется односвязной, если любой замкнутый контур, лежащий в этой области, можно непрерывно стянуть в точку, не выходя при этом за пределы области (иначе, область без «дырок»).
Например, область М,ограниченная замкнутой, не самопересекающейся линией называется односвязной. Если область М ограничена двумя замкнутыми не пересекающимися и не самопересекающимися линиями, то М называется двусвязной.
Если l1 – внешняя кривая, l2 – внутренняя кривая, ограничивающая область М, то М является двусвязной и в том случае, если l2 вырождается в точку или в дугу непрерывной линии. Аналогично могут быть определены трехсвязные, четырехсвязые и т.д. области (рис. 11).
В теории функций действительного переменного (ТФДП) изучаются функции, как отображения множеств евклидова пространства Еn в евклидово пространство Е1.
Замечание. Евклидово пространство – метрическое пространство, в котором для любых двух точек x и y определено число ρ(x, y) – расстояние от х до y или метрика так, что выполняются аксиомы:
1) ρ(x, y) = ρ(y, х),
2) ρ(x, y) > 0 при x 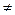 y; ρ(x, х) = 0 при любых х,
y; ρ(x, х) = 0 при любых х,
3) ρ(x, y) + ρ(y, z) 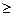 ρ(y, z).
ρ(y, z).
В ТФКП изучаются операторы, отображающие евклидово пространство Е2 в себя.
Определение 16.Закон преобразования функций – прообразов в функции – образы называется оператором.
Понятие оператора аналогично понятию функции, но если функция преобразует числа – значения независимого переменного в числа – значения зависимого переменного, то оператор преобразует функции в функции. Например, рассмотрим оператор дифференцирования D: D(f) = f ´. Тогда D(sin x) = cos x, где sin x – прообраз, cos x – образ.
Итак, ФКП – оператор отображения плоскости в себя или в другую плоскость.
Ни с каким иным геометрическим представлением ФКП не связана, кроме профиля модуля.
Определение 17. Профилем модуля функции в пространстве (x, y, N) называется поверхность  , каждая аппликата которой равняется модулю функции в данной точке z с координатами x, y плоскости Гаусса.
, каждая аппликата которой равняется модулю функции в данной точке z с координатами x, y плоскости Гаусса.
Рассмотрим комплексное число z = x + iy, тогда значение функции в точке z равно ω = f(z) – также комплексное число, а значит, как и всякое комплексное число, состоит из действительной и мнимой частей:
ω = f(z) = u + iv,
Re[f(z)] = u – действительная часть, Im[f(z)] = v – мнимая часть функции ω = f(z).
Таким образом, при переходе от точки z к точке z1 меняются координаты x и y на плоскости Гаусса, следовательно, меняется и значение f(z), т.е. изменяются u и v, следовательно, u и v тожефункции переменных x и y:
ω = f(z) = u(x, y) + iv(x, y).
Итак, ФКП определяется двумя функциями, каждая из которых в свою очередь есть действительная функция двух переменных.
Задача.Получить выражения для x, y через z и 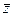 .
.
Дата добавления: 2015-07-14; просмотров: 1589;
