Нормальный закон распределения.
Опр:непрер СВ Х распределена по нормальному закону, если её плотность распр определена формулой 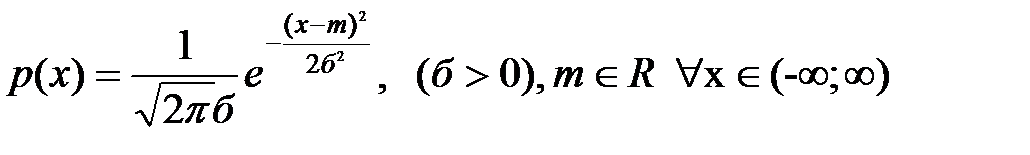
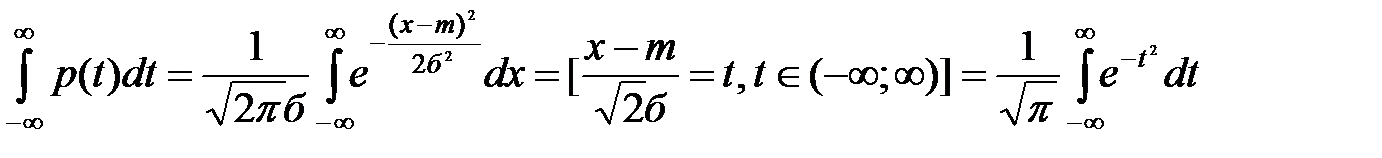
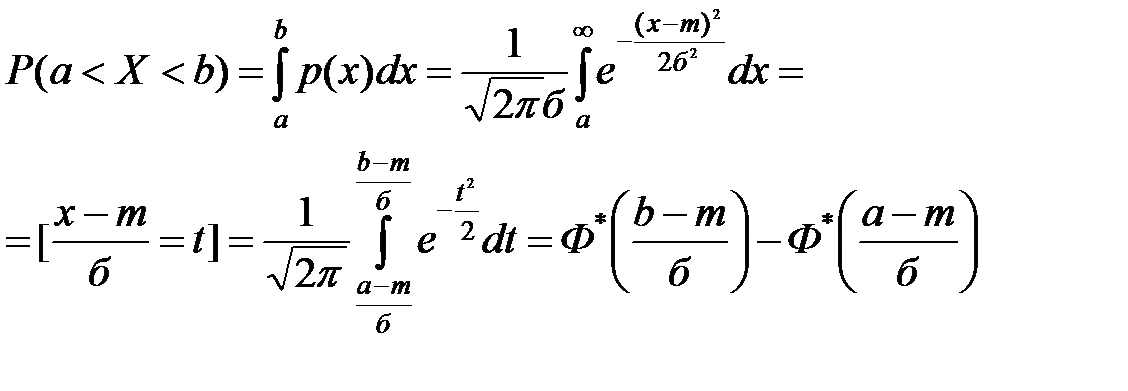
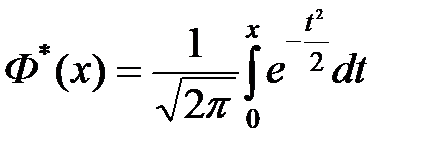
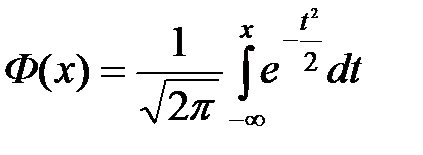
20.Многомерные случайные величины. Ф-ция распределения многомерной случайной величины, её свойства.
Пусть некоторый эксперимент описывается некоторыми случайными величинами 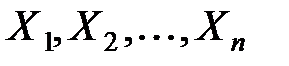 . Упорядоченный набор случайных величин (
. Упорядоченный набор случайных величин ( 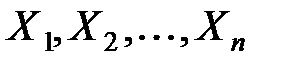 ) называется n-мерной СВ или n-мерным случайным вектором.
) называется n-мерной СВ или n-мерным случайным вектором. 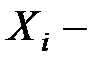 i-ая компонента данной СВ.
i-ая компонента данной СВ.
Пусть (Х,У) – двумерная СВ, множ значений которой состоит из изолированных точек 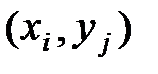 на плоскости. Такая СВ называется дискретной.
на плоскости. Такая СВ называется дискретной.
Перечень возможных значений пар компонент 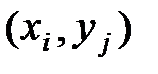 и соотв каждой такой паре вероятностей удовлетворяет условию
и соотв каждой такой паре вероятностей удовлетворяет условию 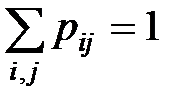 называется законом распределения дискретной СВ (Х,У).
называется законом распределения дискретной СВ (Х,У). 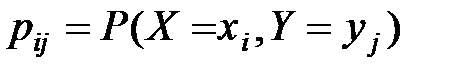
Одномерные законы распределения отдельных компонент выражаются через вероятности совм значений по формулам: 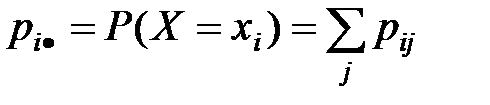
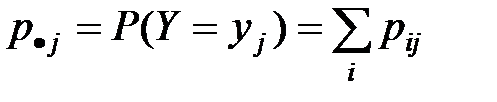 .
.
Распр дискр СВ
| Y X | 
| 
| … | 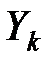
|
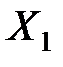
| 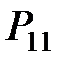
| 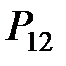
| … | |
| … | … | … | … | … |
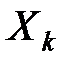
| 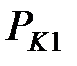
| 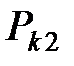
| … |
По аналогии можно определить распределение вероятностей n-мерной СВ.
Опр:ф-ция распр n-мерн СВ ( 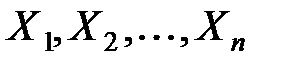 ) назыв ф-ция от n переменных
) назыв ф-ция от n переменных 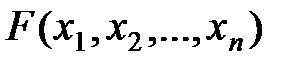 определенная во всем n-мерном евклидовом пр-ве формулой:
определенная во всем n-мерном евклидовом пр-ве формулой:
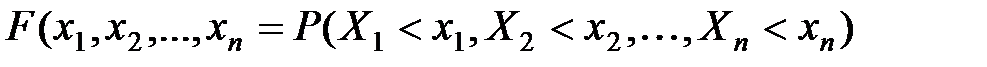 .
.
В частном случае для 2-х мерной СВ имеем: 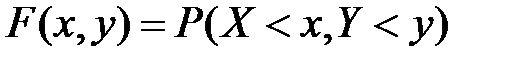
Ф-ция распр 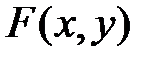 обладает следующ св-вами:
обладает следующ св-вами:
1. 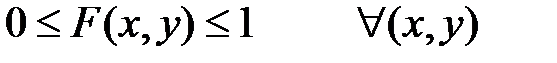
2. 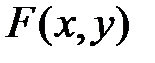 неубывающая ф-ция по каждому аргументу
неубывающая ф-ция по каждому аргументу
Док-во:ф-цияраспр 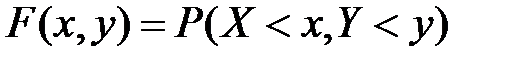 имеет следующ геометрич истолкование:
имеет следующ геометрич истолкование: 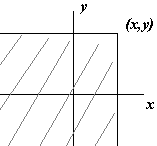
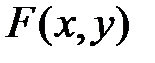 вероятность того, что случайная точка (Х,У) попадет в бесконечный квадрат с вершиной (х,у). Если смещать границу этого квадрата в сторону увеличения х или у, то вероятность попадания в этот квадрат случайной точки (Х,У) может только увеличиться.x
вероятность того, что случайная точка (Х,У) попадет в бесконечный квадрат с вершиной (х,у). Если смещать границу этого квадрата в сторону увеличения х или у, то вероятность попадания в этот квадрат случайной точки (Х,У) может только увеличиться.x
3. 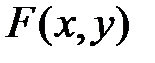 непрерывна слева по каждому из аргументов по каждой точке плоскости
непрерывна слева по каждому из аргументов по каждой точке плоскости
4. имеют место следующие предельные соотношения:
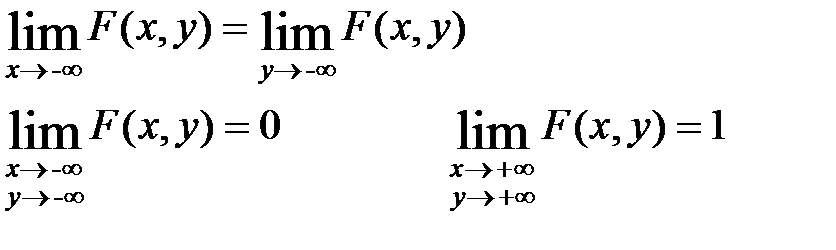
Док-во (одного из равенств): 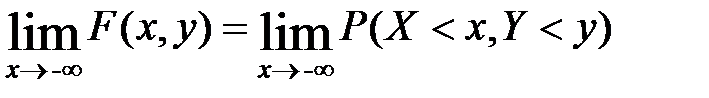 . Используя аксеому непрерывности вероятности получим:
. Используя аксеому непрерывности вероятности получим: 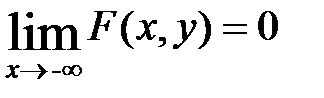 . x
. x
5. 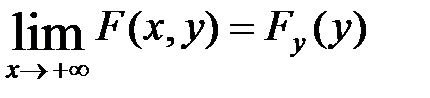 ,
, 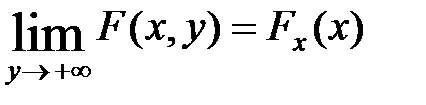 -одн-ные ф-ции распр велич
-одн-ные ф-ции распр велич
Док-во:отодвигаем одну из границ квадрата к 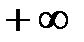 . При этом квадрат превращается в полуплоскость. Вероятность попадания случайной точки в такую полуплоскость есть ф-ция распре-деления соотв составляющей двумерной величины (Х,У). x
. При этом квадрат превращается в полуплоскость. Вероятность попадания случайной точки в такую полуплоскость есть ф-ция распре-деления соотв составляющей двумерной величины (Х,У). x
Для дискретной СВ ф-ция распр имеет вид:
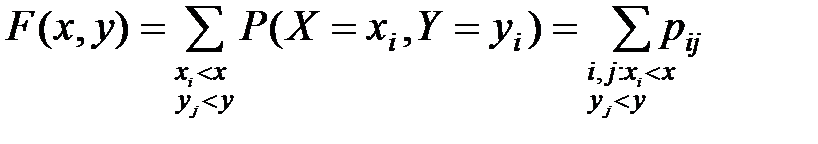
Св-ва 2-мерной СВ распространяются на n-мерные СВ.
21. Двумерные непрерывные СВ. Плотность распределения вероятностей двумерной СВ, её свойства
Опр:2-мерная СВ назыв непрерывн СВ, если ее ф-ция распр 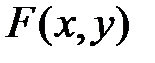 непрерывна на всей плоскости и сущ такая неотрицат интегрируемая по Римману в бесконечных пределах по каждой из координат ф-ция
непрерывна на всей плоскости и сущ такая неотрицат интегрируемая по Римману в бесконечных пределах по каждой из координат ф-ция 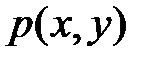 , такая, что
, такая, что 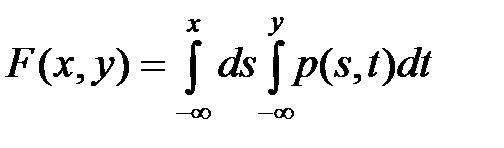
Ф-ция 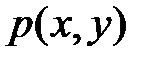 назыв плотностью распределения СВ (Х,У).
назыв плотностью распределения СВ (Х,У).
Св-ва плотности: 1. 
2. 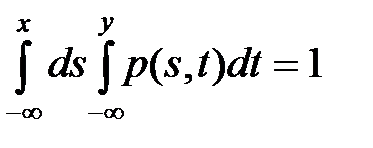
3.если (х,у) точка непрерывности плотности 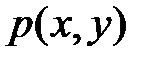 , то
, то 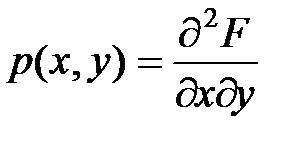
4.плотности распределения вероятностей отдельных компонент СВ (Х,У) выражается следующ образом через 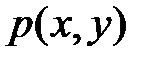 :
: 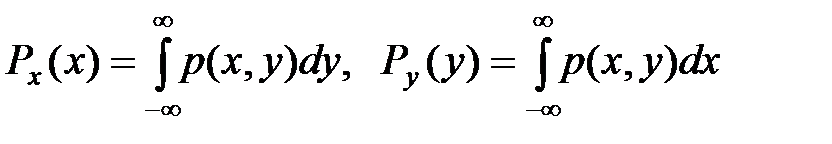
5.если (Х,У) непрер СВ, то вероятн попадания случайной точки в произвольный квадрат области G на плоскости определяется по формуле: 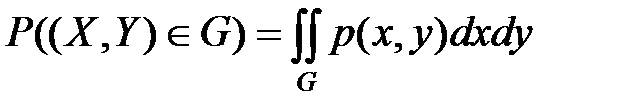 .
.
Вероятностный смысл плотности распределения
Пусть 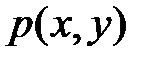 непрерывна в окрестности точки (х,у).
непрерывна в окрестности точки (х,у). 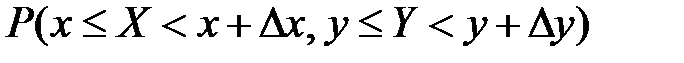
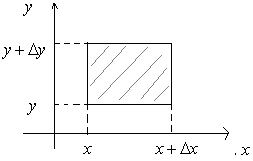
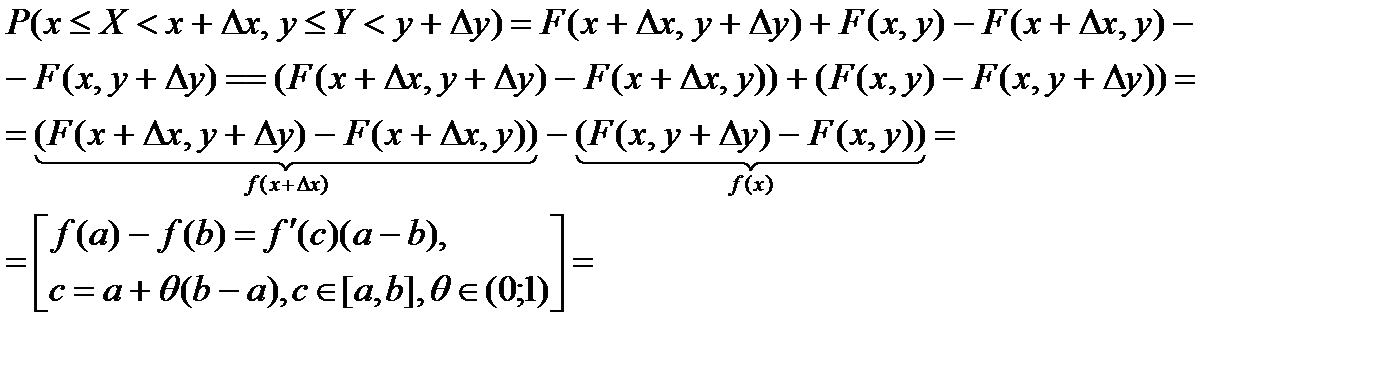
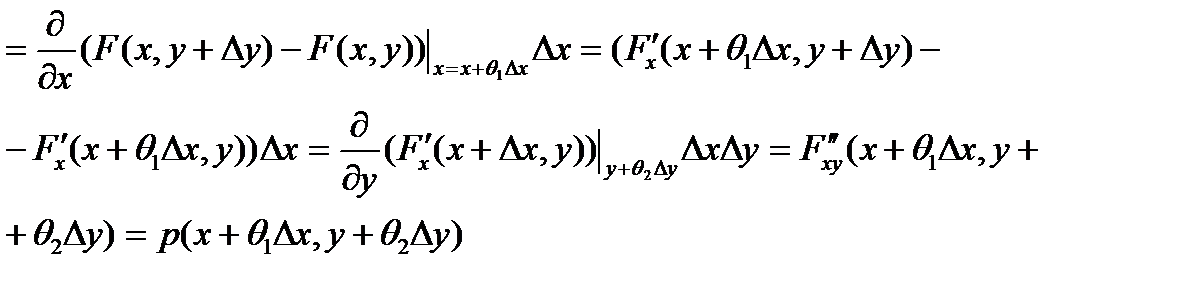
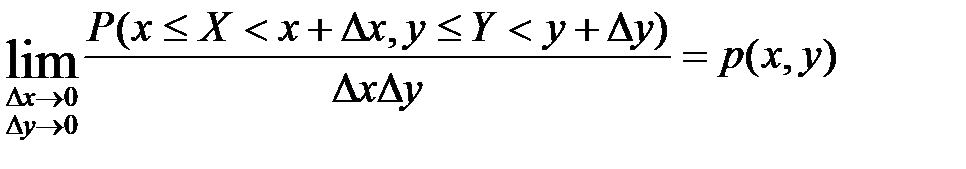
Т.о плотность распределения вероятностей 2-метной СВ (Х,У) можно рассматривать как предел отношения вероятности попадания СВ (Х,У) в прямоугольник со сторонами 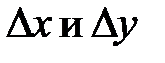 к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к 0 по длине.
к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к 0 по длине.
Из полученной формулы следует, что 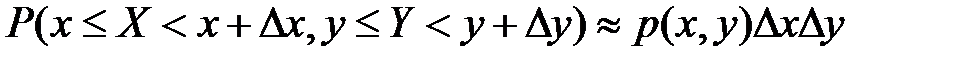
С точностью до бесконечно малых высшего порядка чем 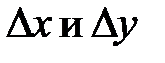 .
.
Дата добавления: 2015-06-27; просмотров: 967;
