Функции случайных величин, их законы распределения.

Опр:пусть дана ф-ция одной переменной с областью определения D(f), и пусть дана некоторая СВ Х все значения которой принадлежат D(f). Тогда, если Х приняла значение х, будем считать, что новая СВ У приняла значение f(x). Эта новая СВ называется ф-цией СВ Х. В этом случае записываем: Y=f(X).

I. Выясним как найти распределение ф-ции одной СВ по известному распределению дискретного аргумента.

а)если различным возможным значениям аргумента Х соответствуют различные возможные значения ф-ции У, то вероятности соответствующих значений Х и У между собой равны: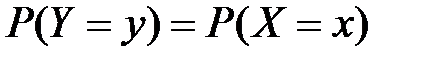

б)еслиразличным возможным значениям Х соотв значения У, среди которых есть равные между собой, то следует складывать вероятности повторяющихся вероятностей: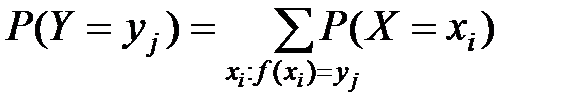

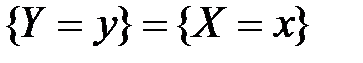
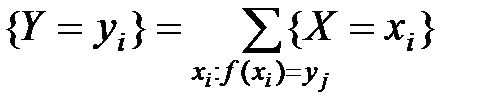
II.Та же задача ставится и для непрерывного аргумента: имеется плотность распределения СВ – р(х), а через нее хотим выразить .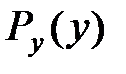

Теорема:если f(x) дифференцируемая строго возрастающая ил строго убывающая ф-ция, обратная ф-ция которой 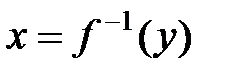, то имеет место равенство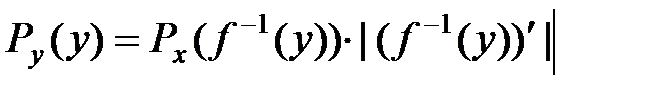

Док-во:пусть 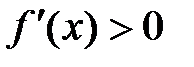и пусть множество значений СВ А это отрезок [a,b].

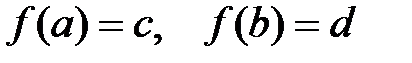
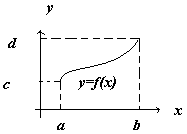
Ф-ция распределения СВ Y=f(X) имеет вид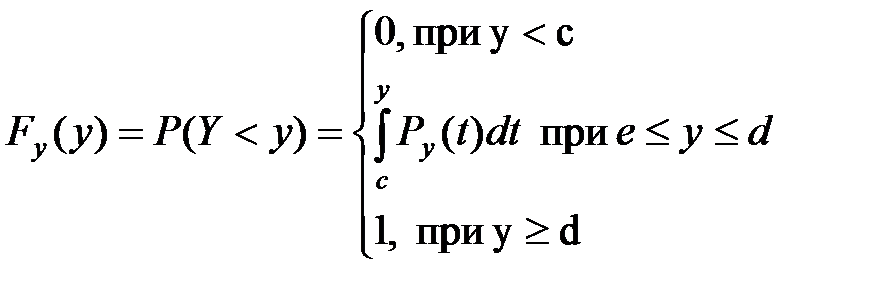

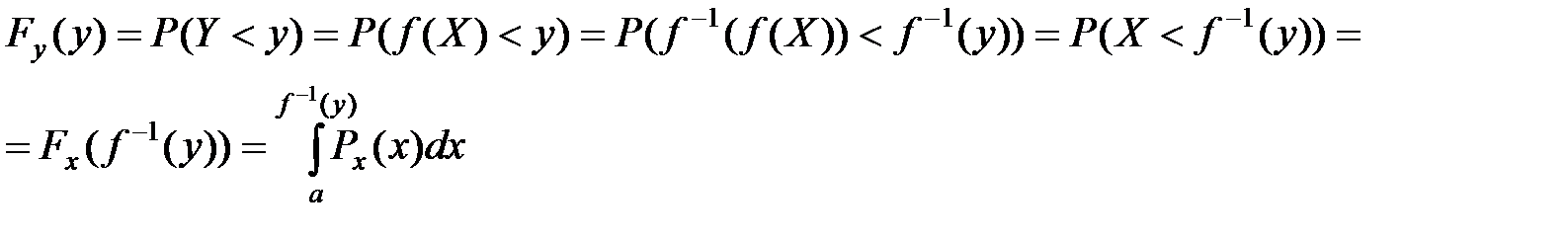
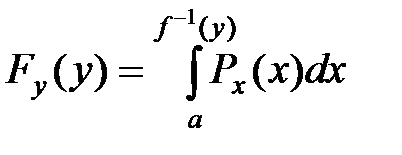
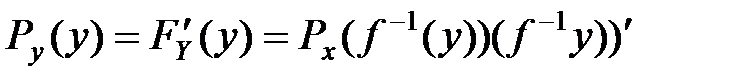
f(x) - возрастает 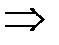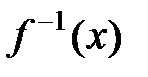возрастает 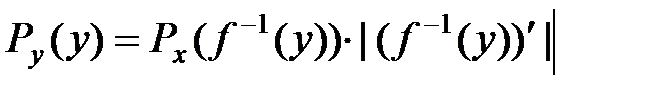x

Замечание:можно рассматривать также ф-ции от 2 и более случайных величин